Example 3 - Areas of Parallelograms and Triangles

Last updated at Dec. 13, 2024 by

Example 3 - Show that median of a triangle divides it - Median divides triangle into two triangles of equal area

Example 3 - Chapter 9 Class 9 Areas of Parallelograms and Triangles - Part 2

Go Ad-free

Transcript

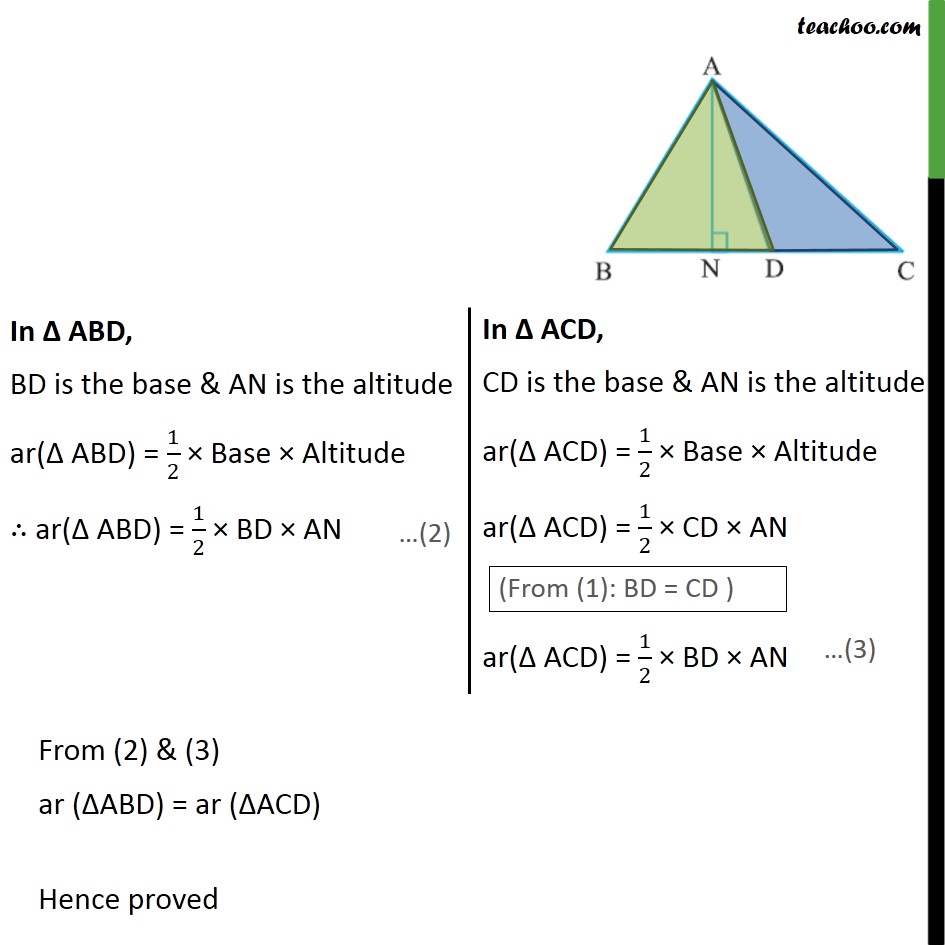
Example 3 Show that median of a triangle divides it into two triangles of equal area Given: A ABC with AD as the median BD = CD = 1/2 BC To prove: ar ( ABD) = ar ( ACD) Construction: Draw line AN BC Proof: To find area , we use formula Area of triangle = 1/2 Base Altitude From (2) & (3) ar ( ABD) = ar ( ACD) Hence proved

Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. He provides courses for Maths, Science and Computer Science at Teachoo