Check sibling questions

Question 1 - Ex 8.2 - Chapter 8 Class 9 Quadrilaterals

Last updated at May 29, 2023 by

Ex 8.2, 6 - Show that the line segments joining mid-points - Ex 8.2

Ex 8.2, 6 - Chapter 8 Class 9 Quadrilaterals - Part 2
Ex 8.2, 6 - Chapter 8 Class 9 Quadrilaterals - Part 3

Learn in your speed, with individual attention - Teachoo Maths 1-on-1 Class

Book a free demo

Transcript

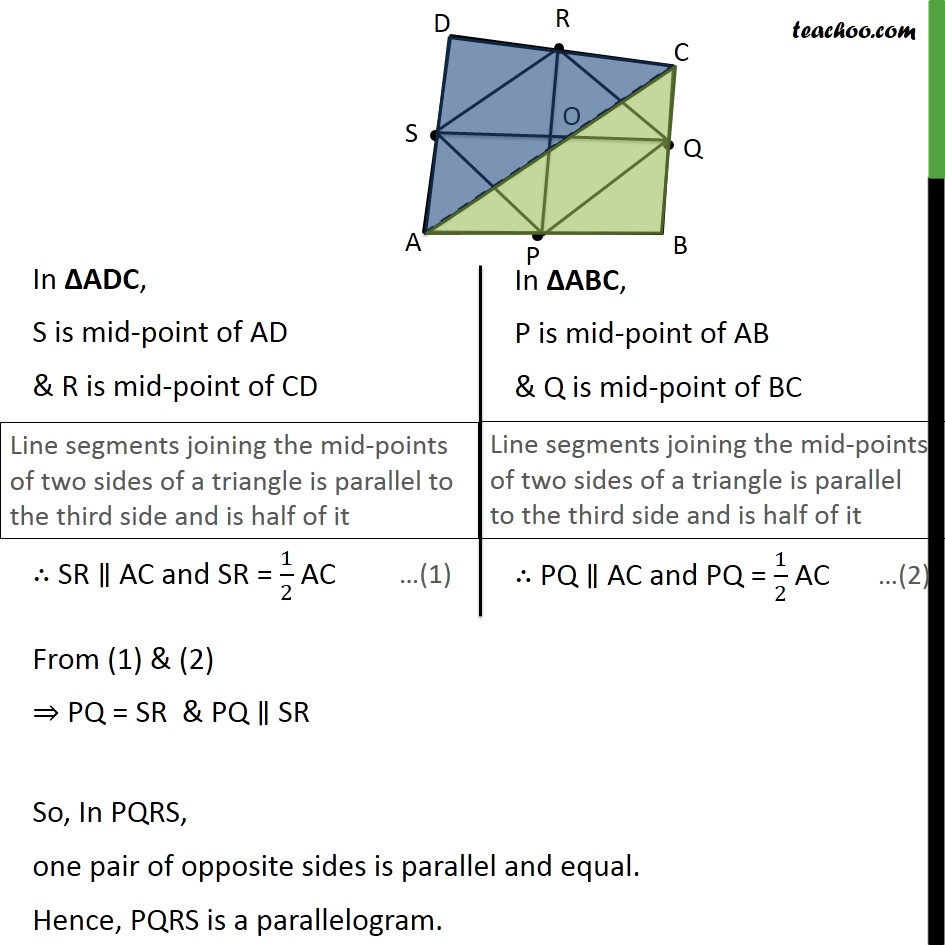
Ex 8.2, 6 Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other. Given: Let ABCD is a quadrilateral P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively To prove: PR & SQ bisect each other i.e. OP = OR & OQ = OS Construction: Join A & C Proof: PR & SQ are diagonals of parallelogram PQRS So, OP = OR & OQ = OS Hence proved

Ask a doubt
Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 13 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.