

Last updated at Feb. 27, 2025 by Teachoo



Transcript
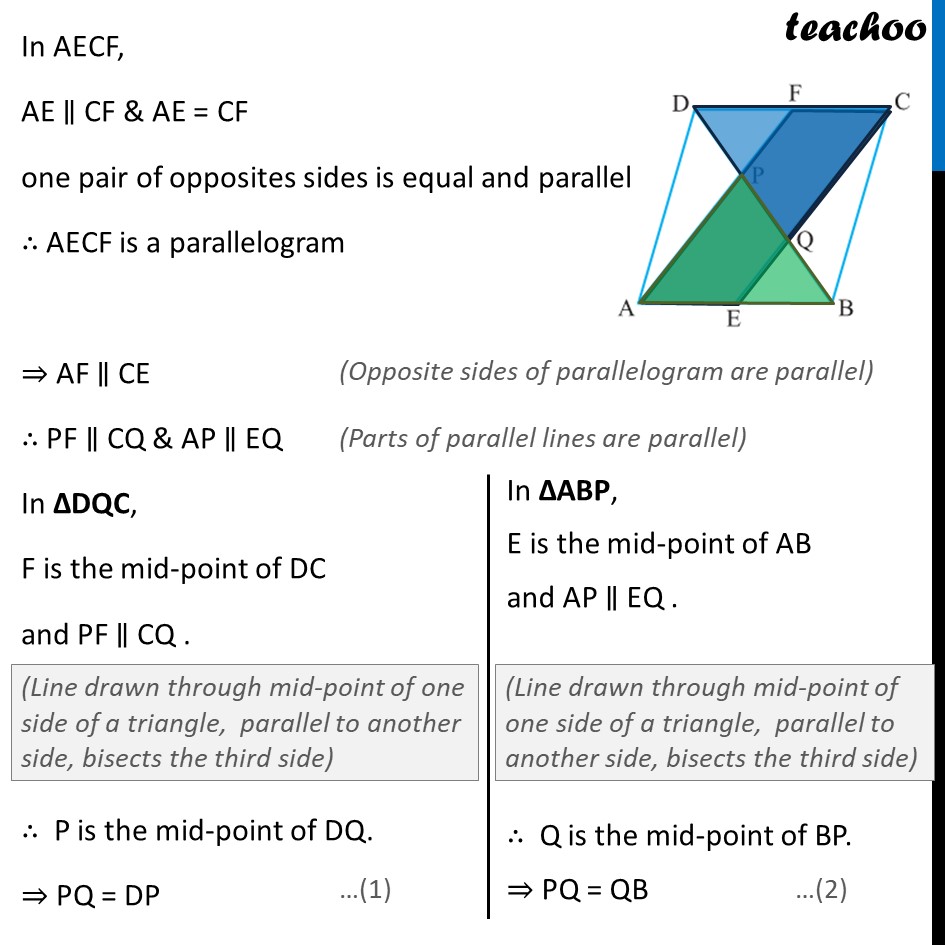
Ex 8.2, 5 In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively. Show that the line segments AF and EC trisect the diagonal BD. Given: ABCD is a parallelogram where E and F are the mid-points of sides AB and CD respectively To prove: AF & EC trisect BD i.e. BQ = QP = DP Proof: ABCD is a parallelogram. ∴ AB ∥ CD ⇒ AE ∥ CF & AB = CD 1/2 AB = 1/2 CD ∴ AE = CF In AECF, AE ∥ CF & AE = CF one pair of opposites sides is equal and parallel ∴ AECF is a parallelogram ⇒ AF ∥ CE ∴ PF ∥ CQ & AP ∥ EQ In ΔDQC, F is the mid-point of DC and PF ∥ CQ . ∴ P is the mid-point of DQ. ⇒ PQ = DP From (1) & (2) DP = PQ = BQ Hence, the line segments AF and EC trisect the diagonal BD. Hence proved