

Finding Area of Polygons
Last updated at Dec. 16, 2024 by Teachoo








Transcript
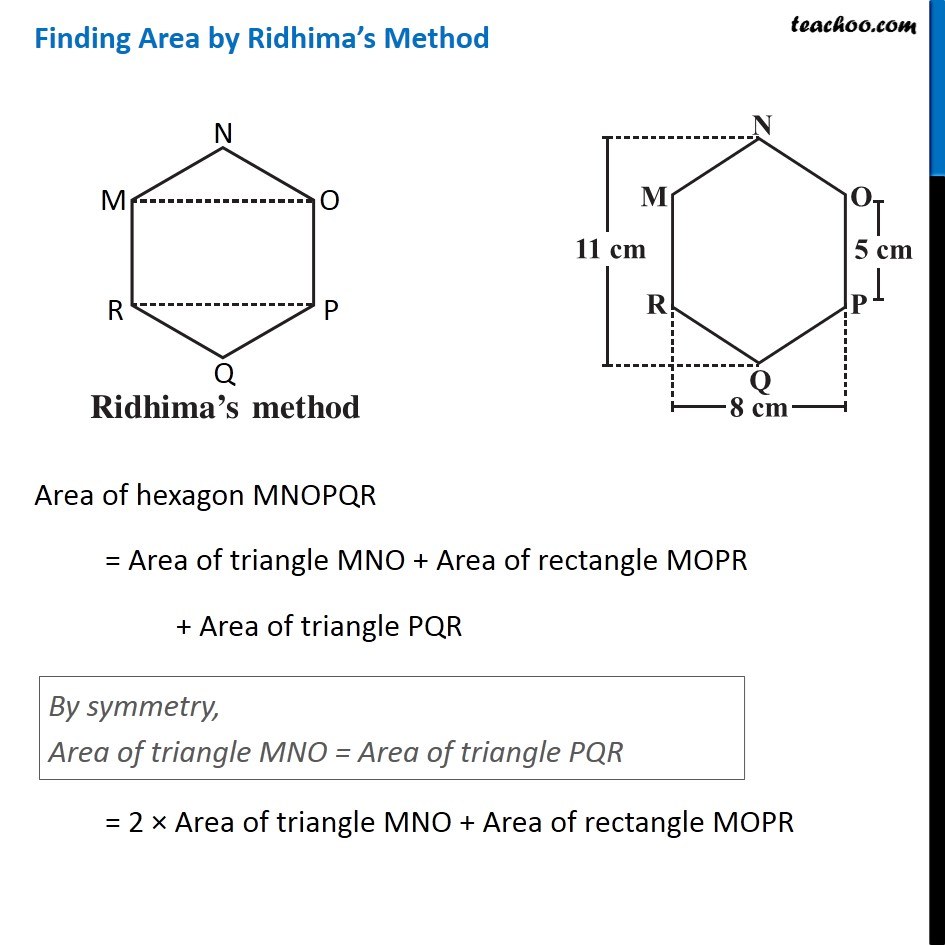
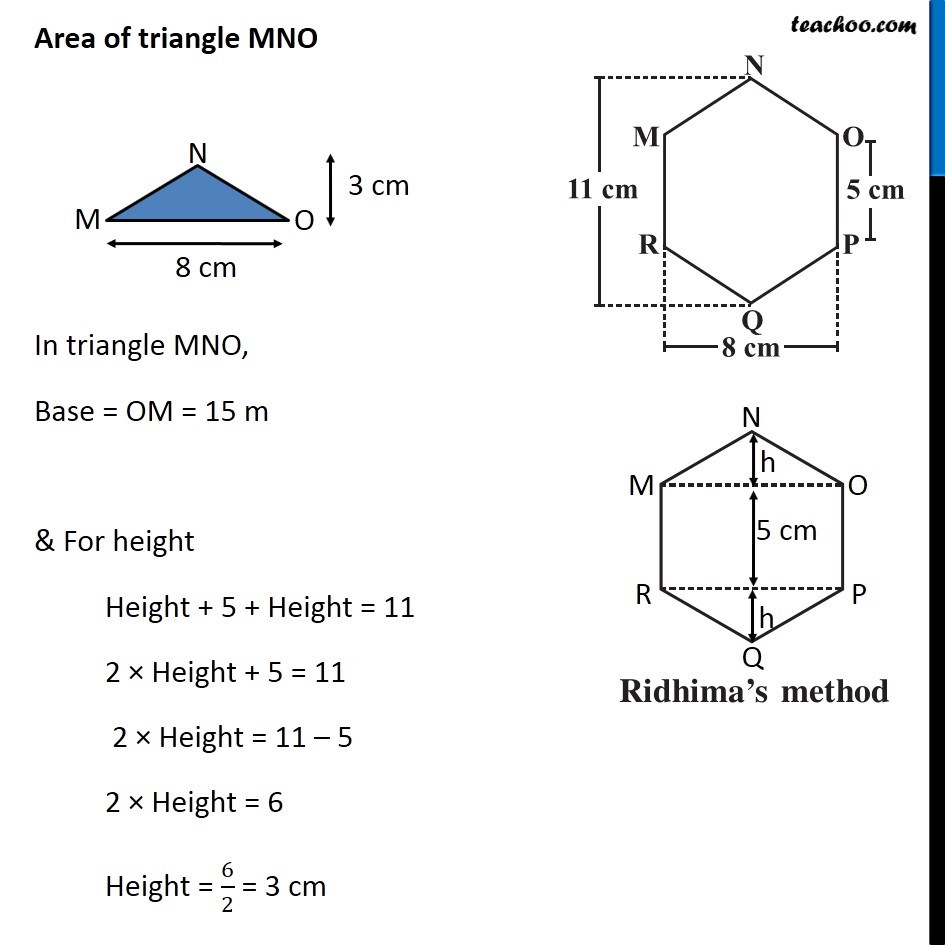
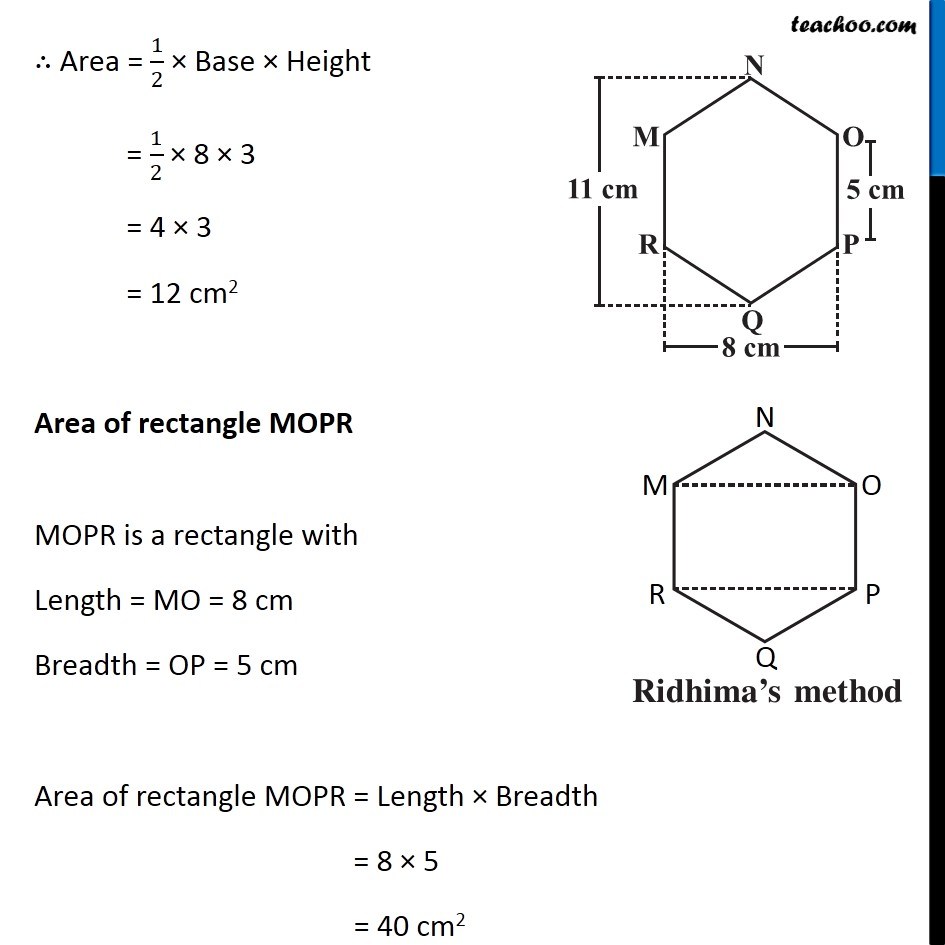
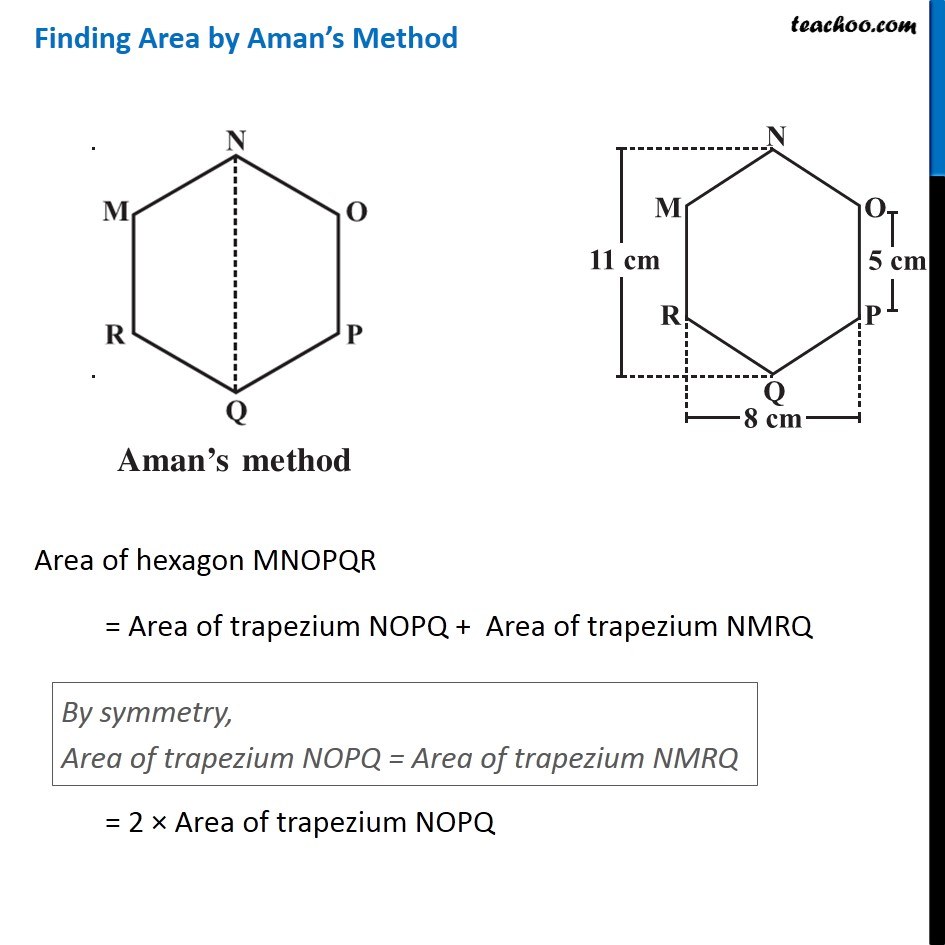
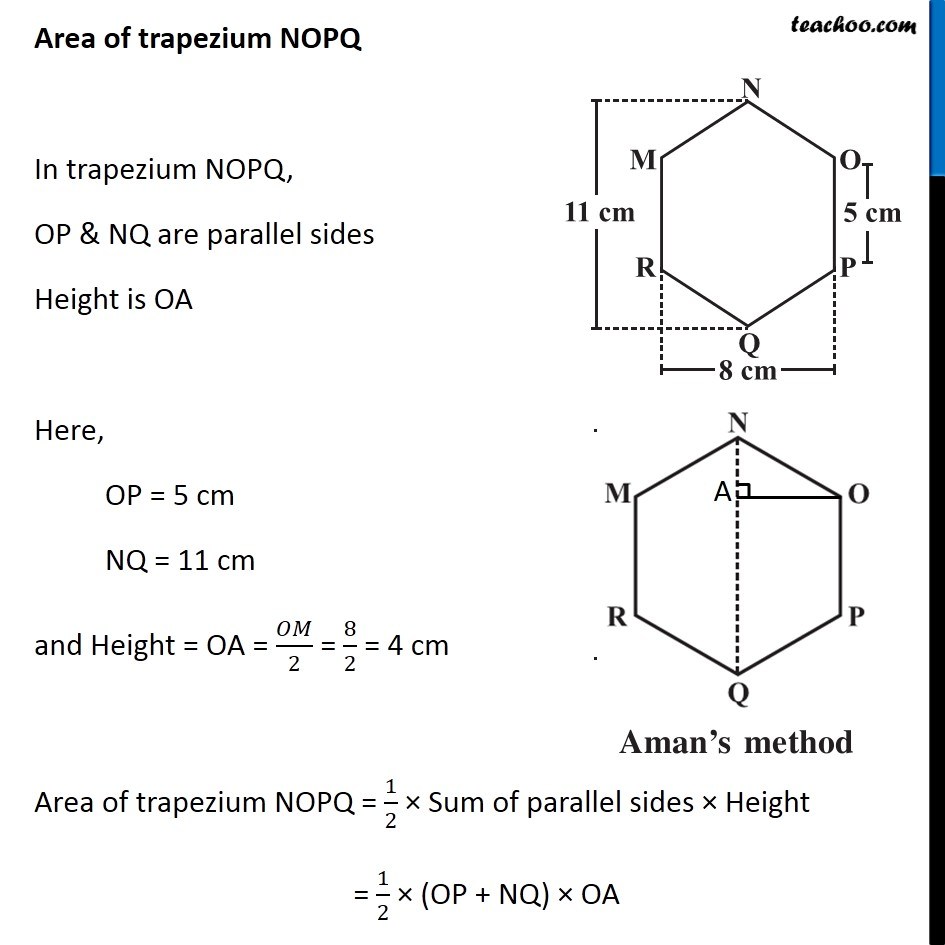
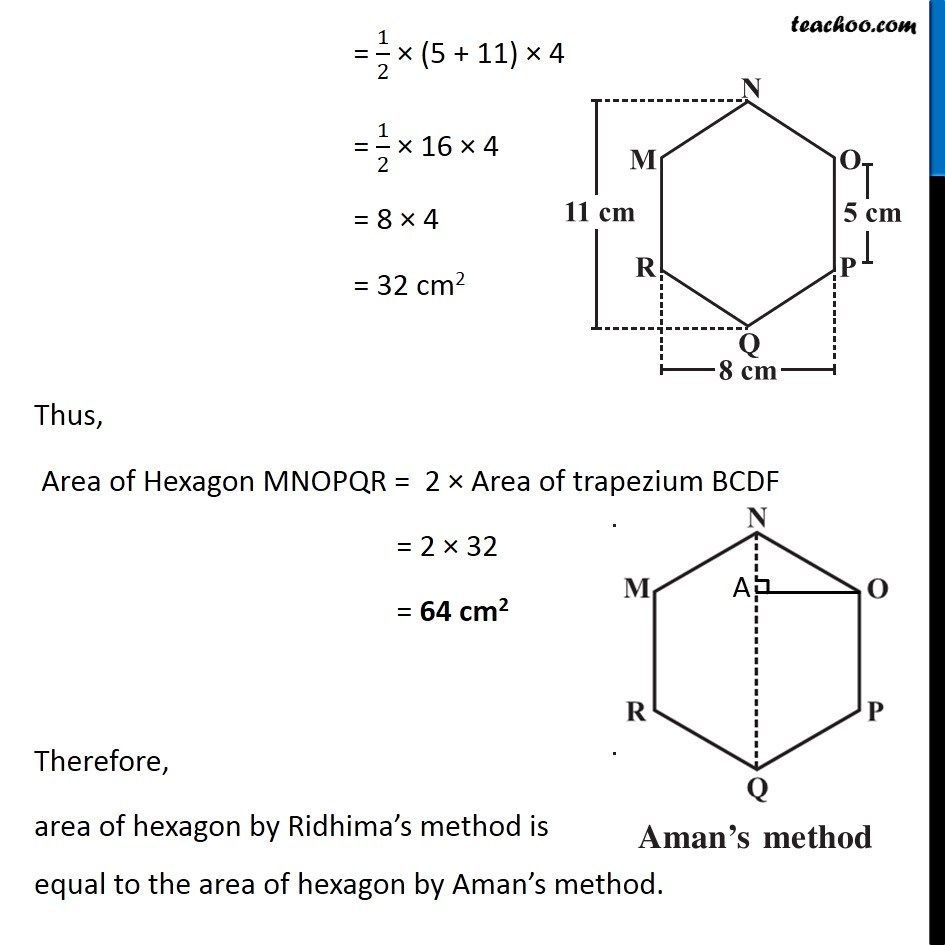
Example 3 There is a regular hexagon MNOPQR of side 5 cm (Fig 11.20) . Aman and Ridhima divided it in two different ways. Find the area of this hexagon using both ways (Fig 11.21). Finding Area by Ridhima’s Method Area of hexagon MNOPQR = Area of triangle MNO + Area of rectangle MOPR + Area of triangle PQR By symmetry, Area of triangle MNO = Area of triangle PQR = 2 × Area of triangle MNO + Area of rectangle MOPR Area of triangle MNO In triangle MNO, Base = OM = 15 m & For height Height + 5 + Height = 11 2 × Height + 5 = 11 2 × Height = 11 – 5 2 × Height = 6 Height = 6/2 = 3 cm ∴ Area = 1/2 × Base × Height = 1/2 × 8 × 3 = 4 × 3 = 12 cm2 Area of rectangle MOPR MOPR is a rectangle with Length = MO = 8 cm Breadth = OP = 5 cm Area of rectangle MOPR = Length × Breadth = 8 × 5 = 40 cm2 Thus, Area of hexagon MNOPQR = 2 × Area of triangle MNO + Area of rectangle MOPR = 2 × 12 + 40 = 24 + 40 = 64 cm2 Finding Area by Aman’s Method Area of hexagon MNOPQR = Area of trapezium NOPQ + Area of trapezium NMRQ By symmetry, Area of trapezium NOPQ = Area of trapezium NMRQ = 2 × Area of trapezium NOPQ Area of trapezium NOPQ In trapezium NOPQ, OP & NQ are parallel sides Height is OA Here, OP = 5 cm NQ = 11 cm and Height = OA = 𝑂𝑀/2 = 8/2 = 4 cm Area of trapezium NOPQ = 1/2 × Sum of parallel sides × Height = 1/2 × (OP + NQ) × OA = 1/2 × (5 + 11) × 4 = 1/2 × 16 × 4 = 8 × 4 = 32 cm2 Thus, Area of Hexagon MNOPQR = 2 × Area of trapezium BCDF = 2 × 32 = 64 cm2 Therefore, area of hexagon by Ridhima’s method is equal to the area of hexagon by Aman’s method.