
Finding Area of Polygons
Last updated at Dec. 16, 2024 by Teachoo





Transcript
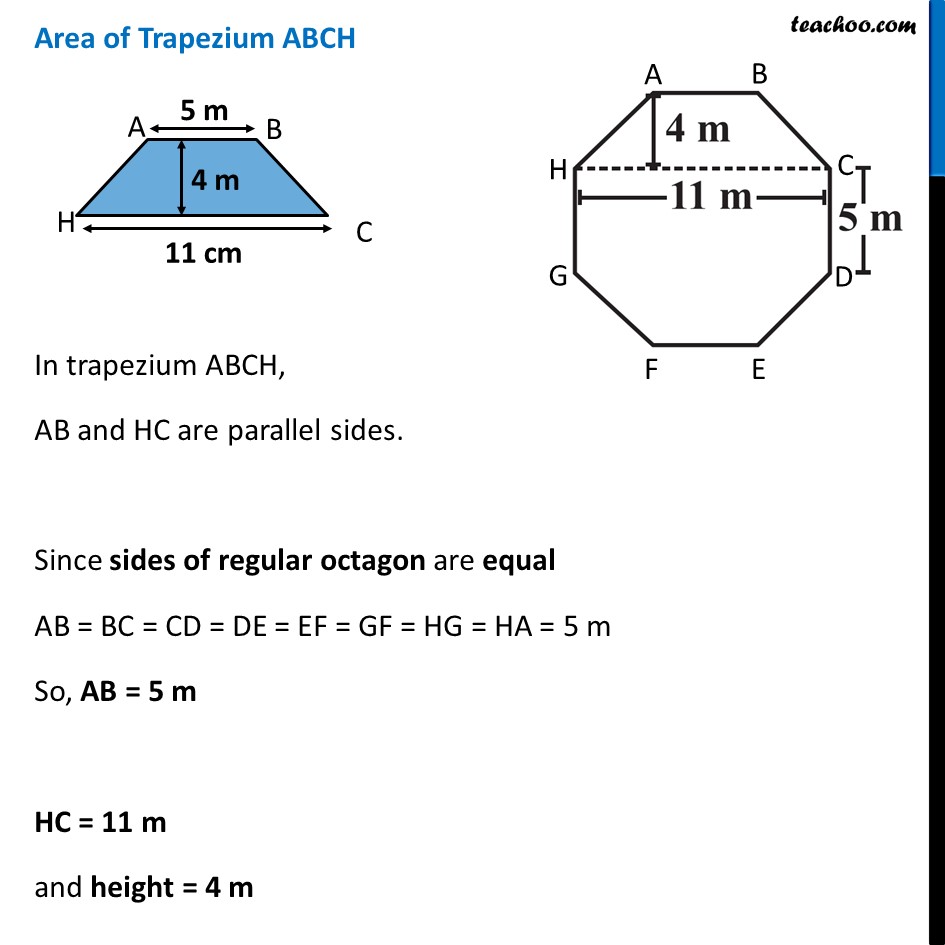
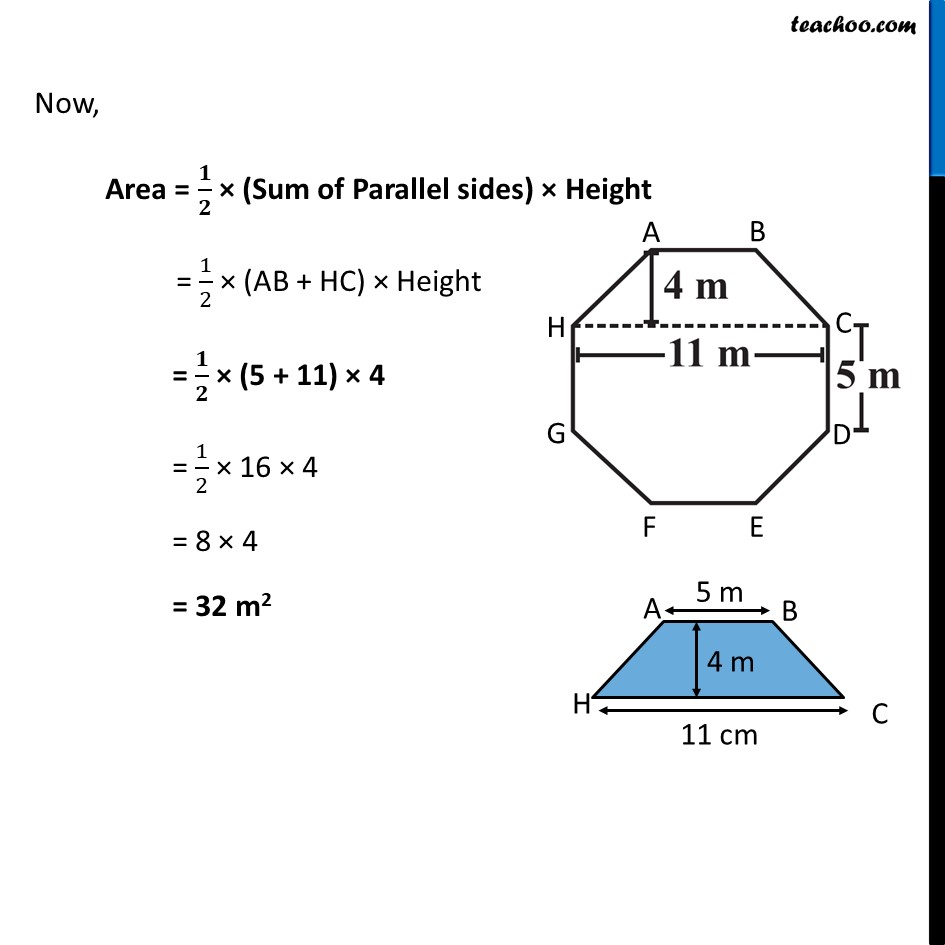
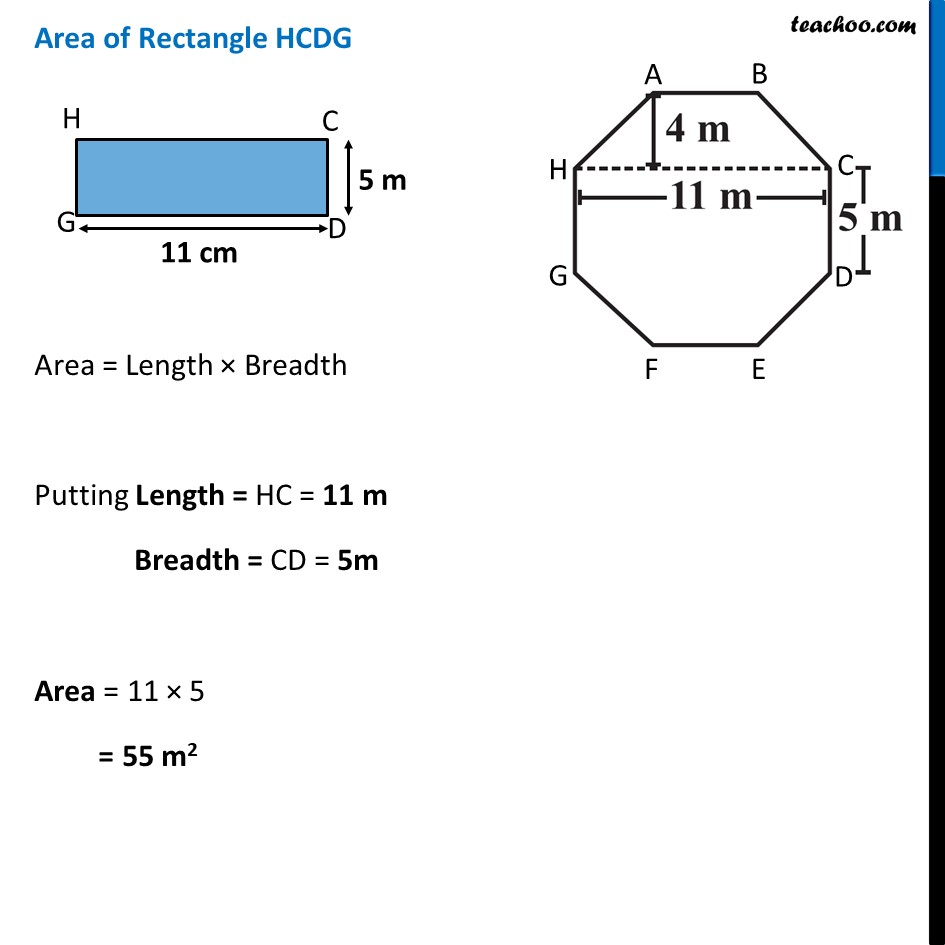
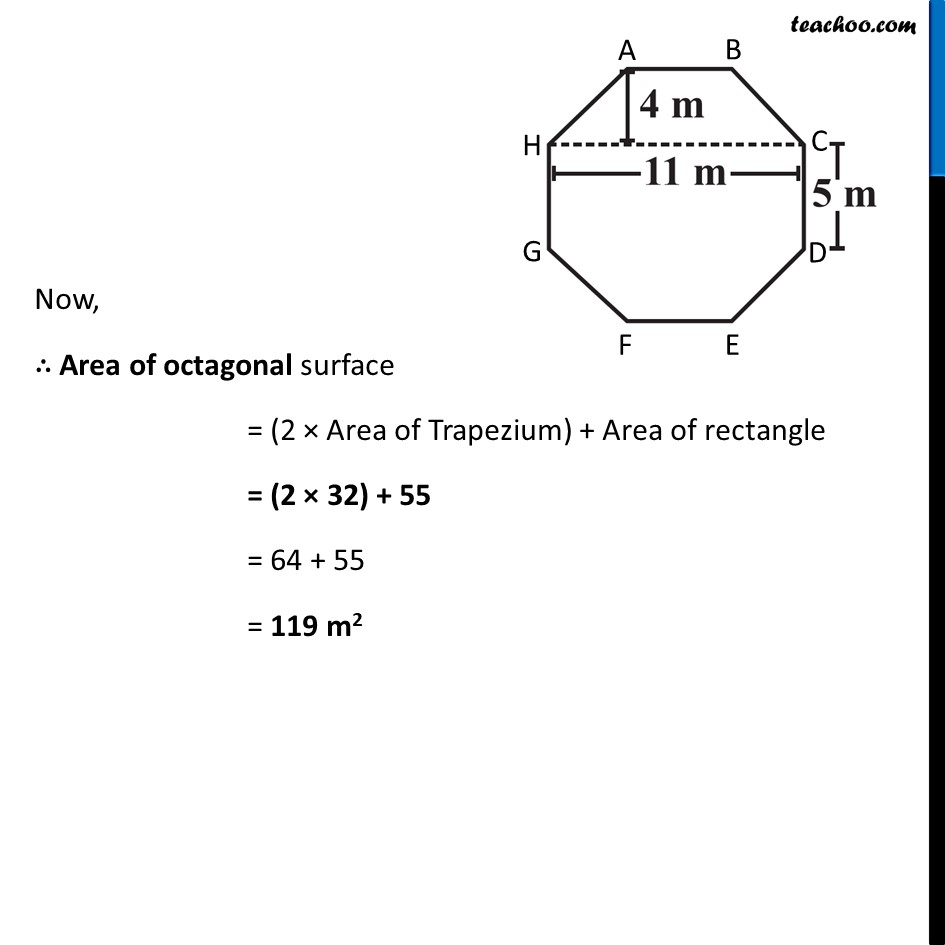
Ex 9.1, 9 Top surface of a raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.Area of octagonal surface = Area of trapezium ABCH + Area of rectangle HCDG + Area of Trapezium GDEF ∴ Area = (2 × Area of trapezium ABCH) + Area of rectangle HCDG Area of Trapezium ABCH In trapezium ABCH, AB and HC are parallel sides. Since sides of regular octagon are equal AB = BC = CD = DE = EF = GF = HG = HA = 5 m So, AB = 5 m HC = 11 m and height = 4 m Now, Area = 1/2 × (Sum of Parallel sides) × Height = 1/2 × (AB + HC) × Height Now, Area = 𝟏/𝟐 × (Sum of Parallel sides) × Height = 1/2 × (AB + HC) × Height = 𝟏/𝟐 × (5 + 11) × 4 = 1/2 × 16 × 4 = 8 × 4 = 32 m2 Area of Rectangle HCDG Area = Length × Breadth Putting Length = HC = 11 m Breadth = CD = 5m Area = 11 × 5 = 55 m2 Now, ∴ Area of octagonal surface = (2 × Area of Trapezium) + Area of rectangle = (2 × 32) + 55 = 64 + 55 = 119 m2