Question 10 (ii) - Area of Path and Cross roads - Worksheet - Chapter 9 Class 7 Perimeter and Area

Transcript

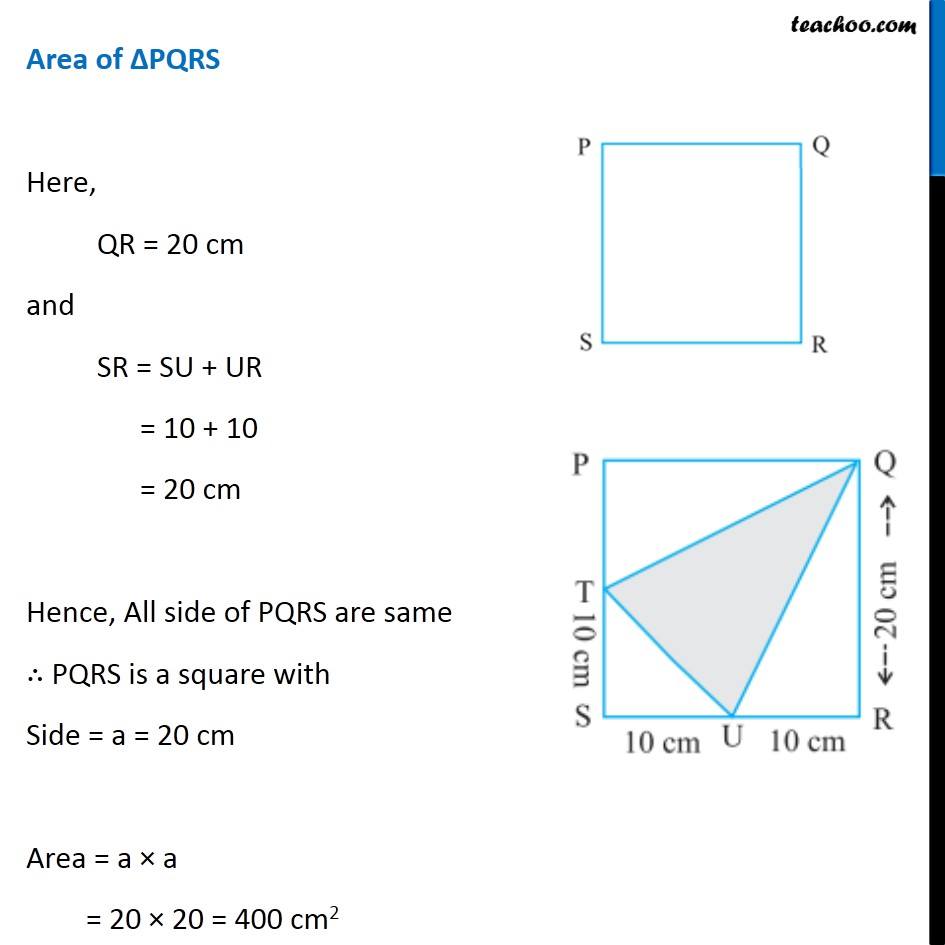
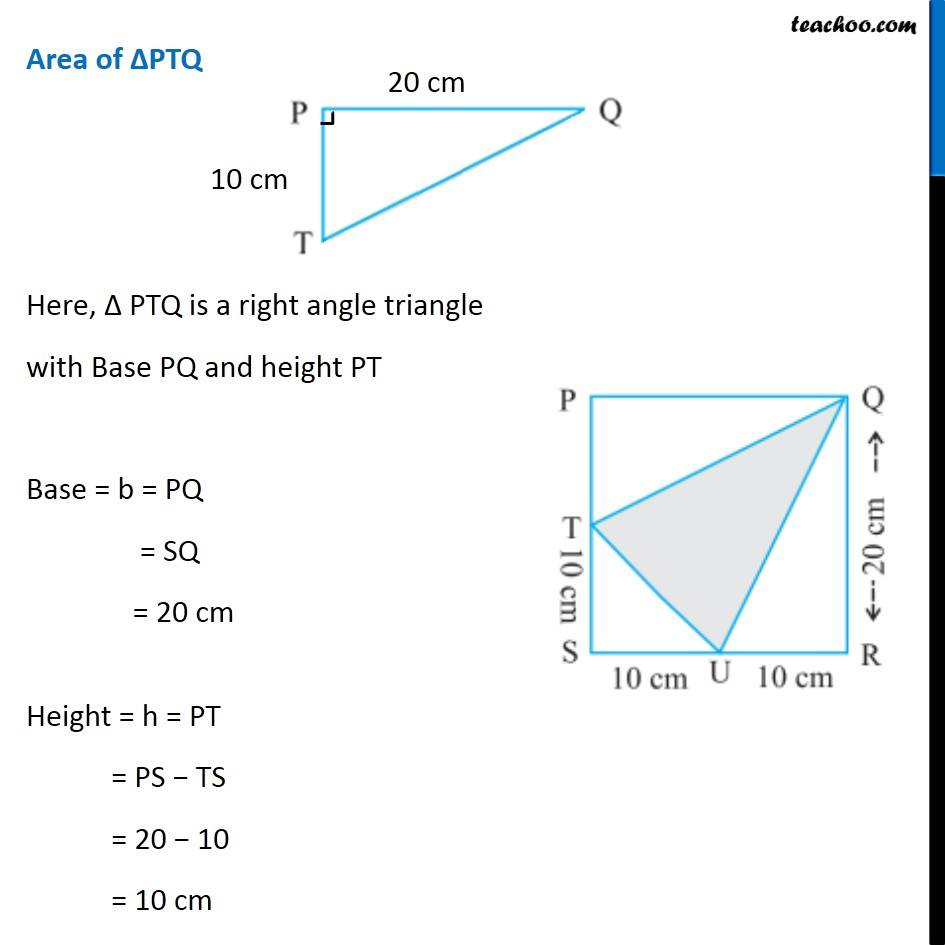
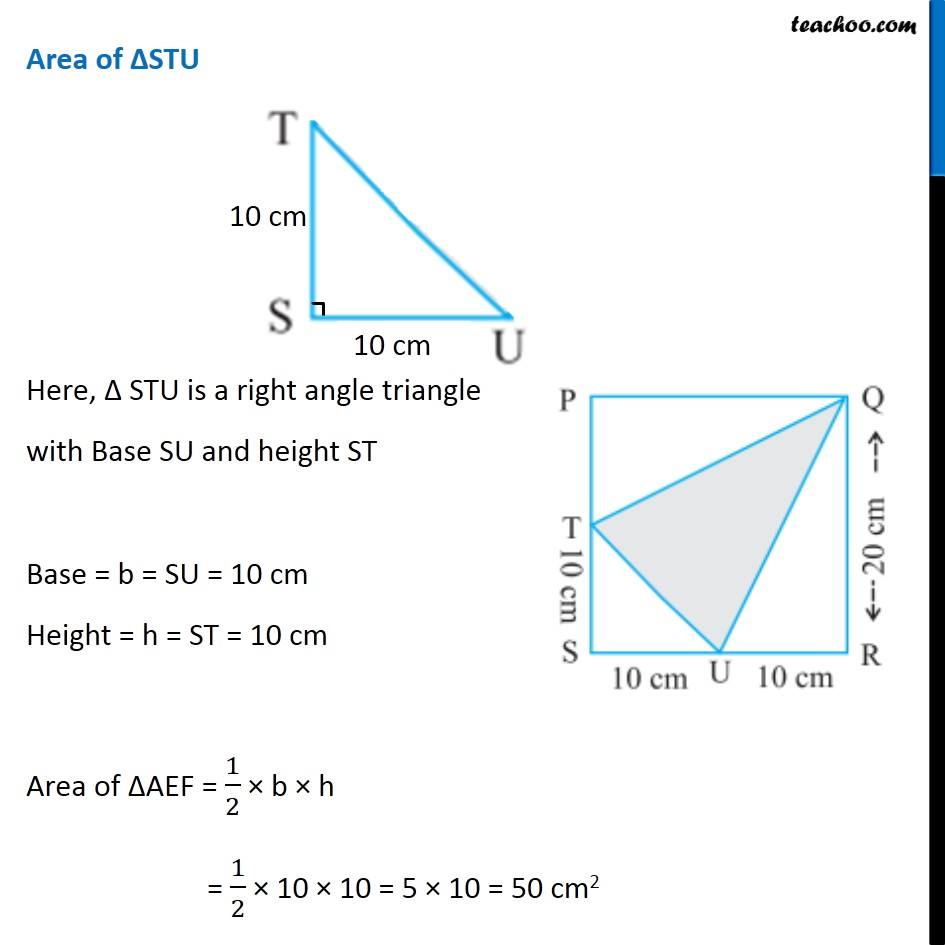
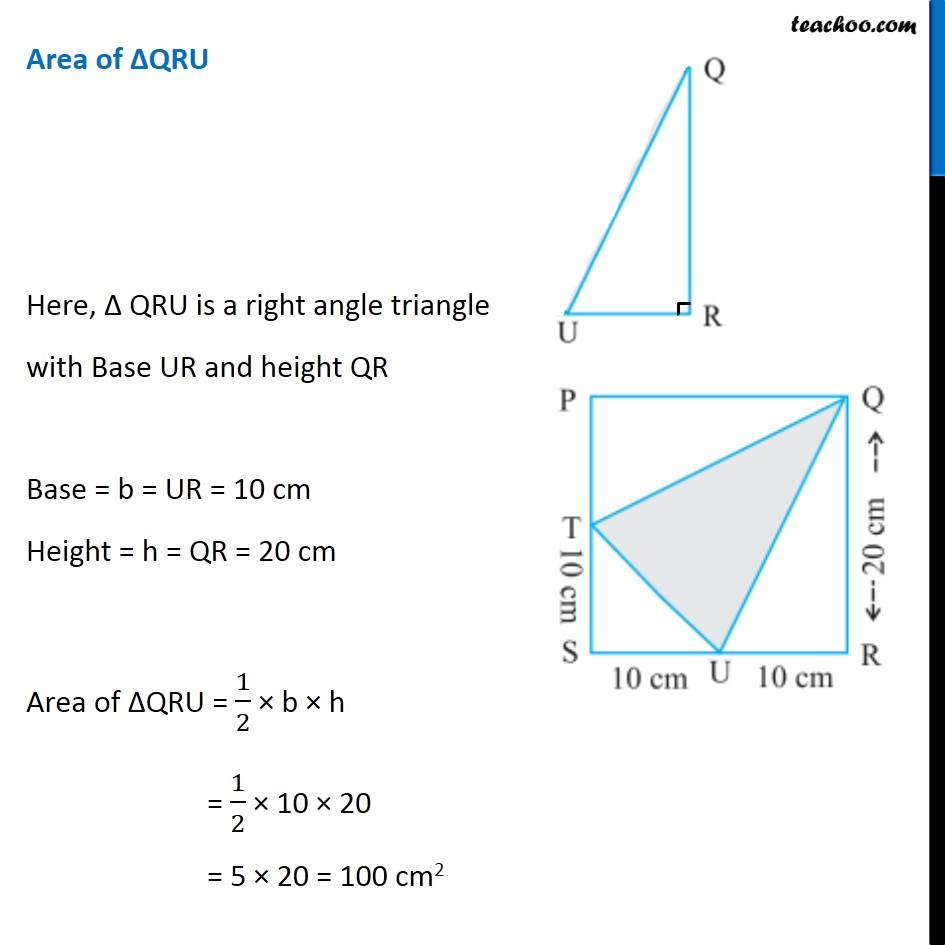
Question 10 (ii) In the following figures, find the area of the shaded portions: Area of shaded portion = Area of PQRS − Area of ∆PTQ − Area of ∆STU − Area of ∆QRU Area of ∆PQRS Here, QR = 20 cm and SR = SU + UR = 10 + 10 = 20 cm Hence, All side of PQRS are same ∴ PQRS is a square with Side = a = 20 cm Area = a × a = 20 × 20 = 400 cm2 Area of ∆PTQ Here, Δ PTQ is a right angle triangle with Base PQ and height PT Base = b = PQ = SQ = 20 cm Height = h = PT = PS − TS = 20 − 10 = 10 cm Area of ∆PTQ = 1/2 × b × h = 1/2 × 20 × 10 = 10 × 10 = 100 cm2 Area of ∆STU Here, Δ STU is a right angle triangle with Base SU and height ST Base = b = SU = 10 cm Height = h = ST = 10 cm Area of ∆AEF = 1/2 × b × h = 1/2 × 10 × 10 = 5 × 10 = 50 cm2 Area of ∆QRU Here, Δ QRU is a right angle triangle with Base UR and height QR Base = b = UR = 10 cm Height = h = QR = 20 cm Area of ∆QRU = 1/2 × b × h = 1/2 × 10 × 20 = 5 × 20 = 100 cm2 Now, Area of shaded portion = Area of PQRS − Area of ∆PTQ − Area of ∆STU − Area of ∆QRU = 400 − 100 − 50 − 100 = 400 − (100 + 50 + 100) = 400 − 250 = 150 cm2 ∴ Area of shaded portion is 150 cm2