Question 10 (i) - Area of Path and Cross roads - Worksheet - Chapter 9 Class 7 Perimeter and Area

Transcript

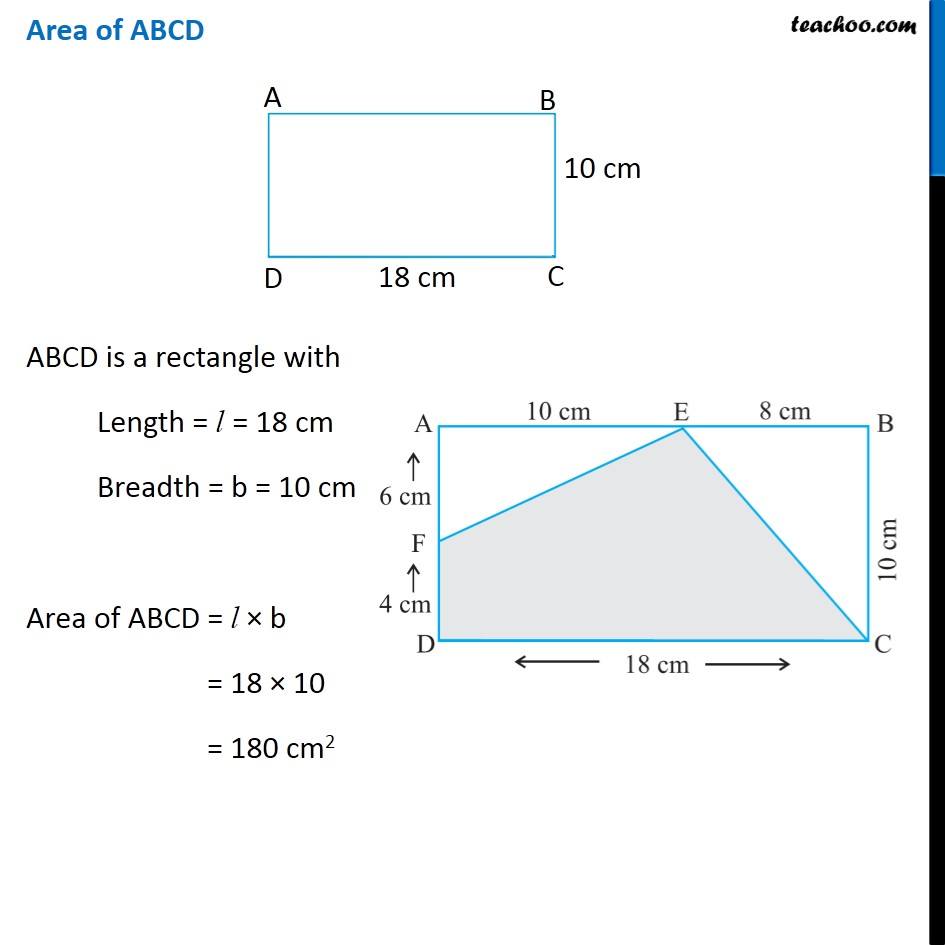
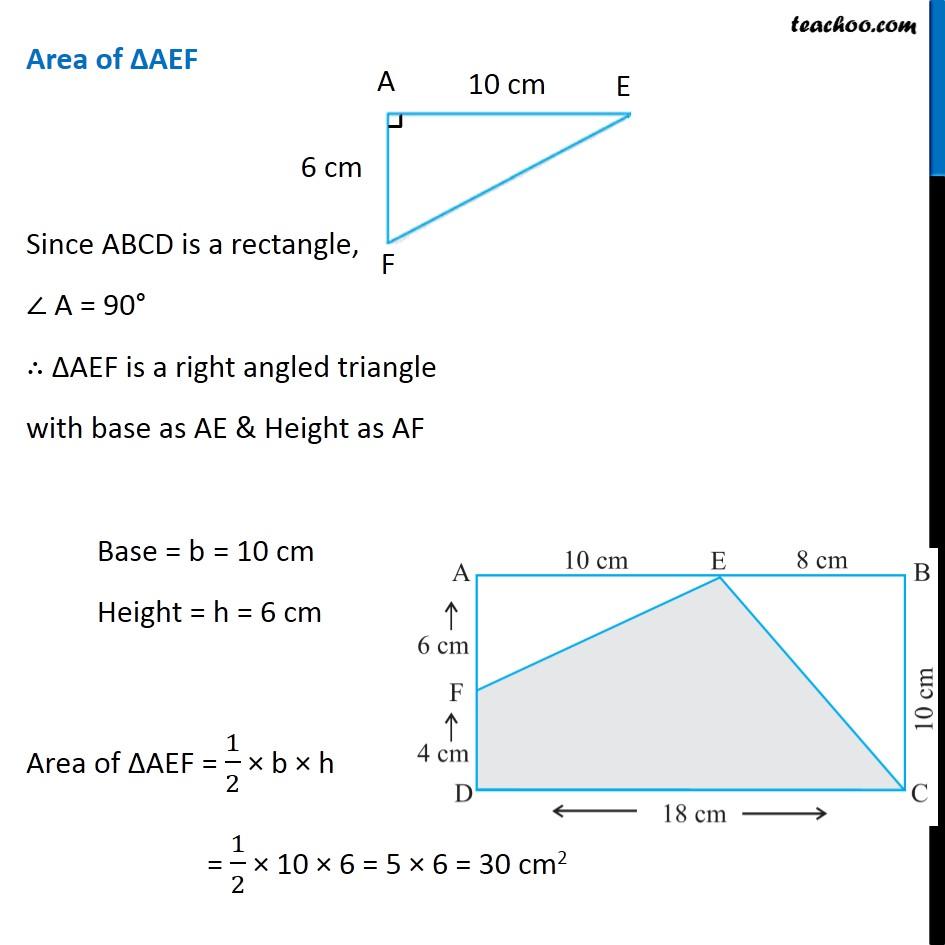
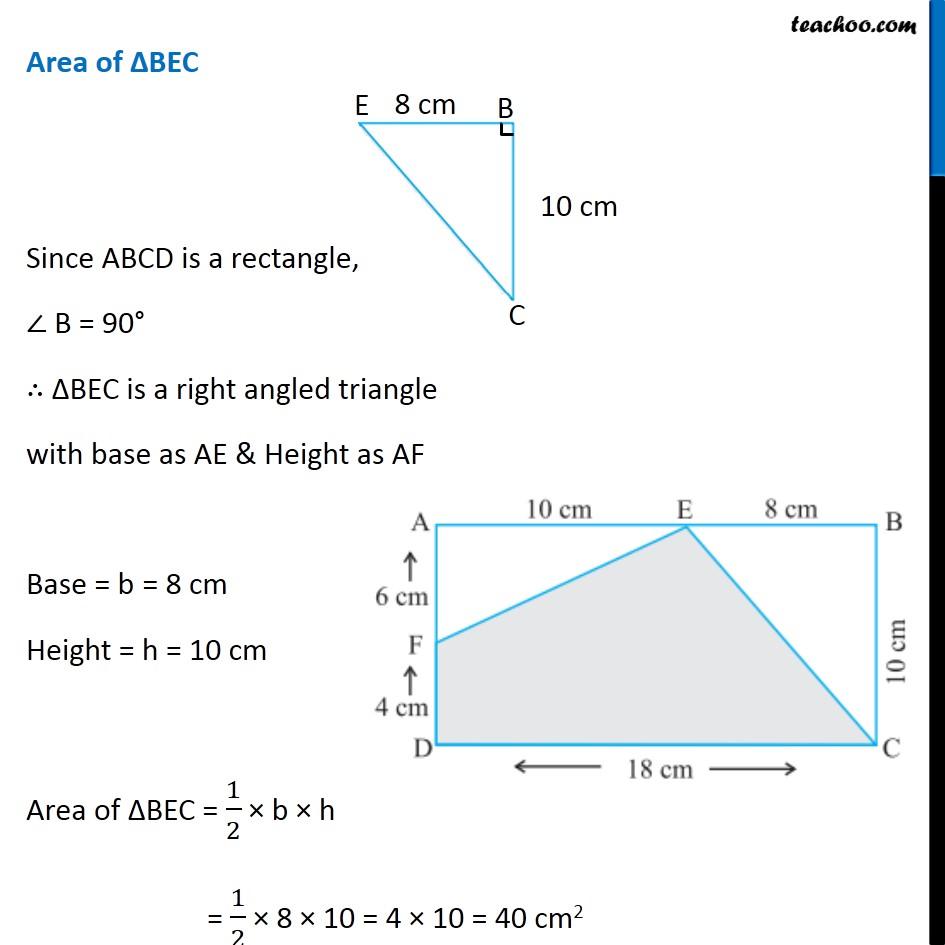
Question 10 (i) In the following figures, find the area of the shaded portions: Area of shaded portion = Area of ABCD − Area of ∆AEF − area of ∆BEC Area of ABCD ABCD is a rectangle with Length = l = 18 cm Breadth = b = 10 cm Area of ABCD = l × b = 18 × 10 = 180 cm2 Area of ∆AEF Since ABCD is a rectangle, ∠ A = 90° ∴ ∆AEF is a right angled triangle with base as AE & Height as AF Base = b = 10 cm Height = h = 6 cm Area of ∆AEF = 1/2 × b × h = 1/2 × 10 × 6 = 5 × 6 = 30 cm2 Area of ∆BEC Since ABCD is a rectangle, ∠ B = 90° ∴ ∆BEC is a right angled triangle with base as AE & Height as AF Base = b = 8 cm Height = h = 10 cm Area of ∆BEC = 1/2 × b × h = 1/2 × 8 × 10 = 4 × 10 = 40 cm2 Now, Area of shaded portion = Area of ABCD − Area of ∆AEF − Area of ∆BEC = 180 − 30 − 40 = 150 − 40 = 110 cm2 ∴ Area of shaded region is 110 cm2