Question 4 - Area of Path and Cross roads - Worksheet - Chapter 9 Class 7 Perimeter and Area

Transcript

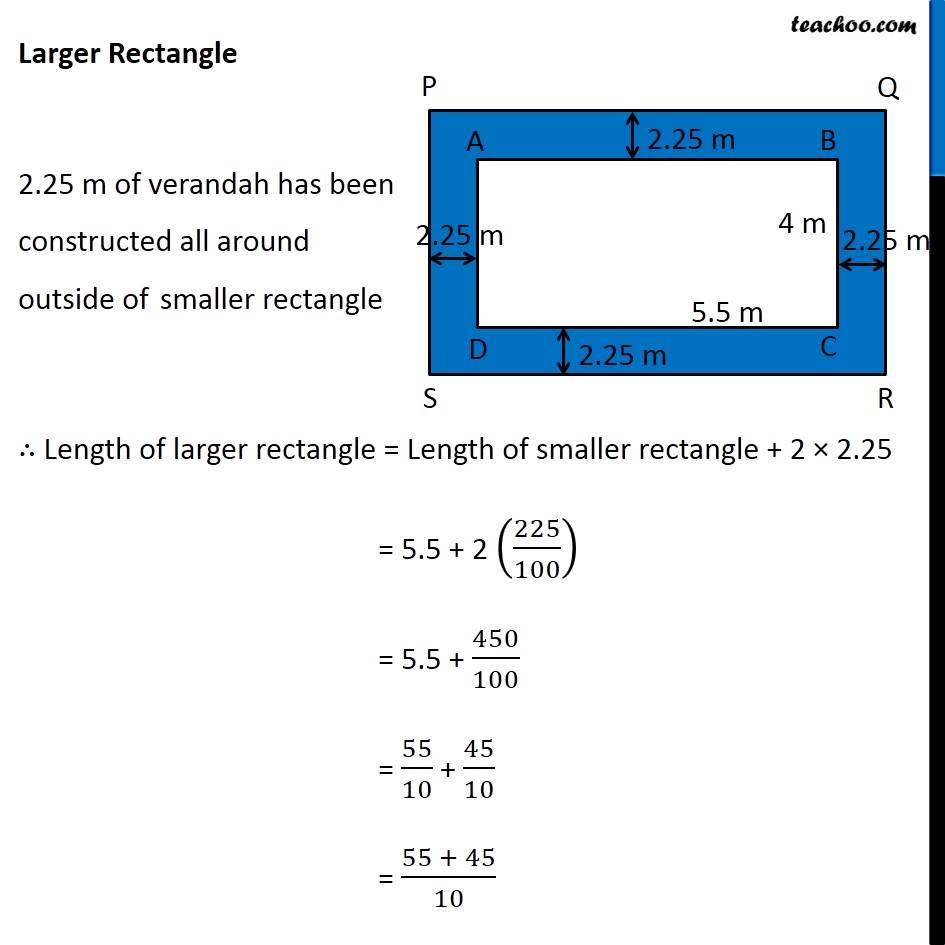
Question 4 A verandah of width 2.25 m is constructed all along outside a room which is 5.5 m long and 4 m wide. Find: (i) the area of the verandah. Here, Area of verandah = Area of larger rectangle − Area of smaller rectangle Finding length and breadth of both rectangles Smaller rectangle Length of smaller rectangle = 5.5 m Breadth of smaller rectangle = 4 m Larger Rectangle 2.25 m of verandah has been constructed all around outside of smaller rectangle ∴ Length of larger rectangle = Length of smaller rectangle + 2 × 2.25 = 5.5 + 2 (225/100) = 5.5 + 450/100 = 55/10 + 45/10 = (55 + 45)/10 = 100/10 = 10 m ∴ Breadth of larger rectangle = Breadth of smaller rectangle + 2 × 2.25 = 4 + 2 (225/100) = 4 + 450/100 = 4 + 45/10 = (4 × 10 + 45)/10 = (40 + 45)/10 = 85/10 = 8.5 m Larger rectangle Length = l = 10 m Breadth = b = 8.5 m Area of larger rectangle = l × b = 10 × 8.5 = 10 × 85/10 = 85 m2 Smaller rectangle Length = l = 5.5 m Breadth = b = 4 m Area of smaller rectangle = l × b = 5.5 × 4 = 55/10 × 4 = 55/5 × 2 = 11 × 2 Now, Area of verandah = Area of larger rectangle − Area of smaller rectangle = 85 − 22 = 63 m2 ∴ Area of path is 63 m2 Question 4 A verandah of width 2.25 m is constructed all along outside a room which is 5.5 m long and 4 m wide. Find: (ii) the cost of cementing the floor of the verandah at the rate of Rs 200 per m2. Cost of cementing verandah in 1 m2 = Rs 200 Cost of cementing verandah in 63 m2 = Rs 200 × 63 = Rs 12,600 ∴ It will cost Rs 12,600 for it’s cementing Cost of cementing verandah in 1 m2 = Rs 200 Cost of cementing verandah in 63 m2 = Rs 200 × 63 = Rs 12,600 ∴ It will cost Rs 12,600 for it’s cementing Cost of cementing verandah in 1 m2 = Rs 200 Cost of cementing verandah in 63 m2 = Rs 200 × 63 = Rs 12,600 ∴ It will cost Rs 12,600 for it’s cementing Cost of cementing verandah in 1 m2 = Rs 200 Cost of cementing verandah in 63 m2 = Rs 200 × 63 = Rs 12,600 ∴ It will cost Rs 12,600 for it’s cementing Cost of cementing verandah in 1 m2 = Rs 200 Cost of cementing verandah in 63 m2 = Rs 200 × 63 = Rs 12,600 ∴ It will cost Rs 12,600 for it’s cementing Cost of cementing verandah in 1 m2 = Rs 200 Cost of cementing verandah in 63 m2 = Rs 200 × 63 = Rs 12,600 ∴ It will cost Rs 12,600 for it’s cementing