Question 4 - Important Coordinate Geometry Questions - Chapter 7 Class 10 Coordinate Geometry

Transcript

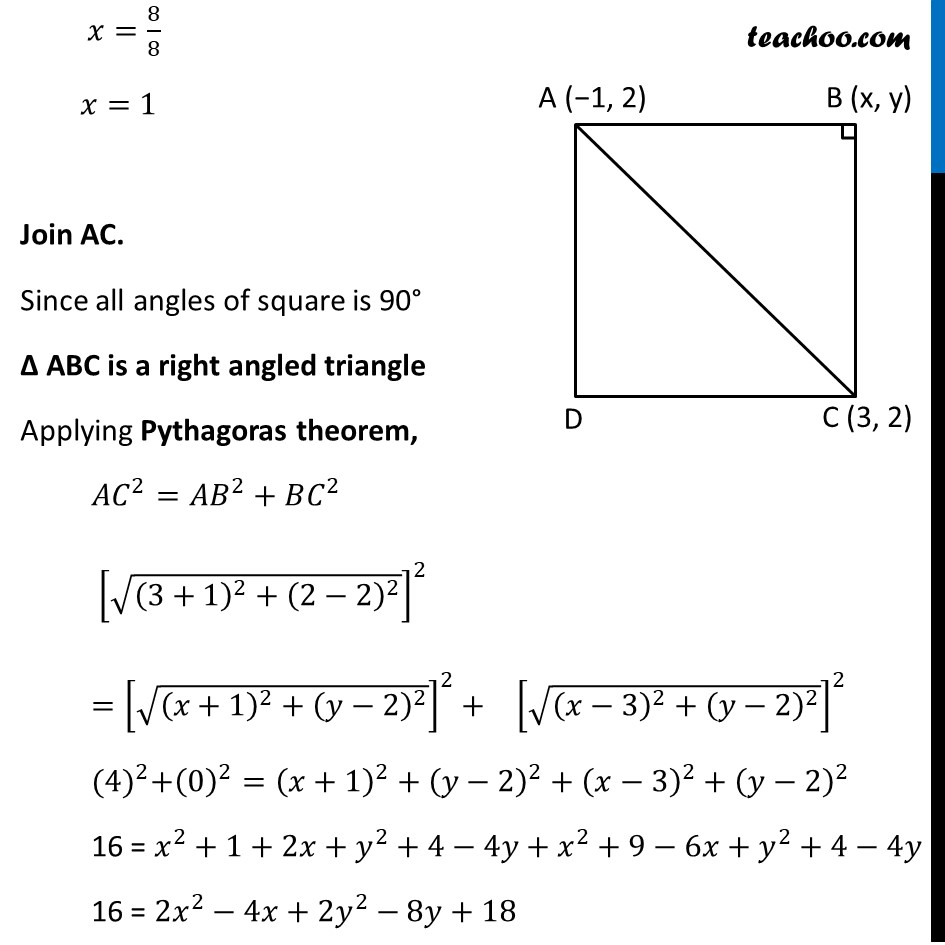
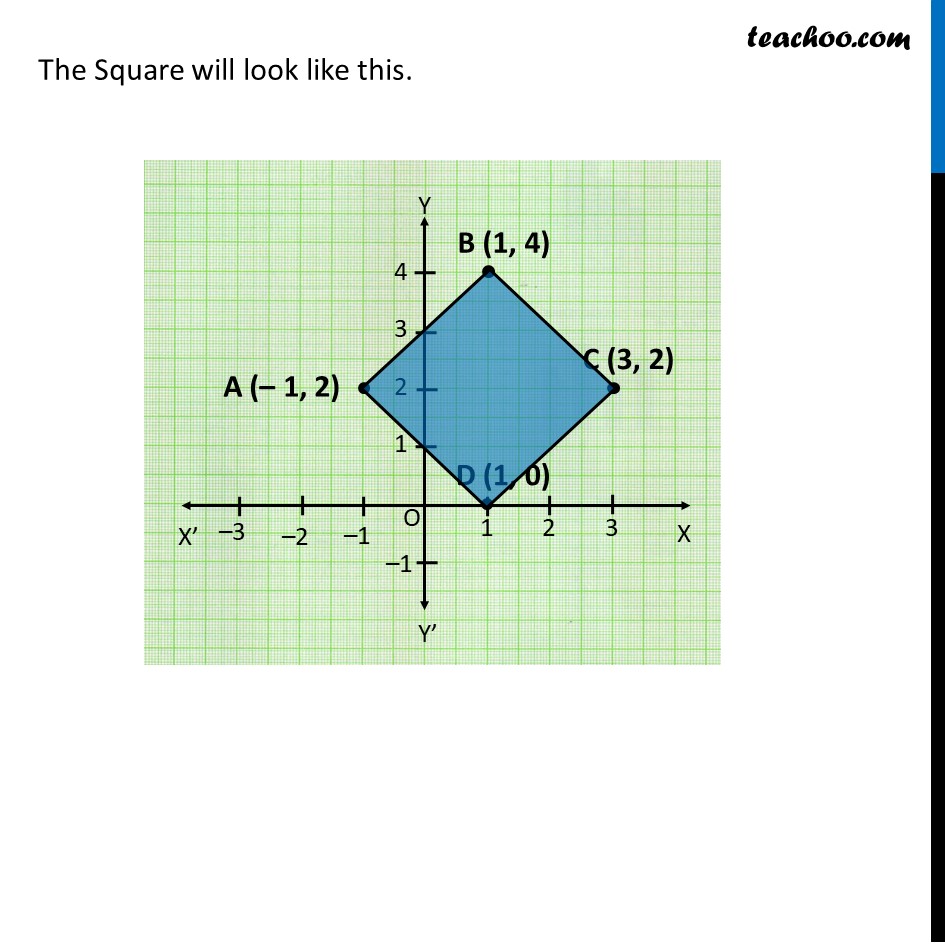
Question 4 The two opposite vertices of a square are (–1, 2) and (3, 2). Find the coordinates of the other two vertices. The two given vertices of the square ABCD are A(−1, 2) and C(3, 2). Let B(x, y) be the unknown vertex. We know, all the sides of square are equal. AB = CB Using Distance Formula, AB = √((𝑥+1)^2+(𝑦−2)^2 ) CB = √((𝑥−3)^2+(𝑦−2)^2 ) Now, AB = CB √((𝑥+1)^2+(𝑦−2)^2 )=√((𝑥−3)^2+(𝑦−2)^2 ) Cancelling the square roots (𝑥+1)^2+(𝑦−2)^2= (𝑥−3)^2+(𝑦−2)^2 (𝑥+1)^2= (𝑥−3)^2+(𝒚−𝟐)^𝟐−(𝒚−𝟐)^𝟐 (𝑥+1)^2=(𝑥−3)^2 (𝑥+1)^2−(𝑥−3)^2=0 𝑥^2+1+2𝑥−(𝑥^2+9−6𝑥)=0 𝑥^2+1+2𝑥−𝑥^2−9+6𝑥=0 8𝑥−8=0 8𝑥=8 𝑥=8/8 𝑥=1 Join AC. Since all angles of square is 90° Δ ABC is a right angled triangle Applying Pythagoras theorem, 〖𝐴𝐶〗^2=𝐴𝐵^2+𝐵𝐶^2 [√((3+1)^2+(2−2)^2 )]^2 =[√((𝑥+1)^2+(𝑦−2)^2 )]^2+ [√((𝑥−3)^2+(𝑦−2)^2 )]^2 〖(4)〗^2+(0)^2=(𝑥+1)^2+(𝑦−2)^2+(𝑥−3)^2+(𝑦−2)^2 16 = 𝑥^2+1+2𝑥+𝑦^2+4−4𝑦+𝑥^2+9−6𝑥+𝑦^2+4−4𝑦 16 = 〖2𝑥〗^2−4𝑥+2𝑦^2−8𝑦+18 Putting x = 1 16 = 〖2(1)〗^2−4(1)+2𝑦^2−8𝑦+18 16 = 2 − 4 + 〖2𝑦〗^2−8𝑦+18 16 = 16 + 〖2𝑦〗^2−8𝑦 16 − 16 = 〖2𝑦〗^2−8𝑦 0 = 〖2𝑦〗^2−8𝑦 0 = 2𝑦 (𝑦−4) 𝑦 (𝑦−4) = 0 So, 𝑦=0 and 𝑦 −4=0 So, 𝑦=0 and 𝑦=4 Thus, the other two vertices are (1, 0) and (1, 4). The Square will look like this.