You are here
Ex 8.2 , 7 (MCQ) - Chapter 8 Class 12 Application of Integrals
Last updated at Dec. 16, 2024 by Teachoo
Chapter 8 Class 12 Application of Integrals
Serial order wise
- Ex 8.1
- Examples
- Miscellaneous
- Case Based Questions (MCQ)
-
Area between 2 curves
Transcript
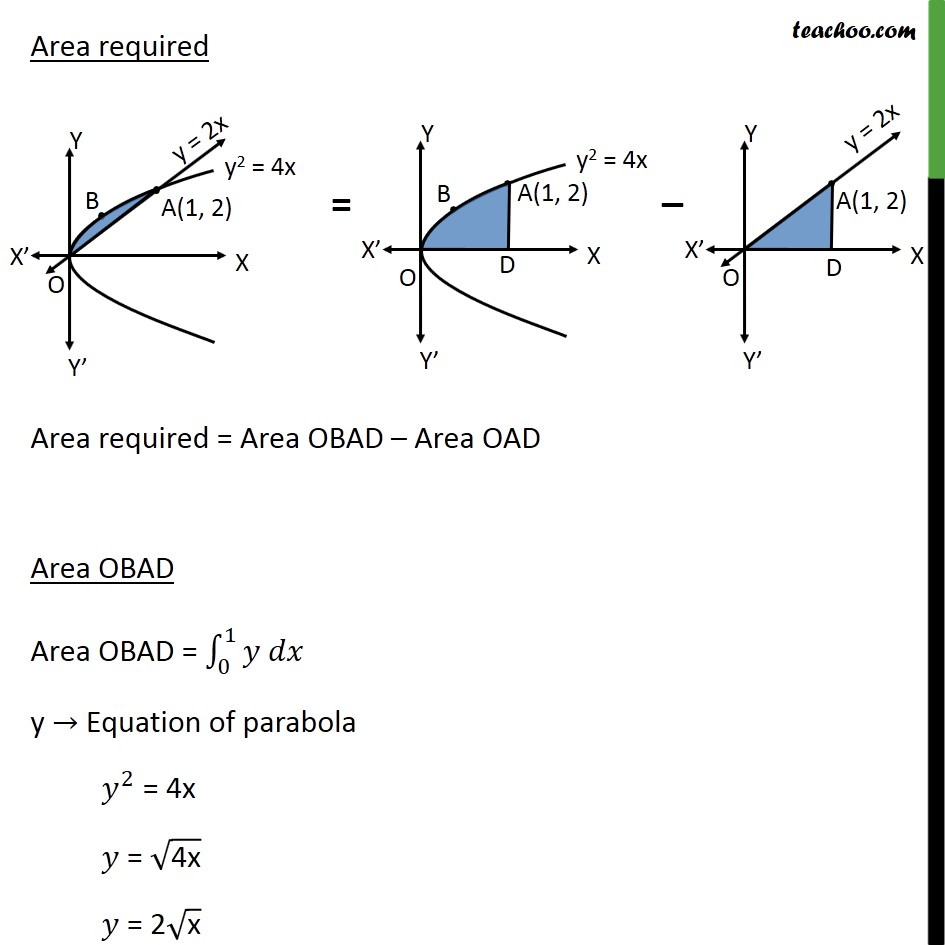
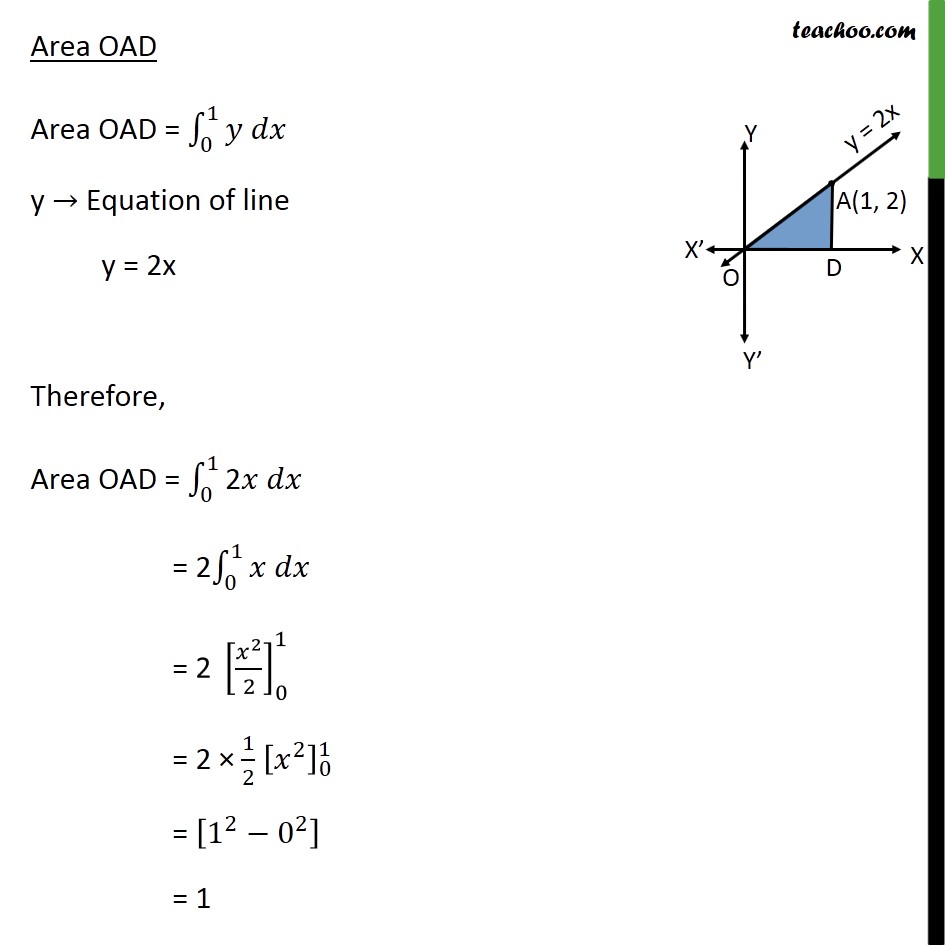
Ex 8.2 , 7 Area lying between the curves 2 = 4 and =2 is (A) (B) (C) (D) Step 1: Drawing figure Parabola is 2 =4x Also, =2 passes through (0, 0) & (1, 2) Point (1, 2) lies in parabola y2 = 4x Hence, intersecting point A = (1, 2) Area required Area required = Area OBAD Area OAD Area OBAD Area OBAD = 0 1 y Equation of parabola 2 = 4x = 4x = 2 x Therefore, Area OBAD = 0 1 2 x = 2 0 1 1 2 = 2 1 2 +1 1 2 +1 0 1 = 2 3 2 3 2 0 1 = 2 2 3 3 2 0 1 = 4 3 1 3 2 0 3 2 = 4 3 Area OAD Area OAD = 0 1 y Equation of line y = 2x Therefore, Area OAD = 0 1 2 = 2 0 1 = 2 2 2 0 1 = 2 1 2 2 0 1 = 1 2 0 2 = 1 Area required = Area OBAD Area OAD = 4 3 1 = 1 3 So, B is correct option
