![[Class 7] Through construction, explore if it is possible to construct - Figure it out - Page 170, 171](https://cdn.teachoo.com/b18230a9-49ea-413c-bc83-cabe0ee7773e/slide89.jpg)
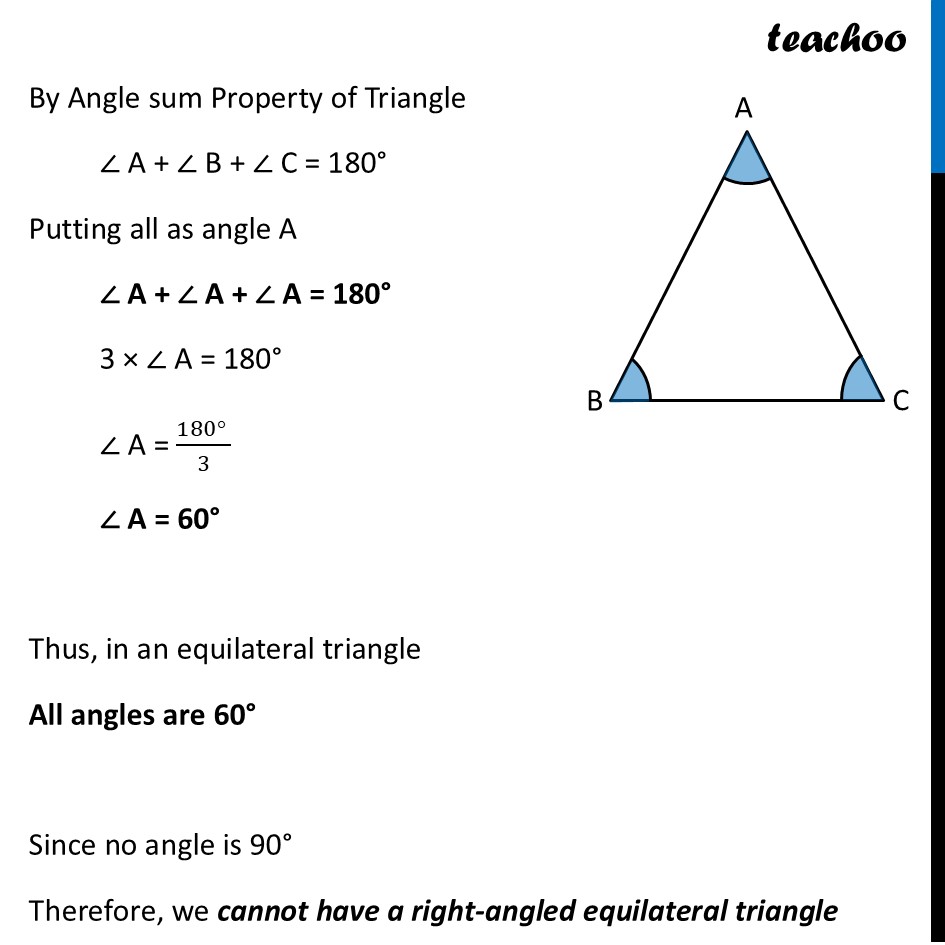
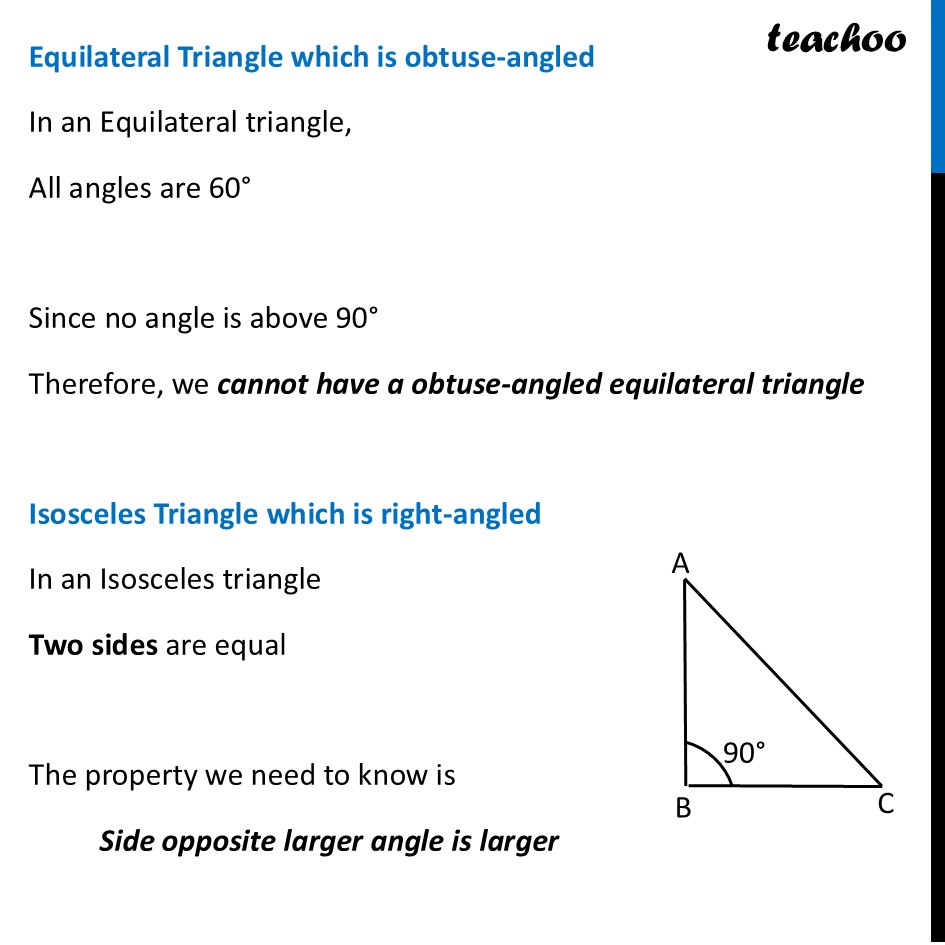
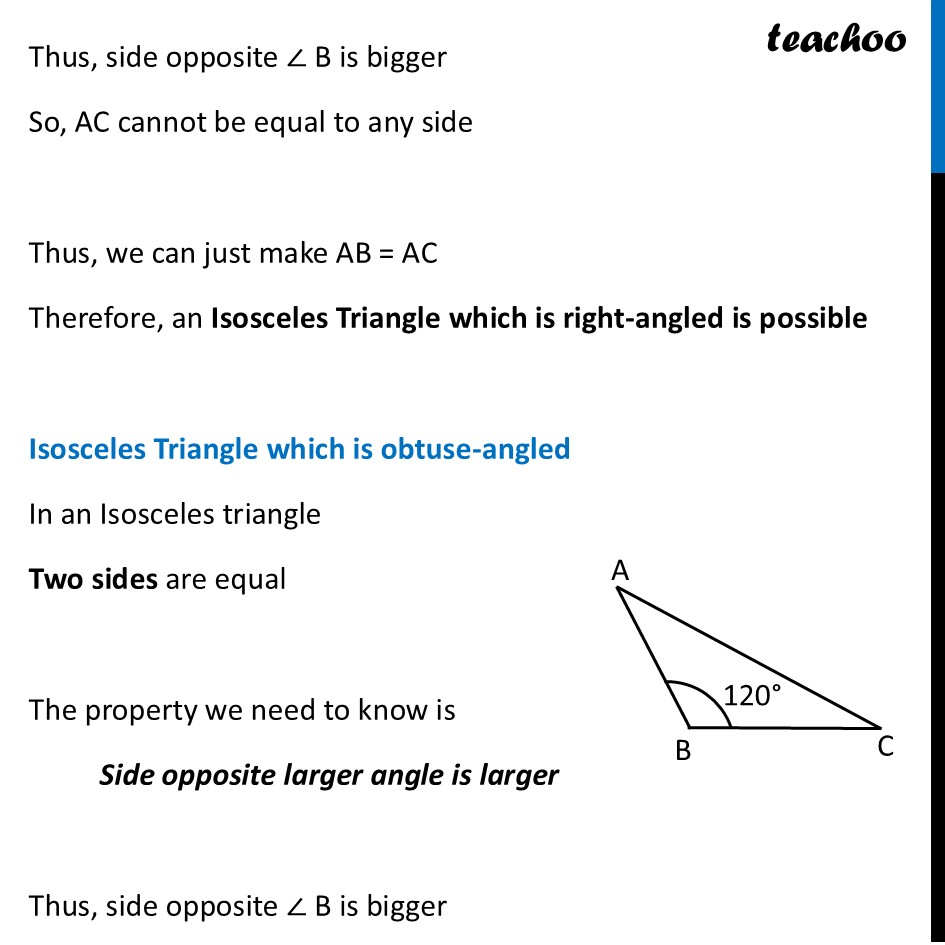

Figure it out - Page 170, 171
Last updated at November 7, 2025 by Teachoo
![[Class 7] Through construction, explore if it is possible to construct - Figure it out - Page 170, 171](https://cdn.teachoo.com/b18230a9-49ea-413c-bc83-cabe0ee7773e/slide89.jpg)




Transcript
Question 4 Through construction, explore if it is possible to construct an equilateral triangle that is (i) right-angled (ii) obtuse-angled. Also construct an isosceles triangle that is (i) right-angled (ii) obtuse-angled. Let’s do one by one Equilateral Triangle which is right-angled In an Equilateral triangle All sides are equal All angles are equal Here ∠ A = ∠ B = ∠ C By Angle sum Property of Triangle ∠ A + ∠ B + ∠ C = 180° Putting all as angle A ∠ A + ∠ A + ∠ A = 180° 3 × ∠ A = 180° ∠ A = (180° )/3 ∠ A = 60° Thus, in an equilateral triangle All angles are 60° Since no angle is 90° Therefore, we cannot have a right-angled equilateral triangle Equilateral Triangle which is obtuse-angled In an Equilateral triangle, All angles are 60° Since no angle is above 90° Therefore, we cannot have a obtuse-angled equilateral triangle Isosceles Triangle which is right-angled In an Isosceles triangle Two sides are equal The property we need to know is Side opposite larger angle is larger Thus, side opposite ∠ B is bigger So, AC cannot be equal to any side Thus, we can just make AB = AC Therefore, an Isosceles Triangle which is right-angled is possible Isosceles Triangle which is obtuse-angled In an Isosceles triangle Two sides are equal The property we need to know is Side opposite larger angle is larger Thus, side opposite ∠ B is bigger So, AC cannot be equal to any side Thus, we can just make AB = AC Therefore, an Isosceles Triangle which is obtuse-angled is possible