Question 3 - Figure it out - Page 170, 171 - Chapter 7 Class 7 - A tale of three Intersecting Lines (Ganit Prakash)

Transcript

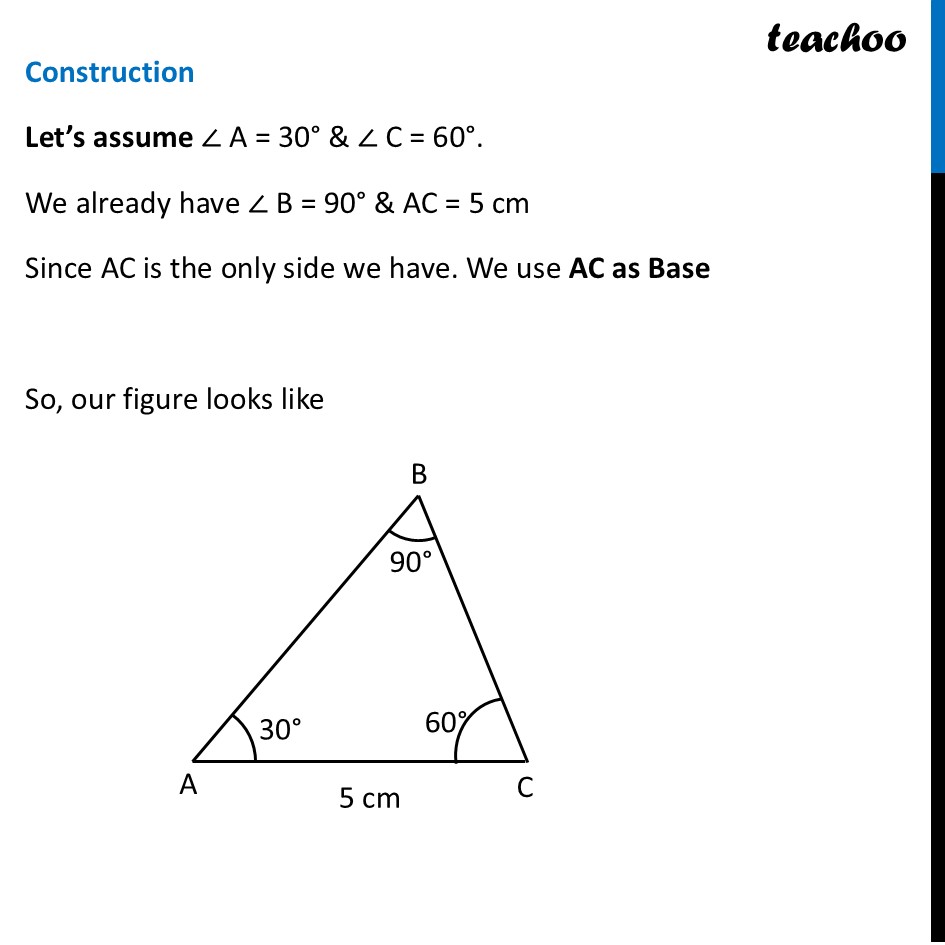
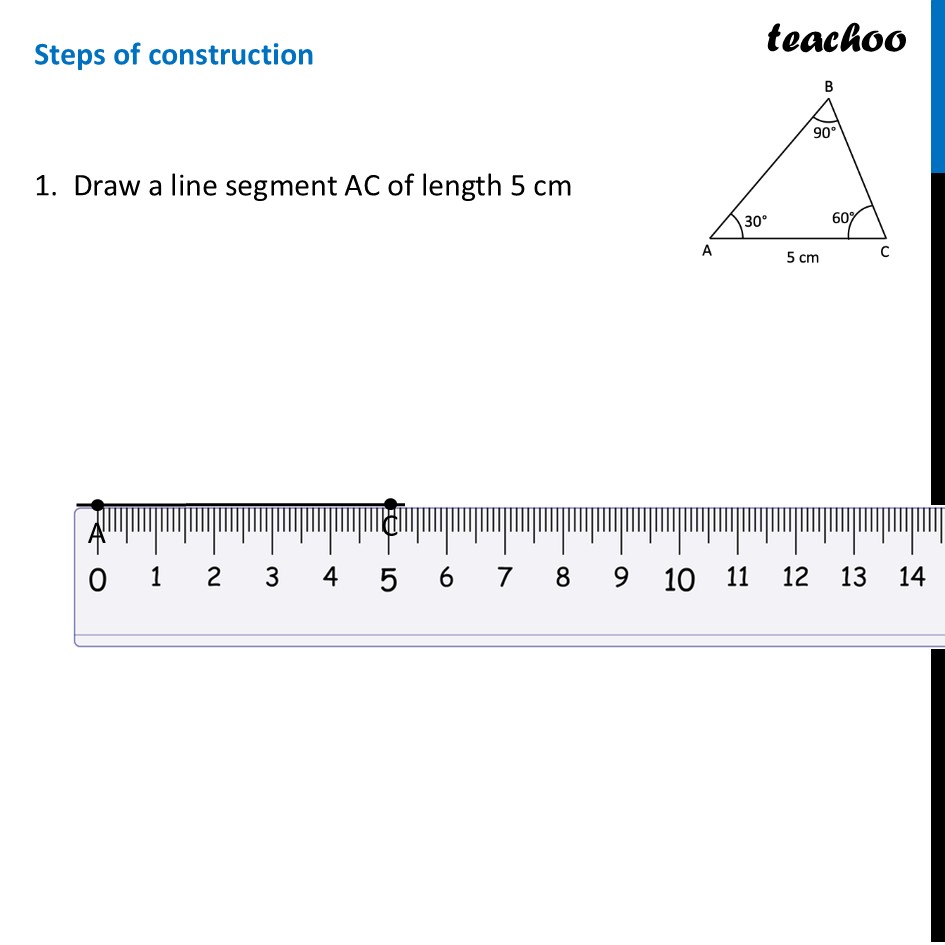
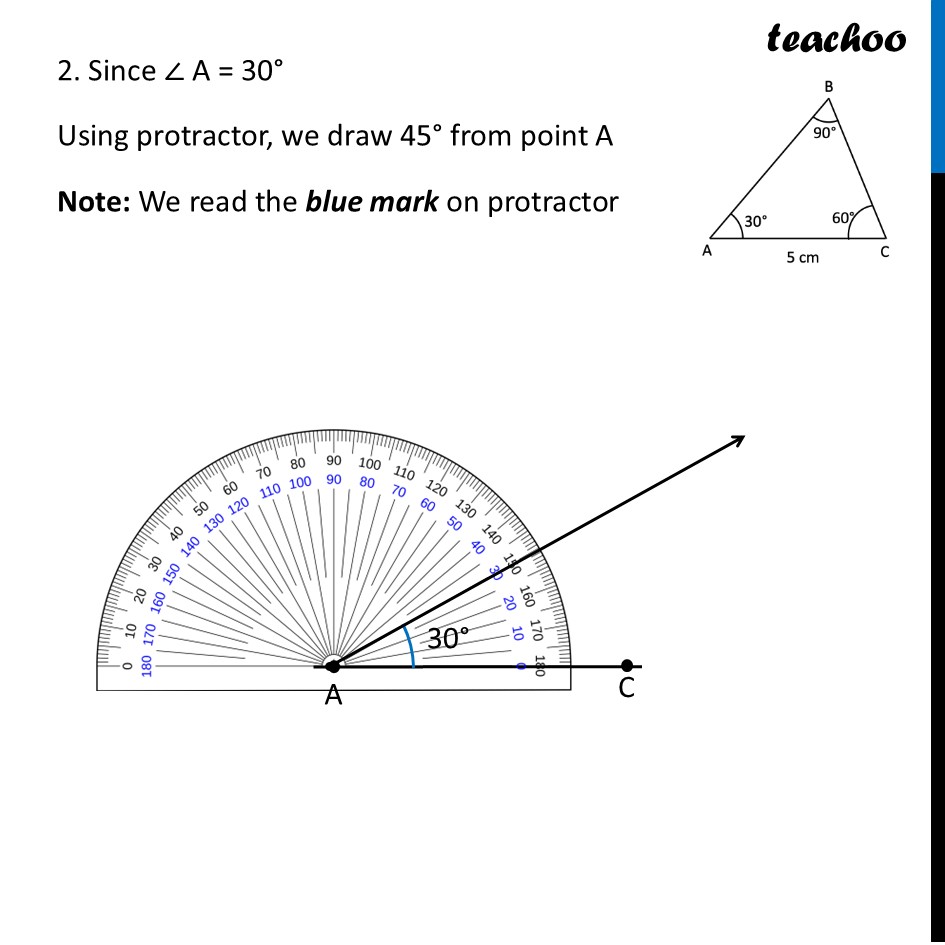
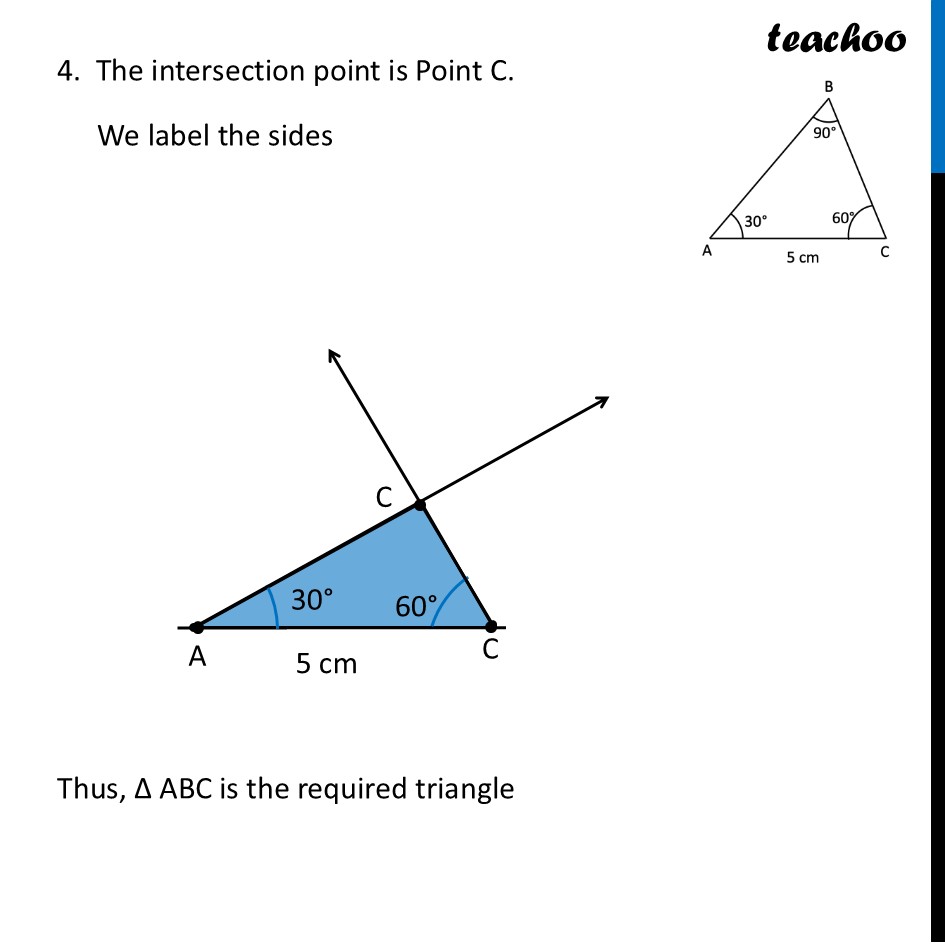
Question 3 Construct a right-angled triangle ∆ABC with ∠B = 90°, AC = 5 cm. How many different triangles exist with these measurements? [Hint: Note that the other measurements can take any values. Take AC as the base. What values can ∠A and ∠C take so that the other angle is 90°?] Let’s construct first Since ∠ B is 90°, we take BC as base We can take AB also – just point B has to be there Let’s draw Rough Diagram To construct this triangle, we need Both Angles - ∠ A & ∠ C Both Sides – AB & BC Let’s look at angles From Angle Sum Property ∠ A + ∠ B + ∠ C = 180° ∠ A + 90° + ∠ C = 180° ∠ A + ∠ C = 180° – 90° ∠ A + ∠ C = 90° Any two acute angles that add up to 90° will create a valid triangle. For example: If ∠ A = 30°, then ∠ C = 60°. This forms a valid triangle. If ∠ A = 45°, then ∠ C = 45°. This forms a different, valid triangle. If ∠ A = 70°, then ∠ C = 20°. This is another valid triangle. If ∠ A = 1°, then ∠ C = 89°. This is also a valid triangle. Since ∠ A can be any value greater than 0 and less than 90 (including decimals like $40.5), there are infinitely many different triangles that can exist with these measurements. Construction Let’s assume ∠ A = 30° & ∠ C = 60°. We already have ∠ B = 90° & AC = 5 cm Since AC is the only side we have. We use AC as Base So, our figure looks like Steps of construction 1. Draw a line segment AC of length 5 cm 2. Since ∠ A = 30° Using protractor, we draw 45° from point A Note: We read the blue mark on protractor 2. Since ∠ B = 80° Using protractor, we draw 80° from point B Note: We read the black mark on protractor 4. The intersection point is Point C. We label the sides Thus, Δ ABC is the required triangle