You are here
Altitudes of Triangles
Last updated at November 7, 2025 by Teachoo
Constructions Related to Altitudes of Triangles
Class 7 (Ganita Prakash & Old NCERT)
Chapter 7 Class 7 - A tale of three Intersecting Lines (Ganit Prakash)
- Definition
- Constructing Equilateral Triangle
- Constructing a Triangle when its Sides are given
- Figure it out - Page 150, 151
- Are Triangles Possible for any Lengths?
- Figure it out - Page 154
- Visualising the Construction of Circles
- Figure it out - Page 156
- Triangle Inequality & Construction of Circles
- Figure it out - Page 159
- Constructing Triangle when 2 Sides and the Included Angle are given
- Constructing Triangle when 2 Angles and the Included Side are given
- Do triangles always exist?
- Sum of angles of a triangle
- Angle Sum Property
- Exterior Angles
-
Constructions Related to Altitudes of Triangles
- Figure it out - Page 170, 171
Transcript
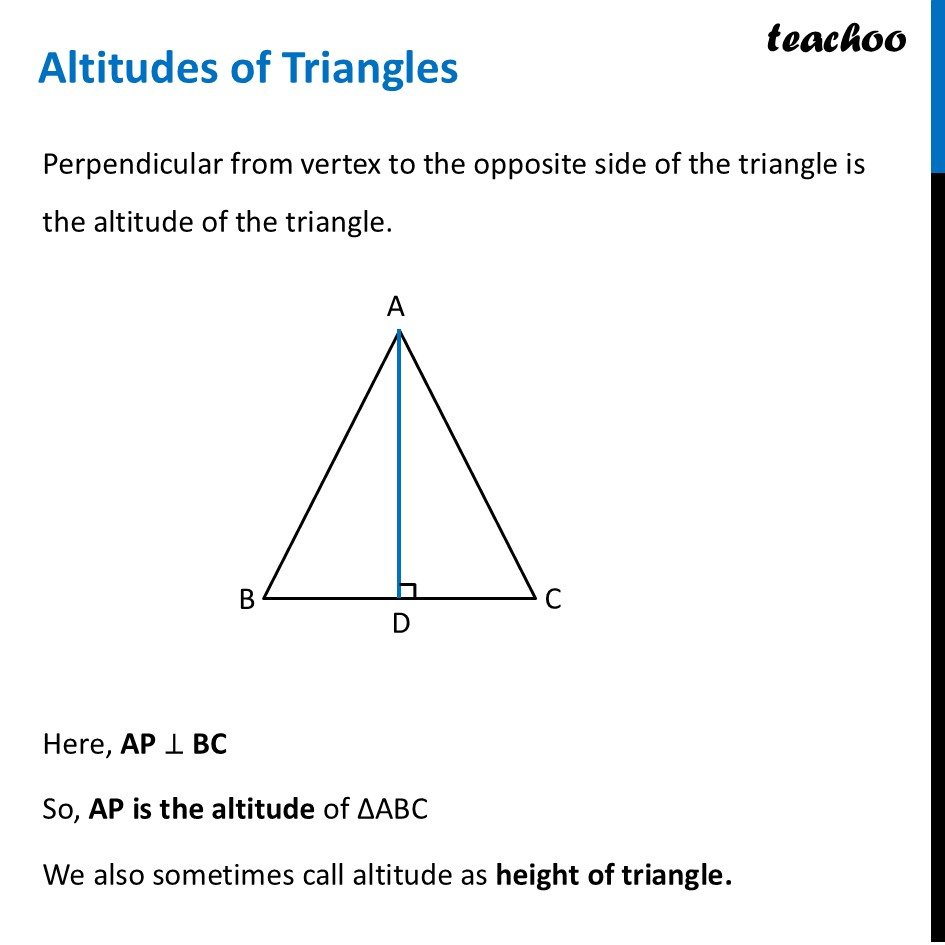
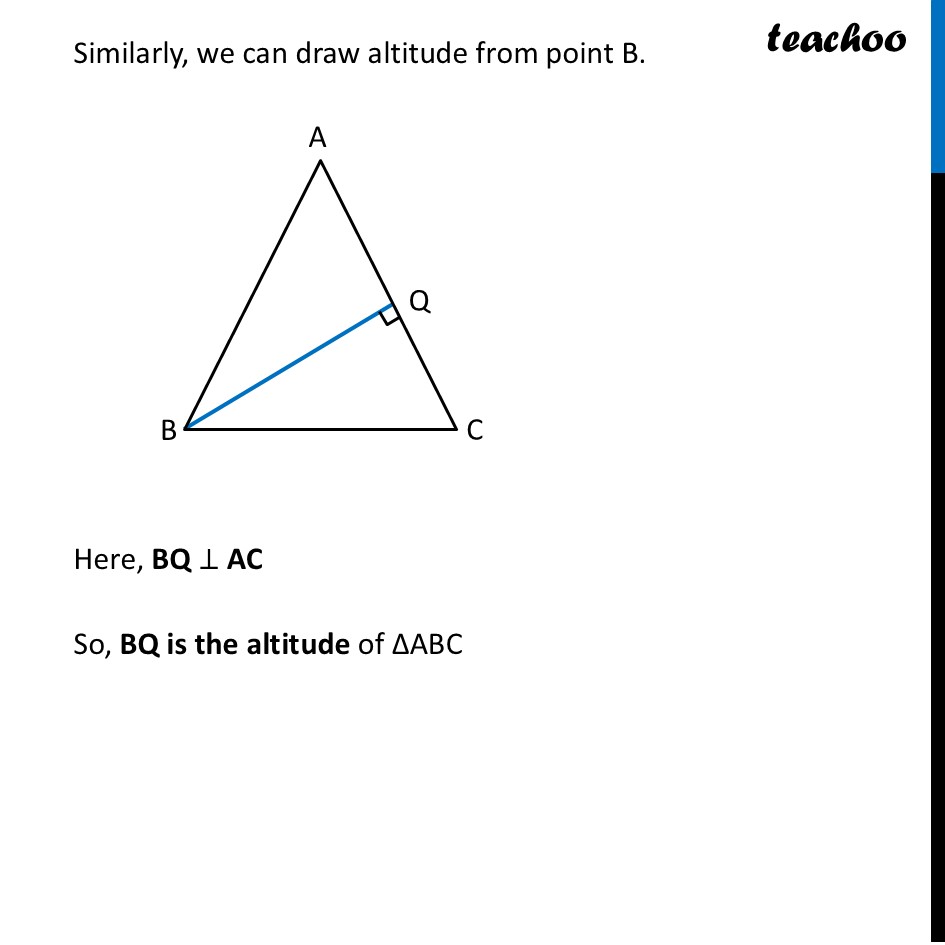
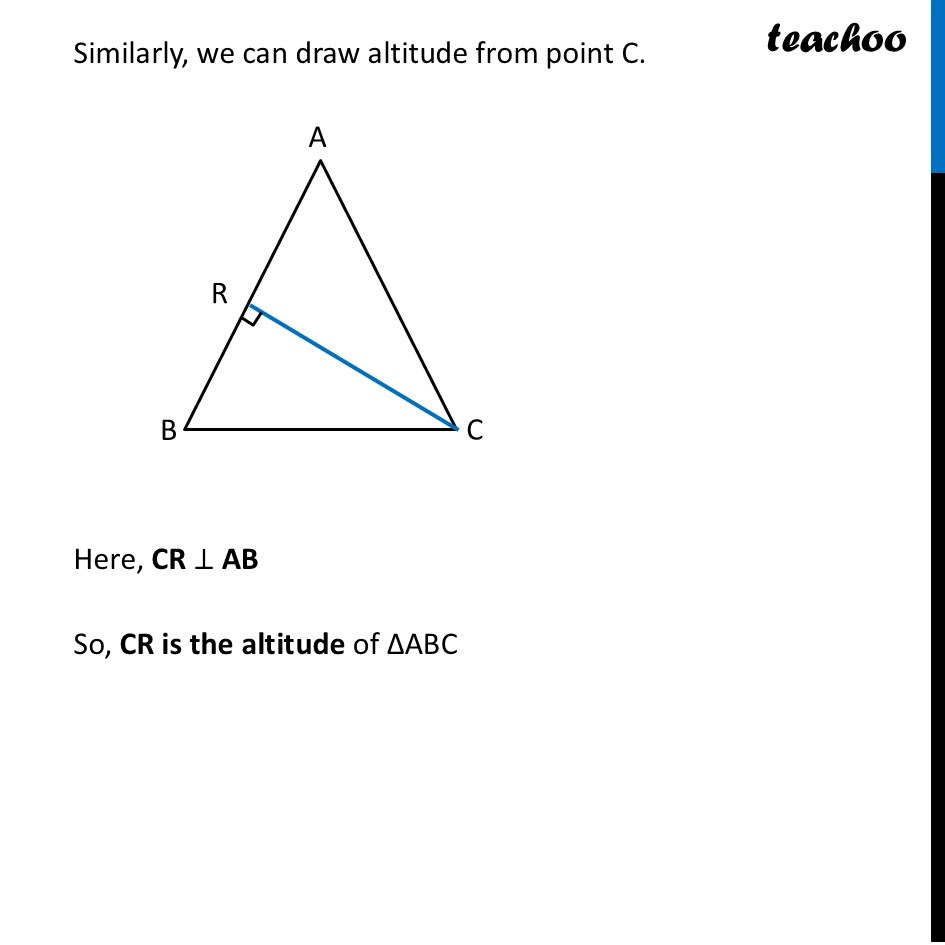
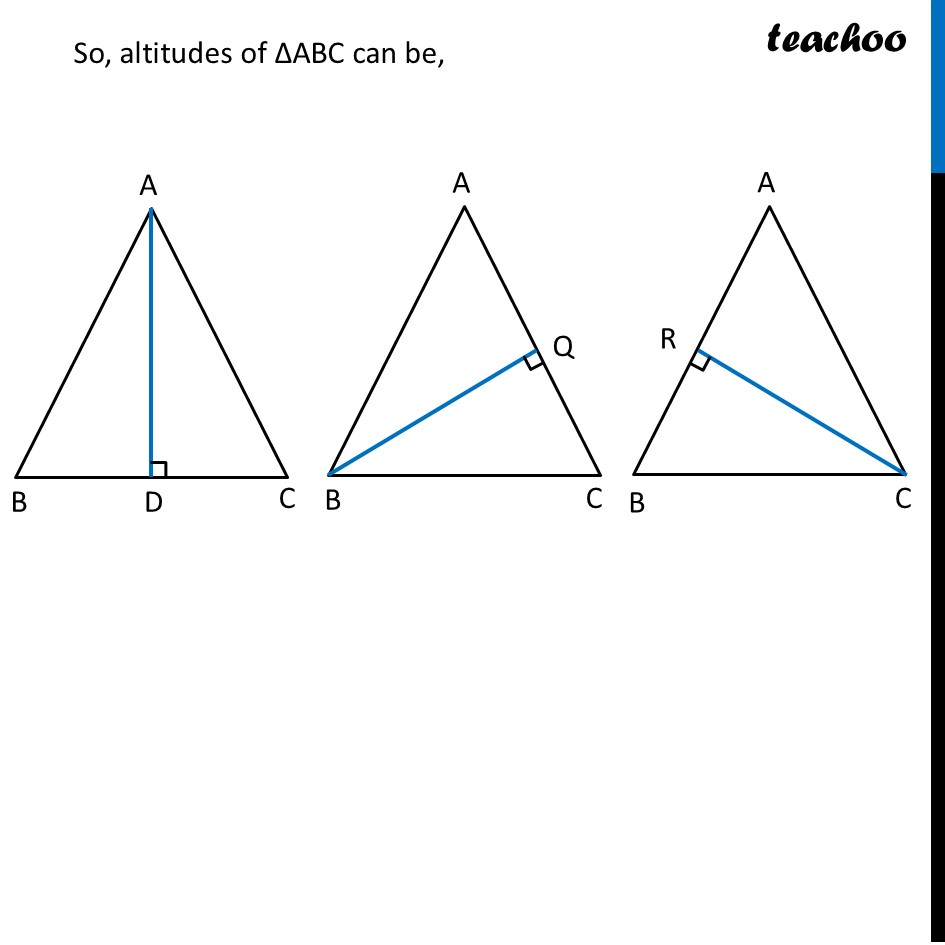
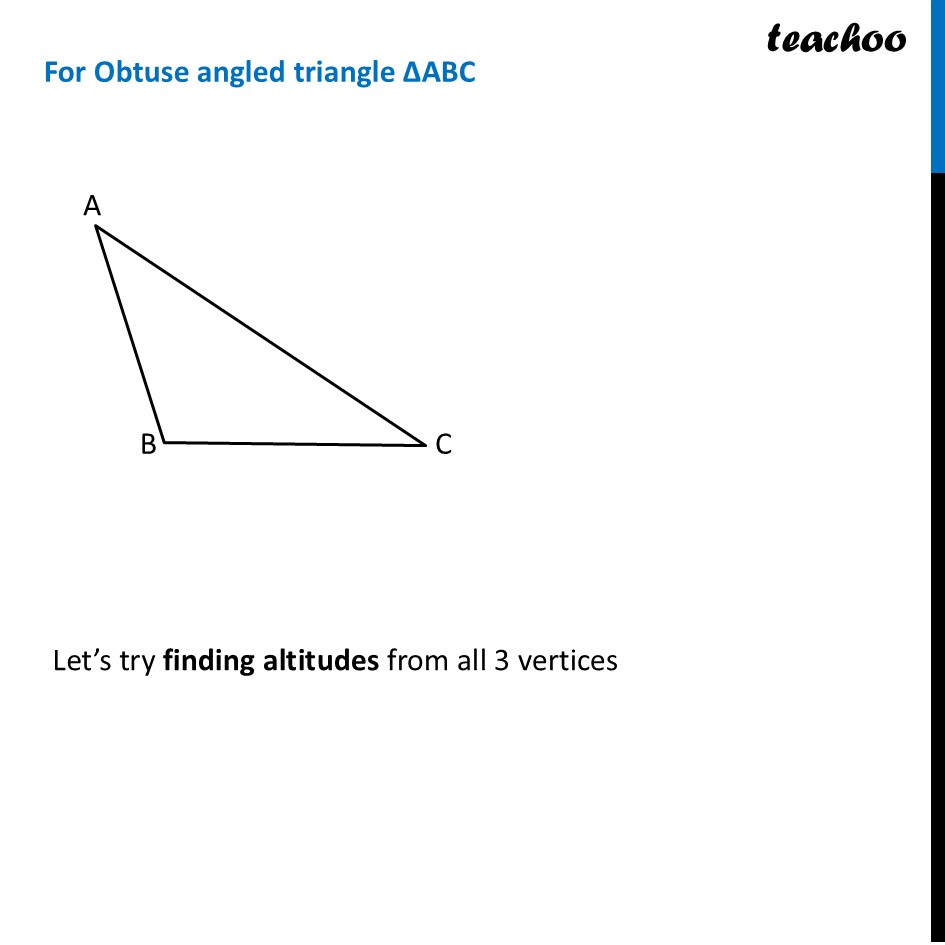
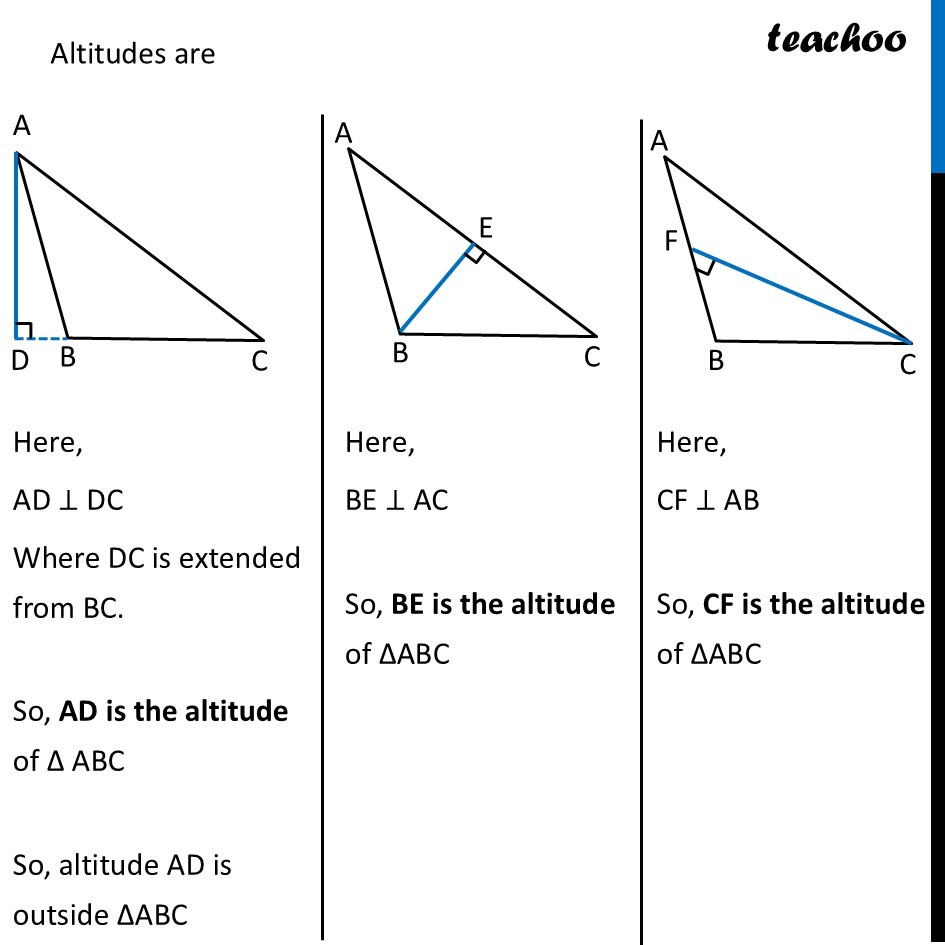
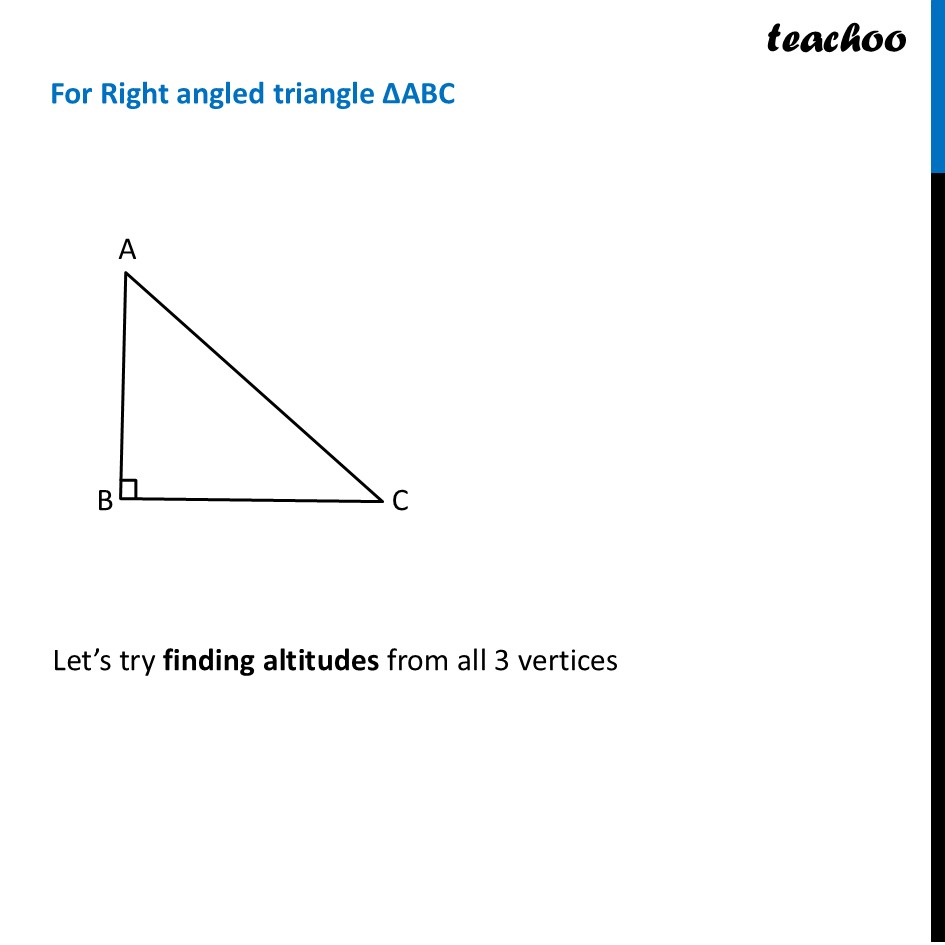
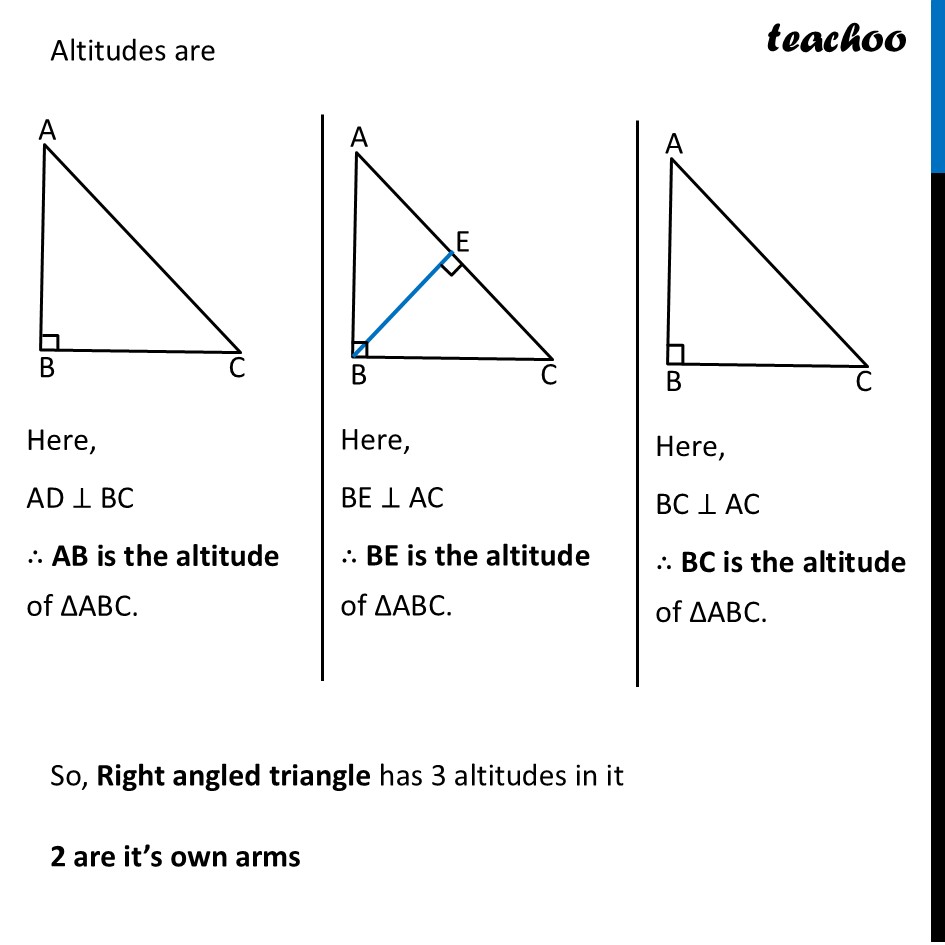
Altitudes of TrianglesPerpendicular from vertex to the opposite side of the triangle is the altitude of the triangle. Here, AP ⊥ BC So, AP is the altitude of ∆ABC We also sometimes call altitude as height of triangle. Similarly, we can draw altitude from point B. Here, BQ ⊥ AC So, BQ is the altitude of ∆ABC Similarly, we can draw altitude from point C. Here, CR ⊥ AB So, CR is the altitude of ∆ABC So, altitudes of ∆ABC can be, For Obtuse angled triangle ∆ABC Let’s try finding altitudes from all 3 vertices Altitudes are Here, AD ⊥ DC Where DC is extended from BC. So, AD is the altitude of ∆ ABC So, altitude AD is outside ∆ABC Here, BE ⊥ AC So, BE is the altitude of ∆ABC Here, CF ⊥ AB So, CF is the altitude of ∆ABC For Right angled triangle ∆ABC Let’s try finding altitudes from all 3 vertices Altitudes are So, Right angled triangle has 3 altitudes in it 2 are it’s own arms Here, AD ⊥ BC ∴ AB is the altitude of ∆ABC. Here, BE ⊥ AC ∴ BE is the altitude of ∆ABC. Here, BC ⊥ AC ∴ BC is the altitude of ∆ABC.
