Question 1 - Figure it out - Page 165 - Sum of angles of a triangle - Chapter 7 Class 7 - A tale of three Intersecting Lines (Ganit Prakash)

Transcript

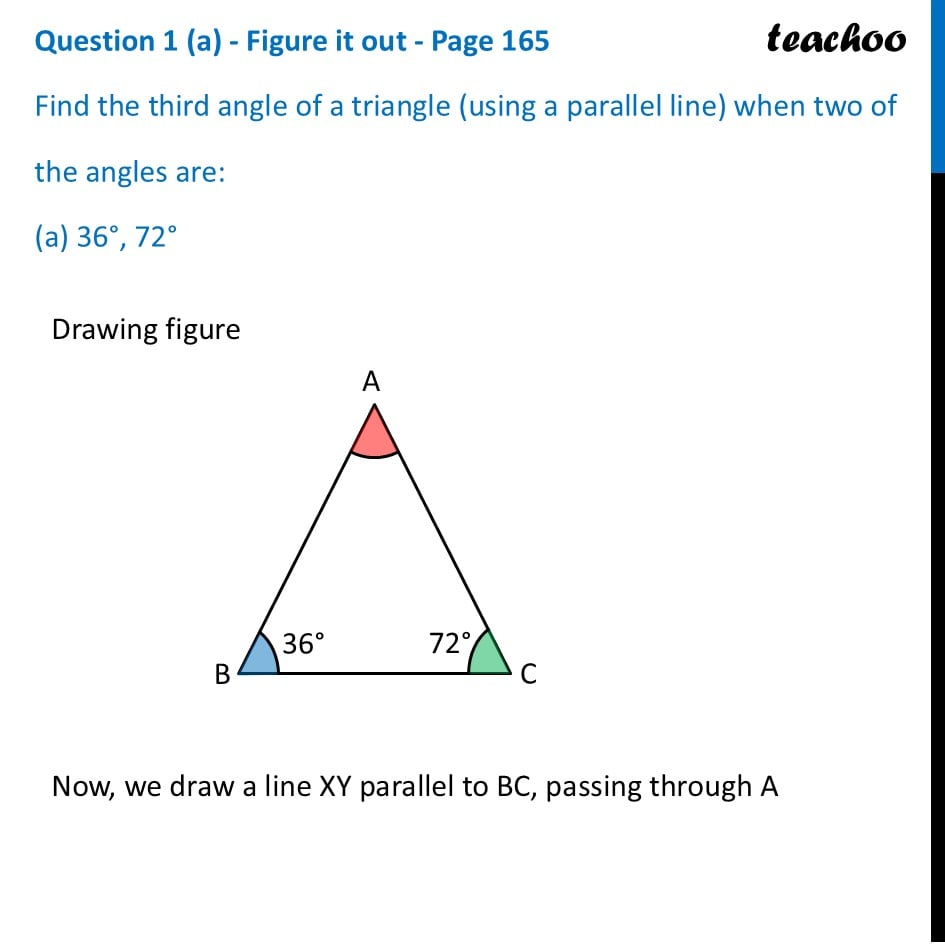
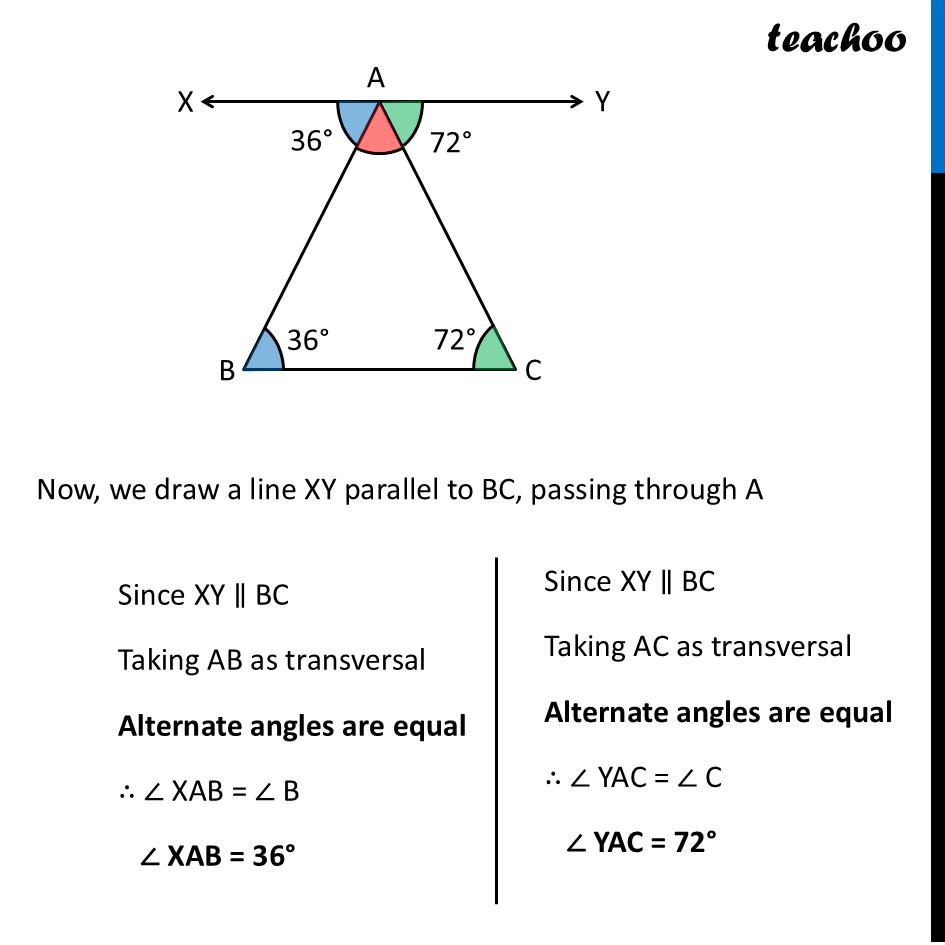
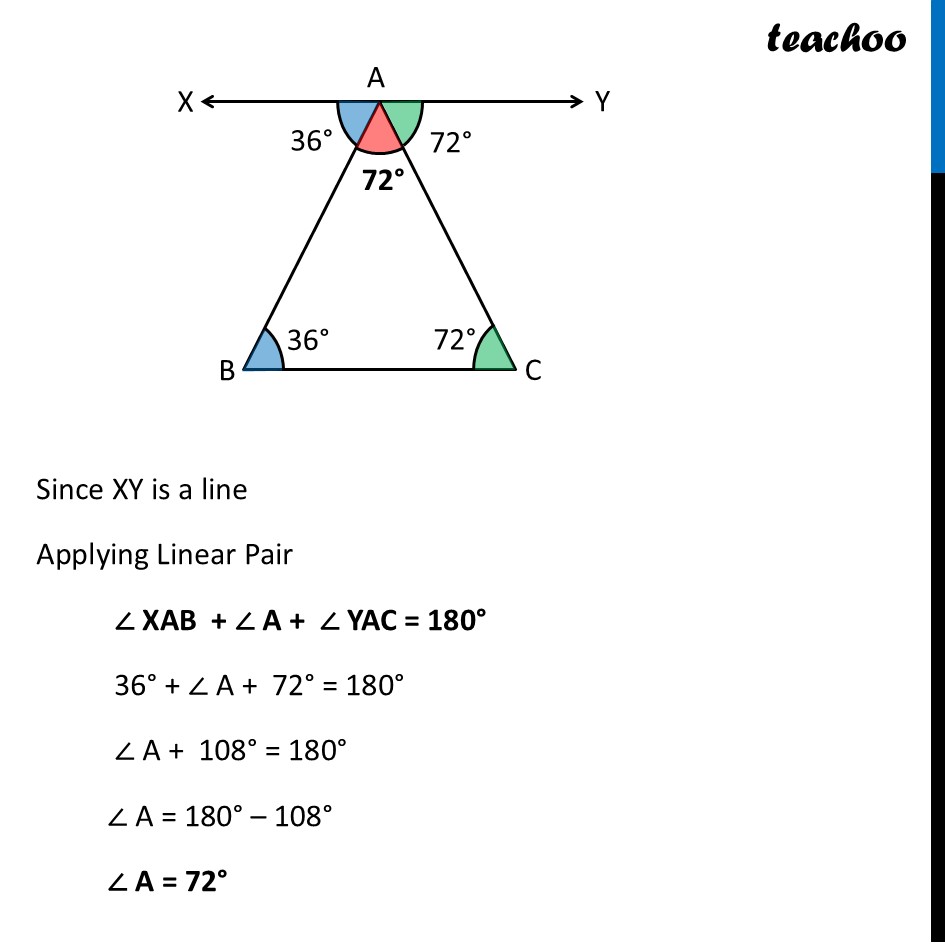
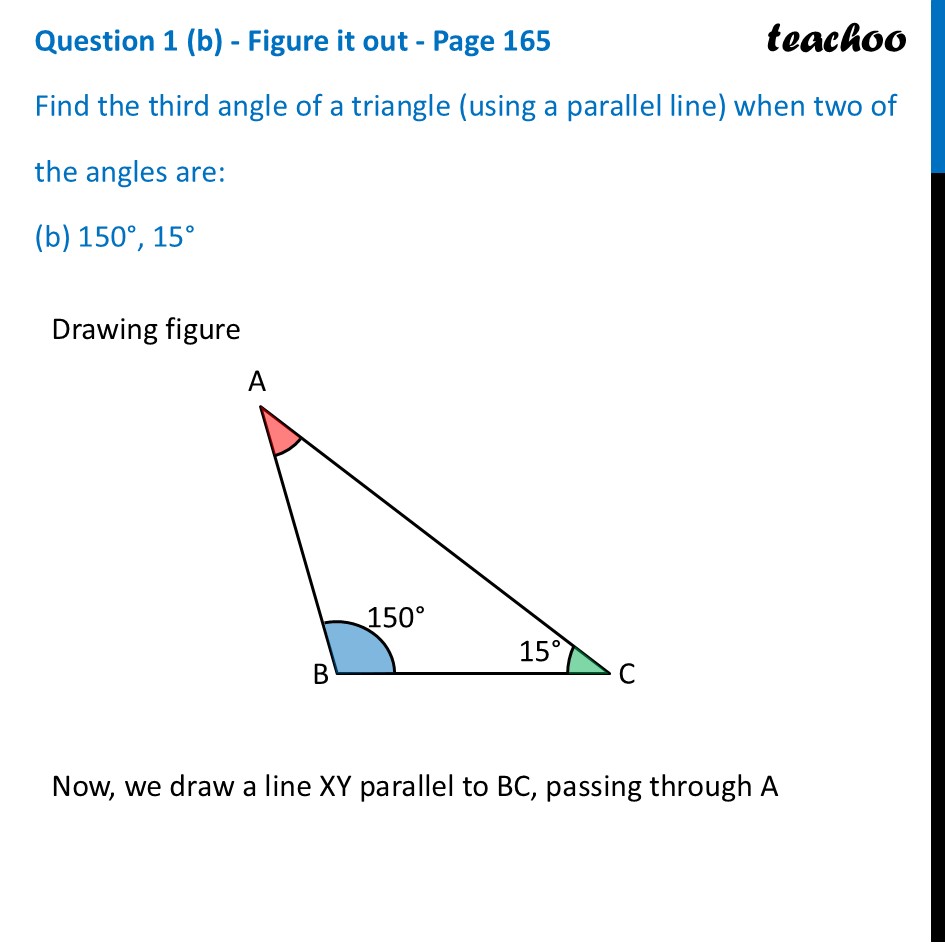
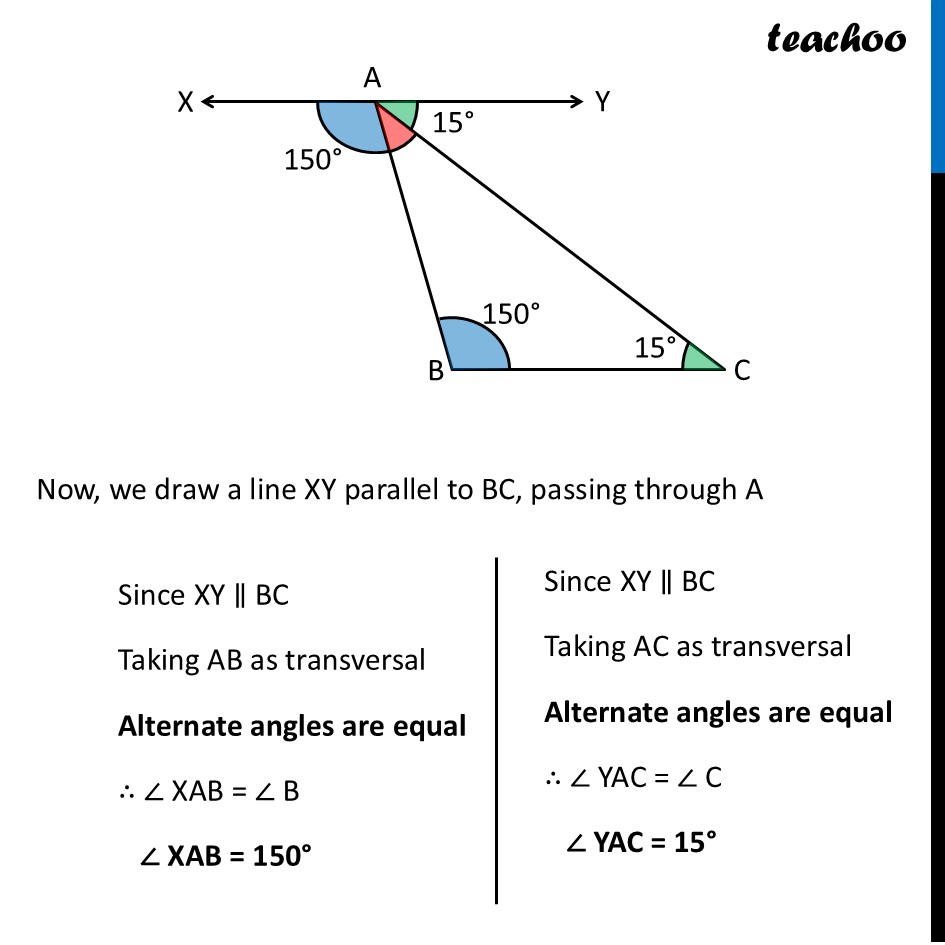
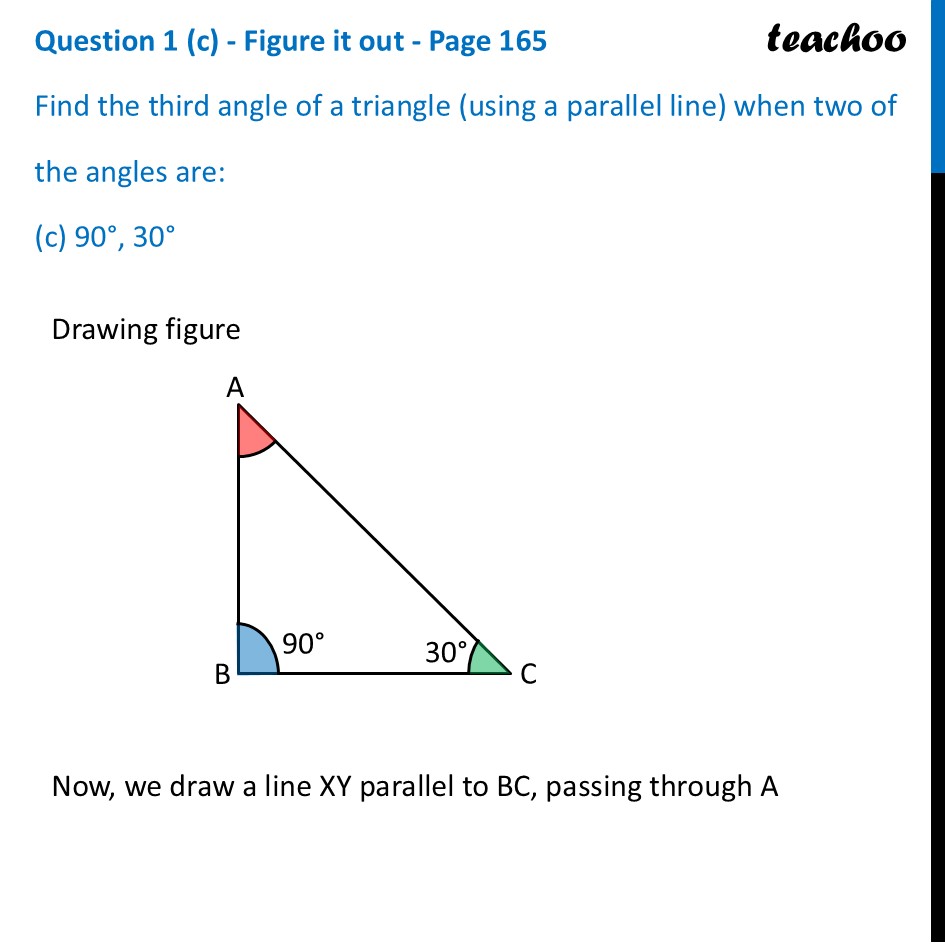
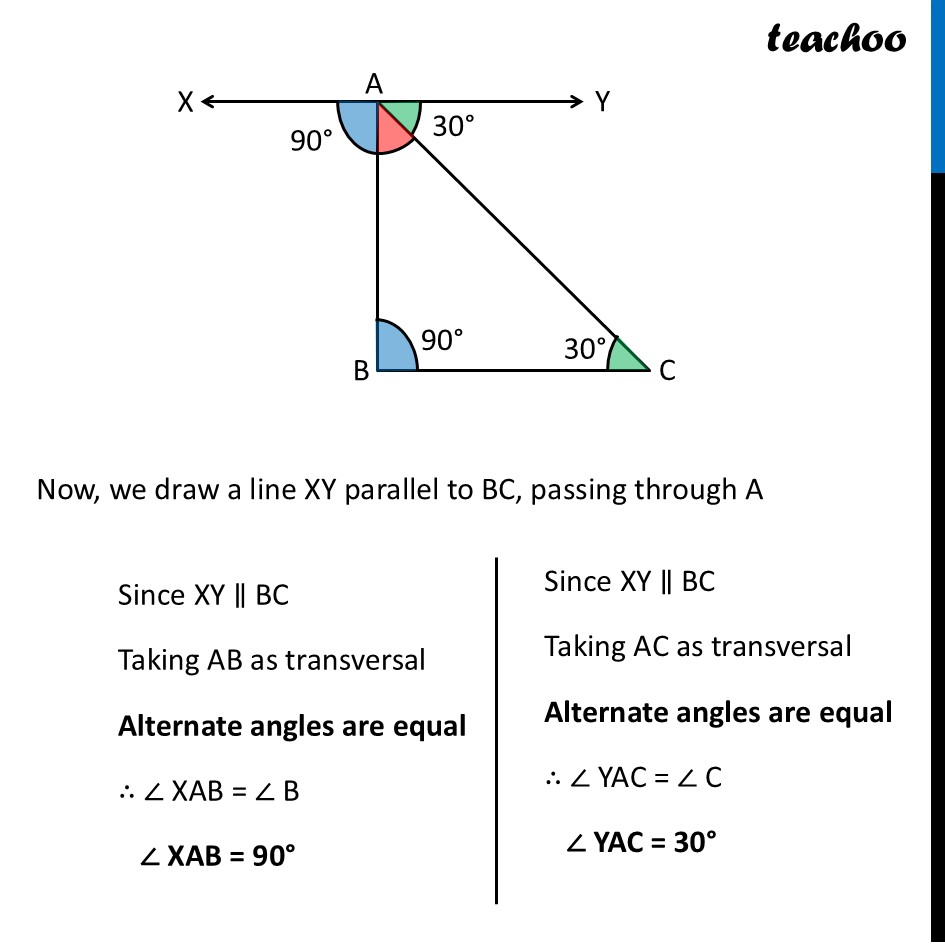
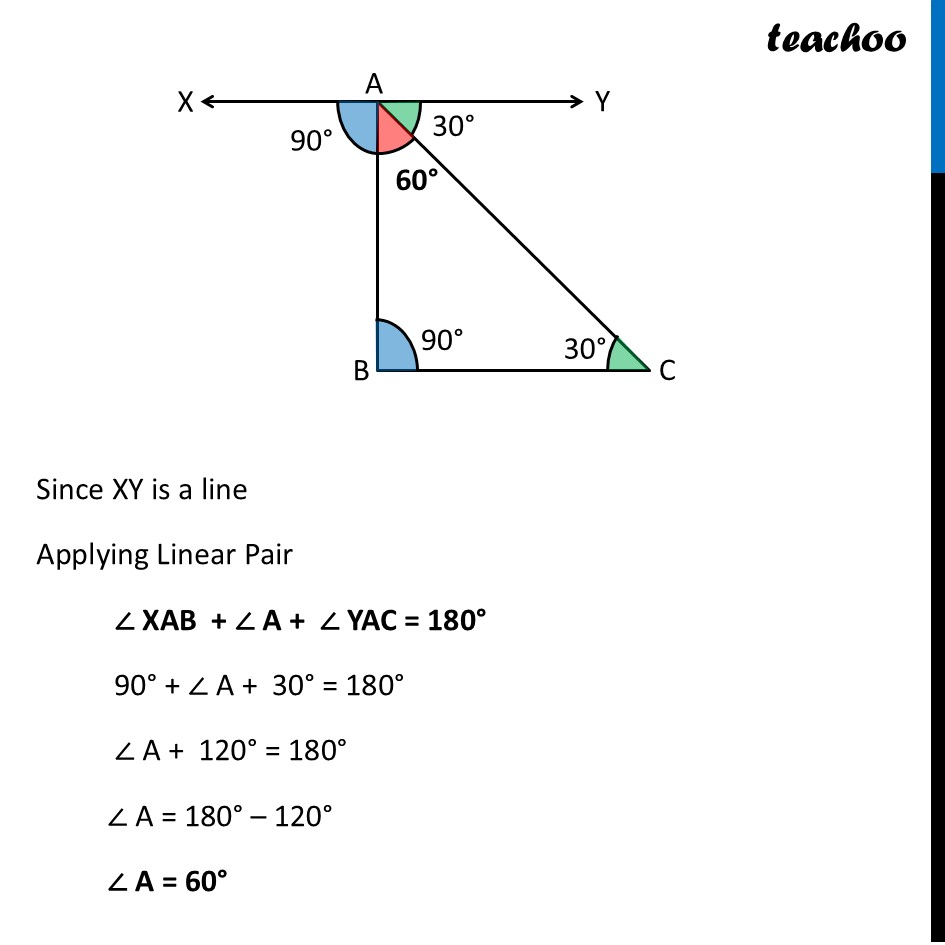
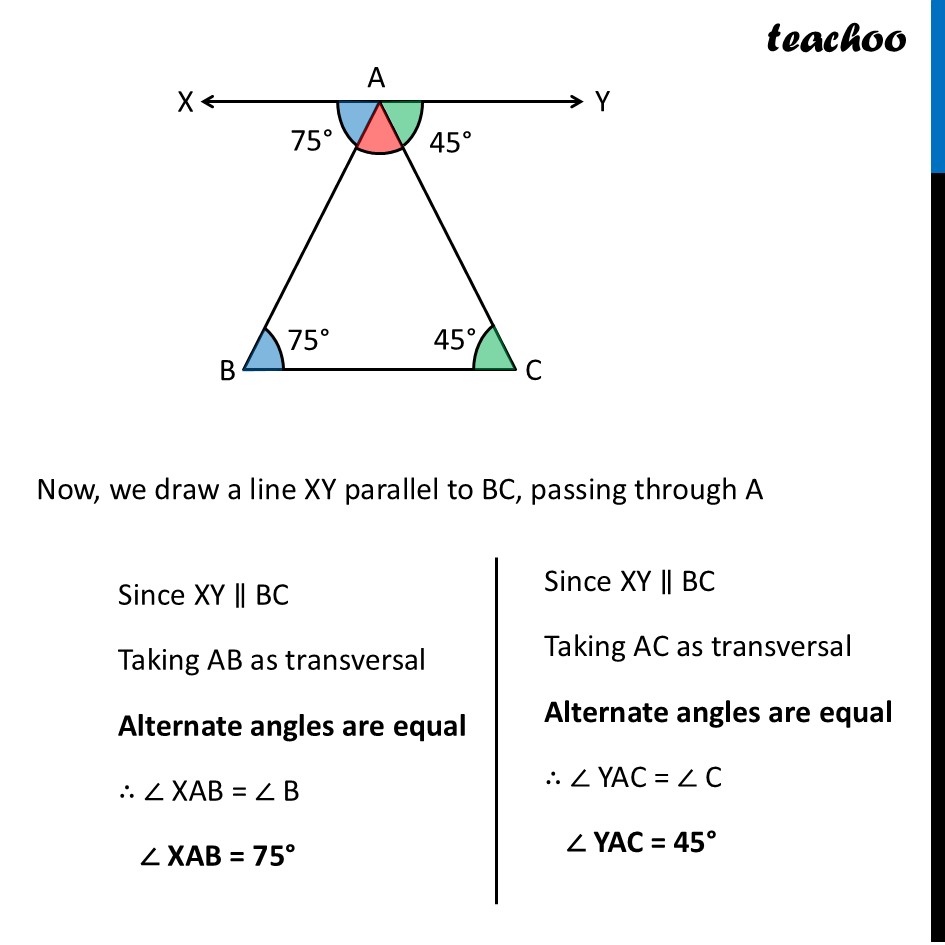
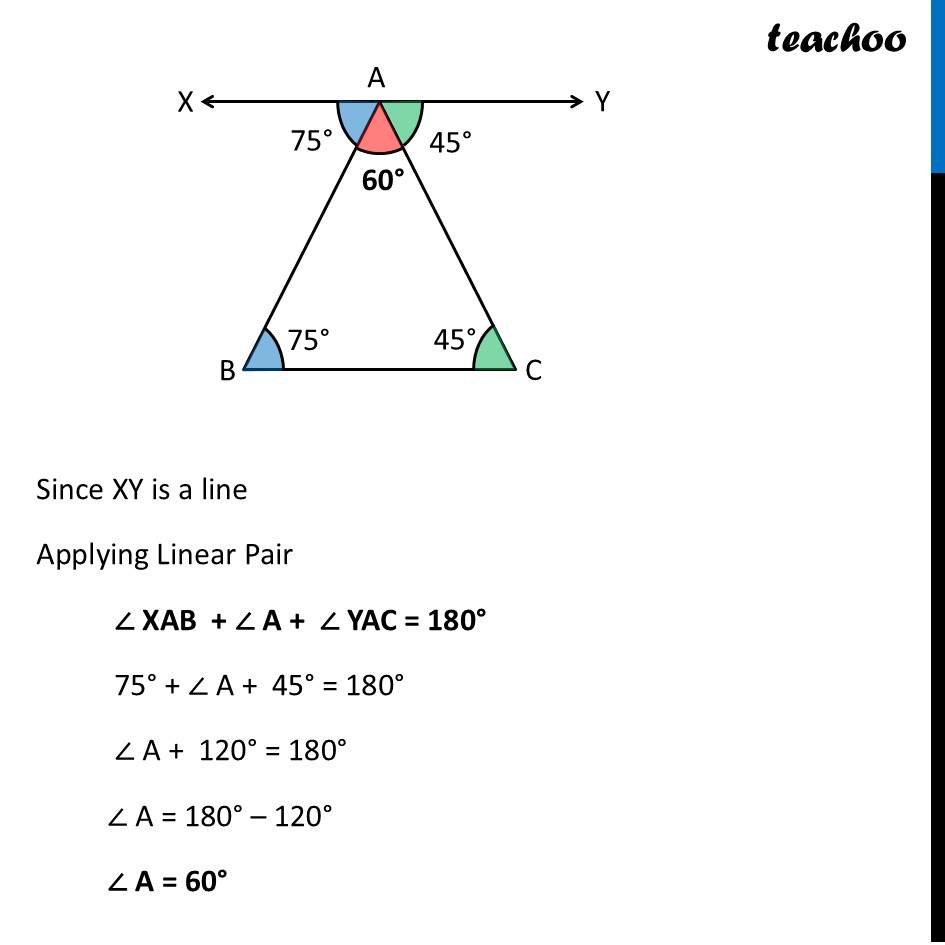
Question 1 (a) - Figure it out - Page 165 Find the third angle of a triangle (using a parallel line) when two of the angles are: (a) 36°, 72° Drawing figure Now, we draw a line XY parallel to BC, passing through A Now, we draw a line XY parallel to BC, passing through A Since XY ∥ BC Taking AB as transversal Alternate angles are equal ∴ ∠ XAB = ∠ B ∠ XAB = 36° Since XY ∥ BC Taking AC as transversal Alternate angles are equal ∴ ∠ YAC = ∠ C ∠ YAC = 72° Since XY is a line Applying Linear Pair ∠ XAB + ∠ A + ∠ YAC = 180° 36° + ∠ A + 72° = 180° ∠ A + 108° = 180° ∠ A = 180° – 108° ∠ A = 72° Question 1 (b) - Figure it out - Page 165 Find the third angle of a triangle (using a parallel line) when two of the angles are: (b) 150°, 15° Drawing figure Now, we draw a line XY parallel to BC, passing through A Now, we draw a line XY parallel to BC, passing through A Since XY ∥ BC Taking AB as transversal Alternate angles are equal ∴ ∠ XAB = ∠ B ∠ XAB = 150° Since XY ∥ BC Taking AC as transversal Alternate angles are equal ∴ ∠ YAC = ∠ C ∠ YAC = 15° Since XY is a line Applying Linear Pair ∠ XAB + ∠ A + ∠ YAC = 180° 150° + ∠ A + 15° = 180° ∠ A + 165° = 180° ∠ A = 180° – 165° ∠ A = 15° Question 1 (c) - Figure it out - Page 165 Find the third angle of a triangle (using a parallel line) when two of the angles are: (c) 90°, 30° Drawing figure Now, we draw a line XY parallel to BC, passing through A Now, we draw a line XY parallel to BC, passing through A Since XY ∥ BC Taking AB as transversal Alternate angles are equal ∴ ∠ XAB = ∠ B ∠ XAB = 90° Since XY ∥ BC Taking AC as transversal Alternate angles are equal ∴ ∠ YAC = ∠ C ∠ YAC = 30° Since XY is a line Applying Linear Pair ∠ XAB + ∠ A + ∠ YAC = 180° 90° + ∠ A + 30° = 180° ∠ A + 120° = 180° ∠ A = 180° – 120° ∠ A = 60° Question 1 (d) - Figure it out - Page 165 Find the third angle of a triangle (using a parallel line) when two of the angles are: (d) 75°, 45° Drawing figure Now, we draw a line XY parallel to BC, passing through A Now, we draw a line XY parallel to BC, passing through A Since XY ∥ BC Taking AB as transversal Alternate angles are equal ∴ ∠ XAB = ∠ B ∠ XAB = 75° Since XY ∥ BC Taking AC as transversal Alternate angles are equal ∴ ∠ YAC = ∠ C ∠ YAC = 45° Since XY is a line Applying Linear Pair ∠ XAB + ∠ A + ∠ YAC = 180° 75° + ∠ A + 45° = 180° ∠ A + 120° = 180° ∠ A = 180° – 120° ∠ A = 60°