You are here
Question 2 - Page 153 - Are Triangles Possible for any Lengths? - Chapter 7 Class 7 - A tale of three Intersecting Lines (Ganit Prakash)
Last updated at November 5, 2025 by Teachoo
Class 7 (Ganita Prakash & Old NCERT)
Chapter 7 Class 7 - A tale of three Intersecting Lines (Ganit Prakash)
- Definition
- Constructing Equilateral Triangle
- Constructing a Triangle when its Sides are given
- Figure it out - Page 150, 151
-
Are Triangles Possible for any Lengths?
- Figure it out - Page 154
- Visualising the Construction of Circles
- Figure it out - Page 156
- Triangle Inequality & Construction of Circles
- Figure it out - Page 159
- Constructing Triangle when 2 Sides and the Included Angle are given
- Constructing Triangle when 2 Angles and the Included Side are given
- Do triangles always exist?
- Sum of angles of a triangle
- Angle Sum Property
- Exterior Angles
- Constructions Related to Altitudes of Triangles
- Figure it out - Page 170, 171
Transcript
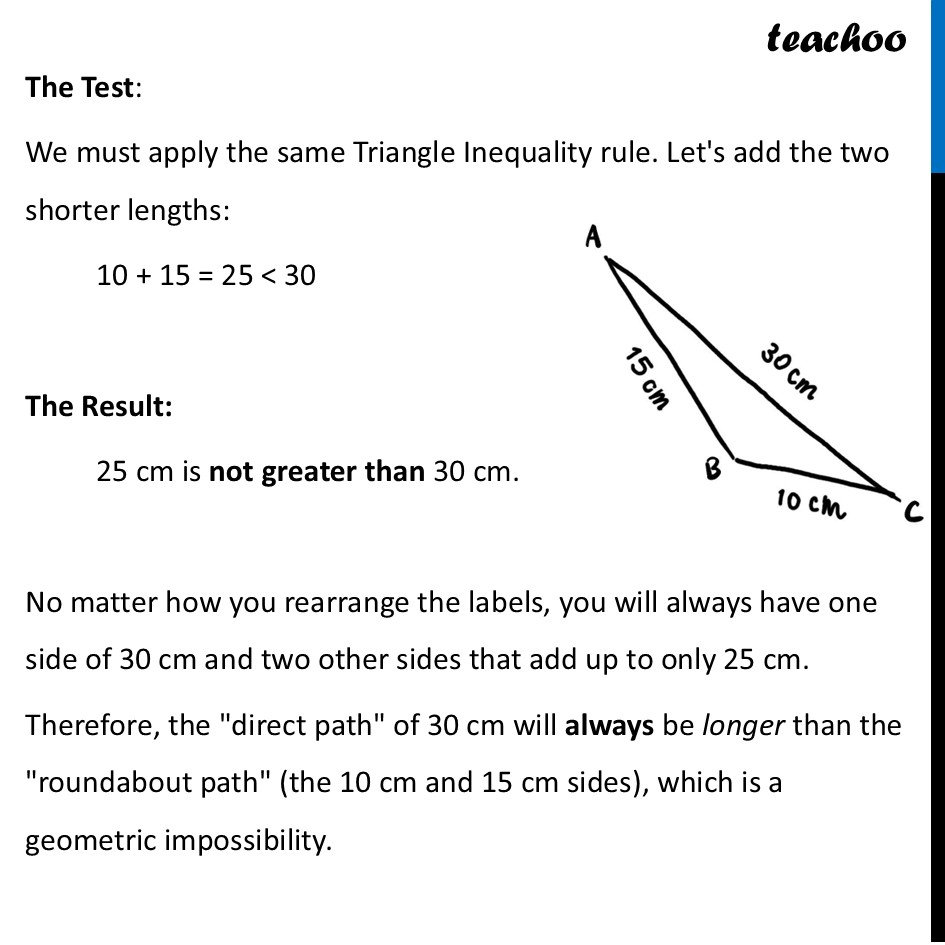
Question 2 - Page 153 “In the rough diagram in Fig. 7.4, is it possible to assign lengths in a different order such that the direct paths are always coming out to be shorter than the roundabout paths? If this is possible, then a triangle might exist.” Is such rearrangement of lengths possible in the triangle? No, such a rearrangement is not possible. Here is the detailed explanation: The Problem: The issue is not with how the lengths are assigned (e.g., AB=15, BC=10, AC=30). The issue is with the set of lengths {10, 15, 30} itself. The Test: We must apply the same Triangle Inequality rule. Let's add the two shorter lengths: 10 + 15 = 25 < 30 The Result: 25 cm is not greater than 30 cm. No matter how you rearrange the labels, you will always have one side of 30 cm and two other sides that add up to only 25 cm. Therefore, the "direct path" of 30 cm will always be longer than the "roundabout path" (the 10 cm and 15 cm sides), which is a geometric impossibility.
