You are here
![Triangle Inequality - Visualised with Example [Class 7 Ganita Prakash] - Are Triangles Possible for any Lengths?](https://cdn.teachoo.com/01599a69-e911-49f0-a3f1-ef409dc78f27/slide82.jpg)
Triangle Inequality
Last updated at November 5, 2025 by Teachoo
Class 7 (Ganita Prakash & Old NCERT)
Chapter 7 Class 7 - A tale of three Intersecting Lines (Ganit Prakash)
- Definition
- Constructing Equilateral Triangle
- Constructing a Triangle when its Sides are given
- Figure it out - Page 150, 151
-
Are Triangles Possible for any Lengths?
- Figure it out - Page 154
- Visualising the Construction of Circles
- Figure it out - Page 156
- Triangle Inequality & Construction of Circles
- Figure it out - Page 159
- Constructing Triangle when 2 Sides and the Included Angle are given
- Constructing Triangle when 2 Angles and the Included Side are given
- Do triangles always exist?
- Sum of angles of a triangle
- Angle Sum Property
- Exterior Angles
- Constructions Related to Altitudes of Triangles
- Figure it out - Page 170, 171
Transcript
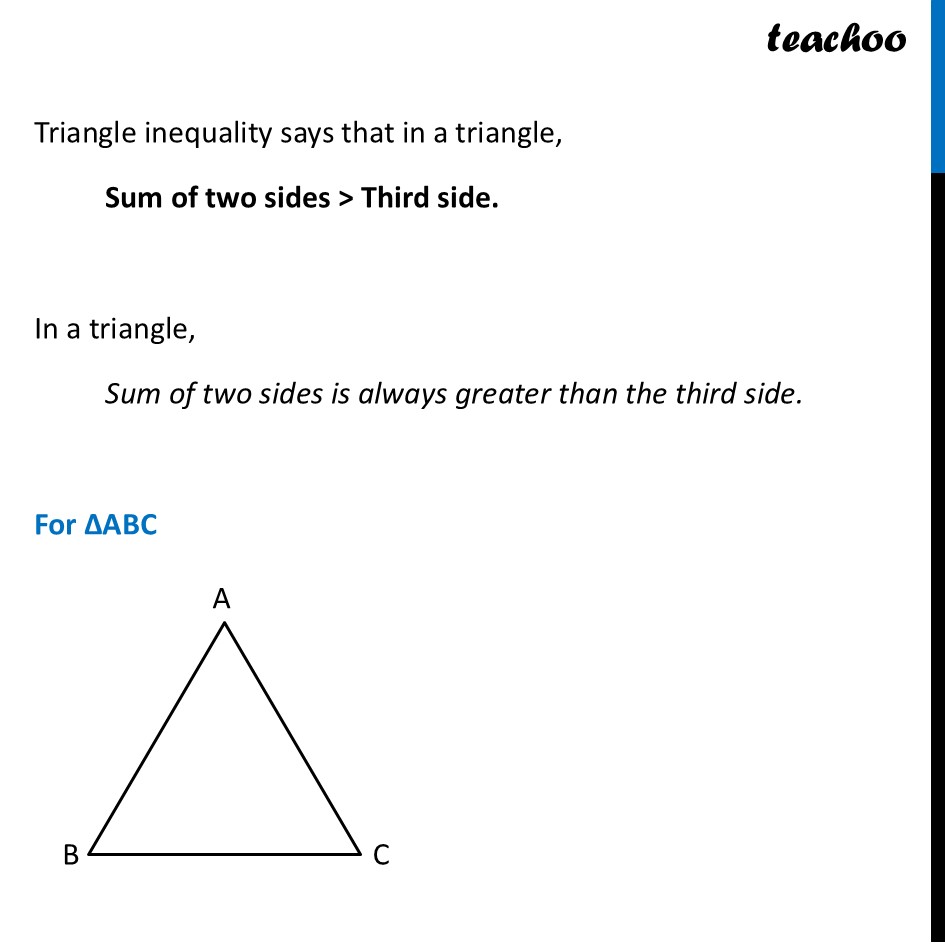
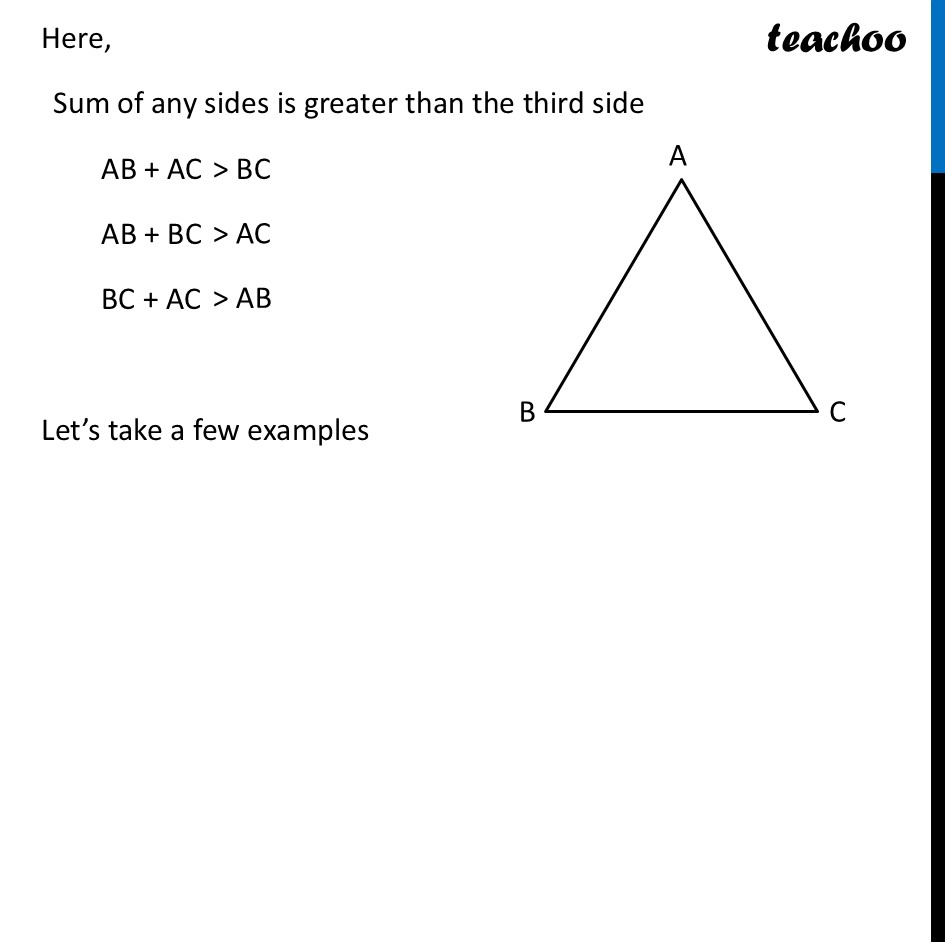
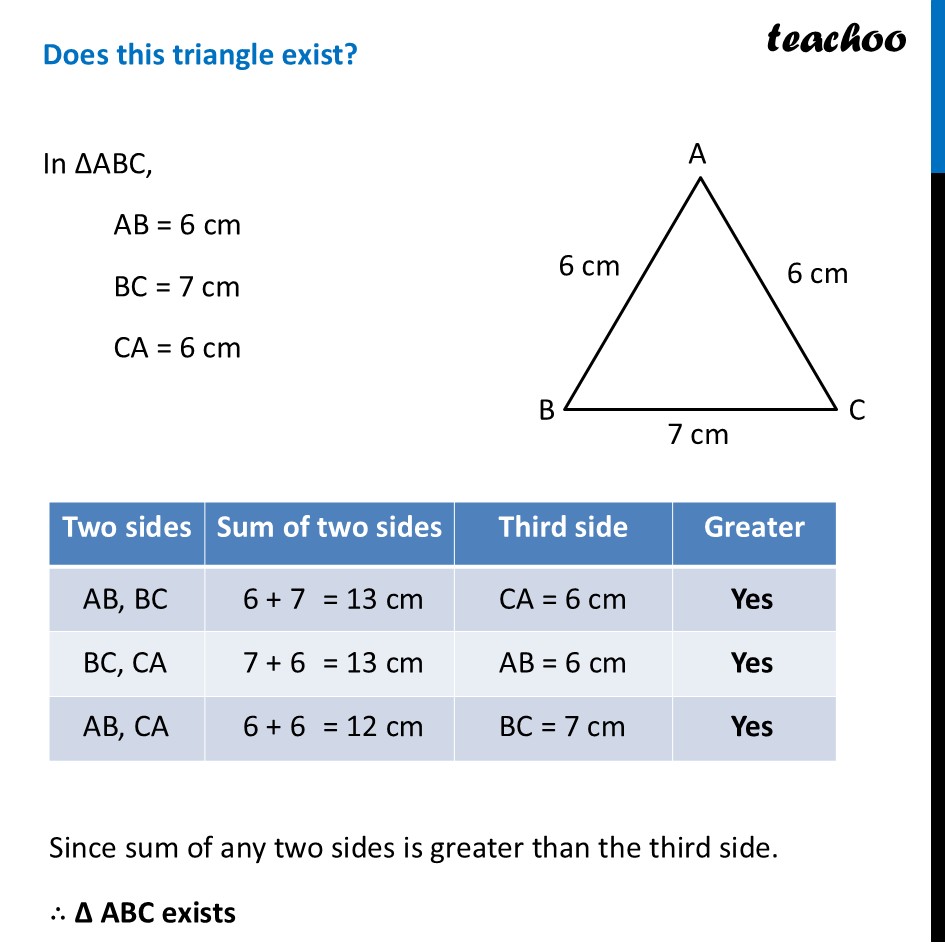
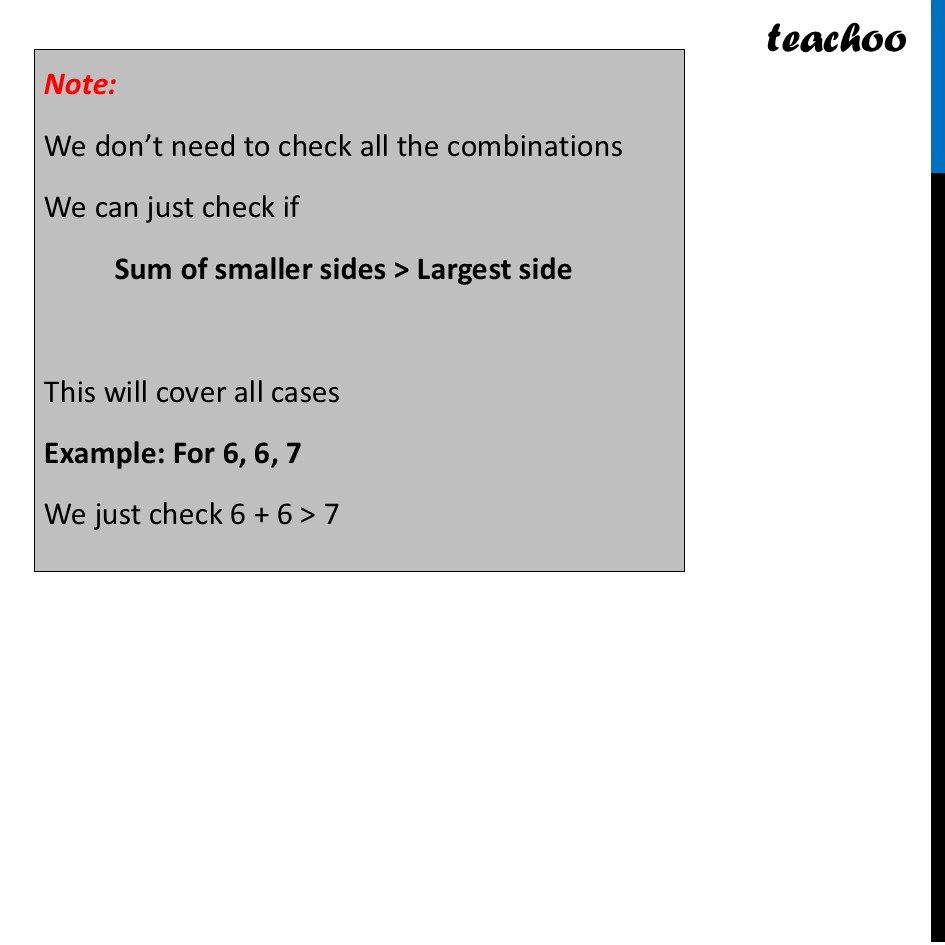
Triangle InequalityTriangle Inequality says that for a triangle to form, this must be true Triangle inequality says that in a triangle, Sum of two sides > Third side. In a triangle, Sum of two sides is always greater than the third side. For ∆ABC Here, Sum of any sides is greater than the third side AB + AC AB + BC BC + AC Let’s take a few examples Does this triangle exist? In ∆ABC, AB = 6 cm BC = 7 cm CA = 6 cm Since sum of any two sides is greater than the third side. ∴ ∆ ABC exists Note: We don’t need to check all the combinations We can just check if Sum of smaller sides > Largest side This will cover all cases Example: For 6, 6, 7 We just check 6 + 6 > 7
