Question 2 - Figure it out - Page 150, 151 - Chapter 7 Class 7 - A tale of three Intersecting Lines (Ganit Prakash)

Transcript

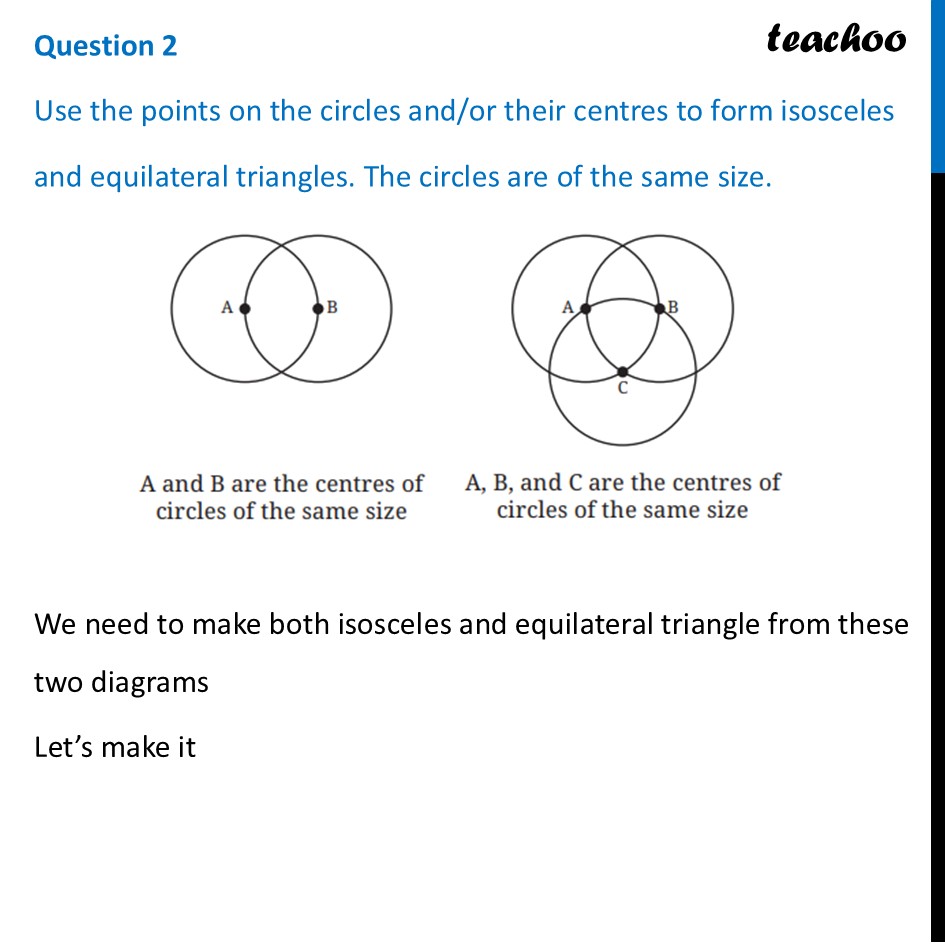
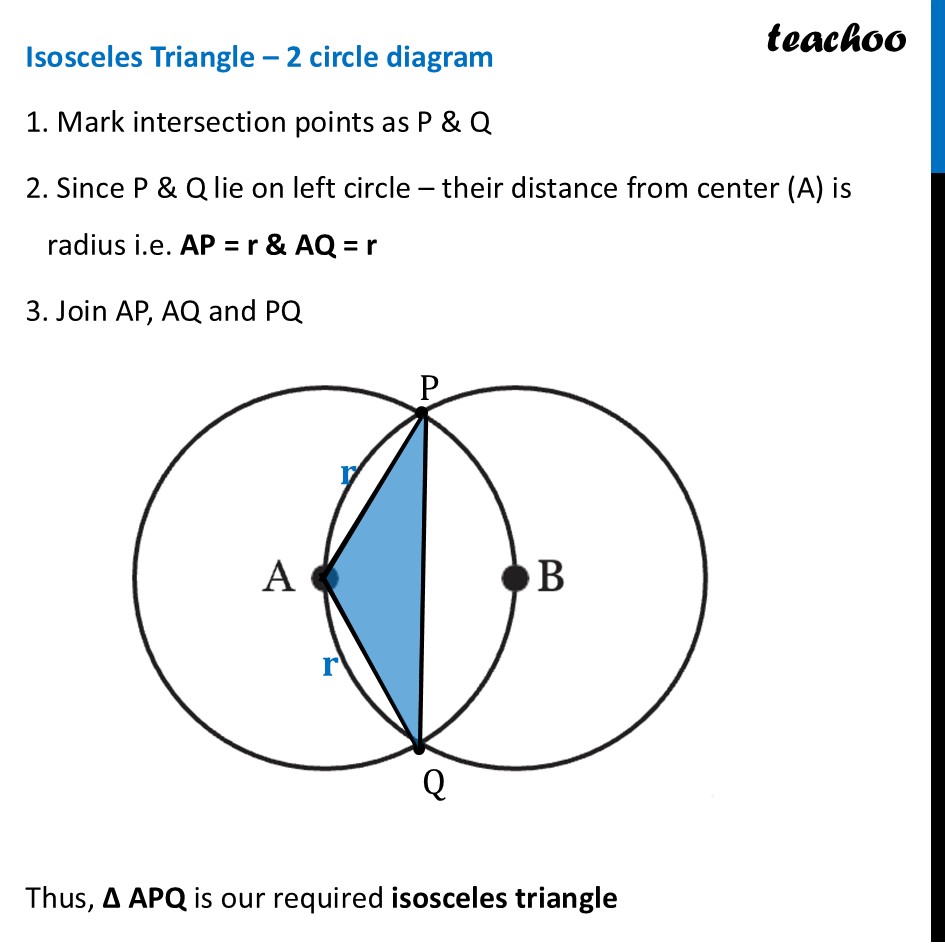
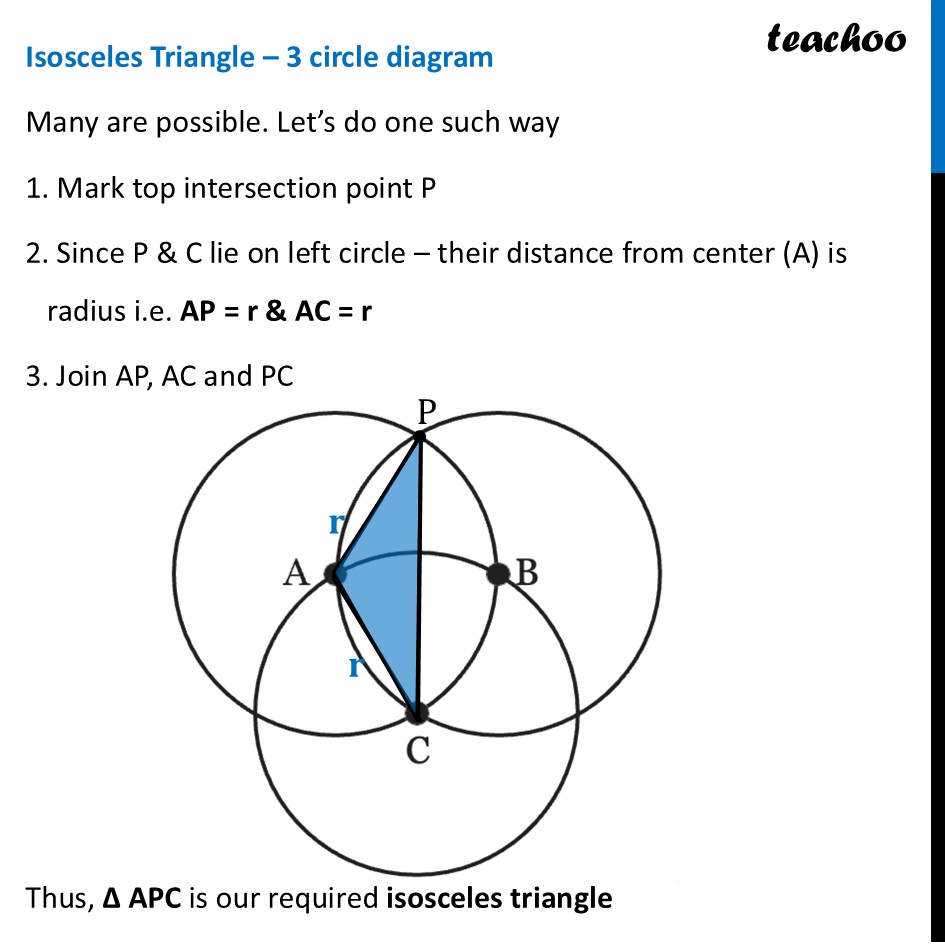
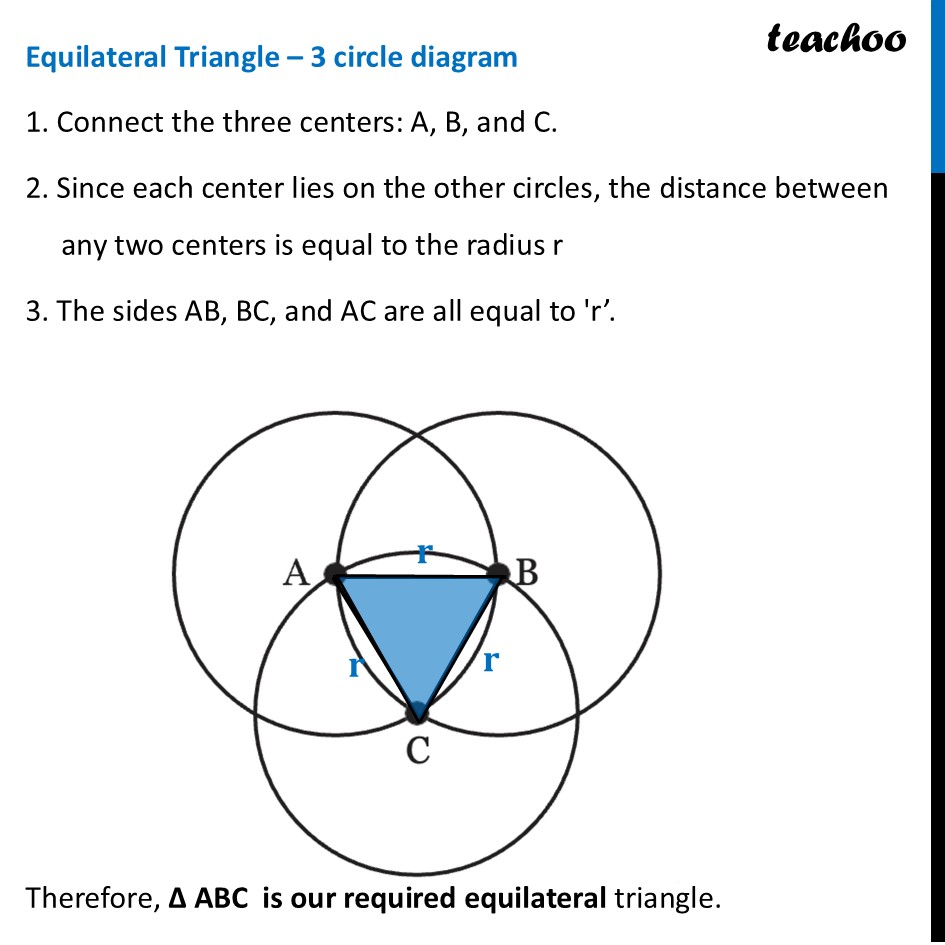
Question 2 Use the points on the circles and/or their centres to form isosceles and equilateral triangles. The circles are of the same size. We need to make both isosceles and equilateral triangle from these two diagrams Let’s make it Isosceles Triangle – 2 circle diagram 1. Mark intersection points as P & Q 2. Since P & Q lie on left circle – their distance from center (A) is radius i.e. AP = r & AQ = r 3. Join AP, AQ and PQ Thus, ∆ APQ is our required isosceles triangle Equilateral Triangle – 2 circle diagram 1. Since point B lies on left circle, it’s distance from center (A) is radius. Thus, AB = r. 2. Also, point P lies on left circle – it’s distance from center (A) is radius i.e. AP = r 3. And point P also lies on right circle - – it’s distance from center (A) is radius i.e. BP = r 4. Join AP, BP and AB Thus, ∆ APQ is our required isosceles triangle Isosceles Triangle – 3 circle diagram Many are possible. Let’s do one such way 1. Mark top intersection point P 2. Since P & C lie on left circle – their distance from center (A) is radius i.e. AP = r & AC = r 3. Join AP, AC and PC Thus, ∆ APC is our required isosceles triangle Equilateral Triangle – 3 circle diagram 1. Connect the three centers: A, B, and C. 2. Since each center lies on the other circles, the distance between any two centers is equal to the radius r 3. The sides AB, BC, and AC are all equal to 'r’. Therefore, ∆ ABC is our required equilateral triangle.