



Last updated at Dec. 16, 2024 by Teachoo





Transcript
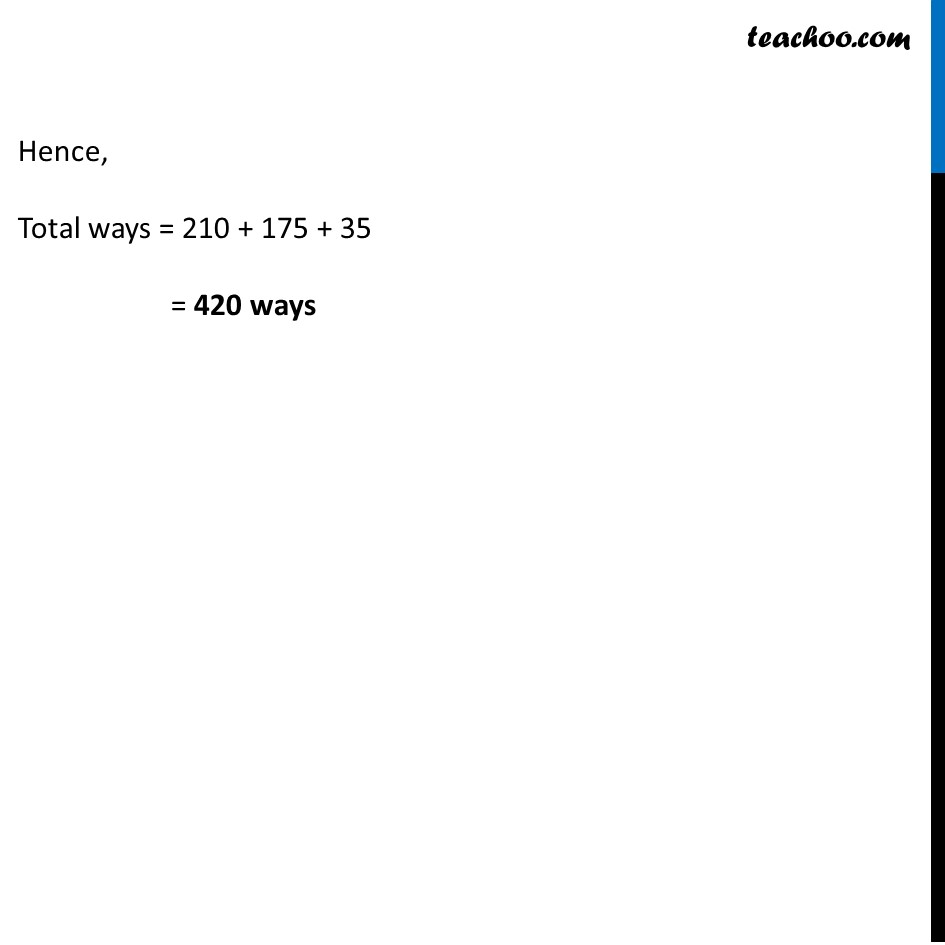
Misc 7 In an examination, a question paper consists of 12 questions divided into two parts i.e., Part I and Part II, containing 5 and 7 questions, respectively. A student is required to attempt 8 questions in all, selecting at least 3 from each part. In how many ways can a student select the questions? Student is required to attempt total 8 questions & selecting atleast 3 question from part 1 & part 2 Atleast means minimum So, she can select Option 1 3 from Part 1 & 5 from Part 2 Option 2 4 from Part 1 & 4 from Part 2 Option 3 5 from Part 1 & 3 from Part 2 We have to calculate all these combinations separately and then add it Option 1 – 3 questions from Part 1 and 5 Questions from Part 2 Number of ways selecting = 5C3 × 7C5 = 5!/3!(5 − 3)! × 7!/5!(7 − 5)! = 5!/(3! 2!) × 7!/(5! 2!) = (5 × 4 × 3!)/(3! 2!) × (7 × 6 × 5!)/(5! 2!) = 5 × 2 × 7 × 3 = 210 Option 2 – 4 questions from Part 1 and 4 Questions from Part 2 Number of ways selecting = 5C4 × 7C4 = 5!/4!(5 − 4)! × 7!/4!(7 − 4)! = 5!/(4! 1!) × 7!/(4! 3!) = (5 × 4!)/4! × (7 × 6 × 5 × 4!)/(4! 3!) = 5 × 7 × 5 = 175 Option 3 – 5 questions from Part 1 and 3 Questions from Part 2 Number of ways selecting = 5C5 × 7C3 = 5!/5!(5 − 5)! × 7!/3!(7 − 3)! = 5!/(5! 0!) × 7!/(3! 4!) = 5!/5! × (7 × 6 × 5 × 4!)/(3! 4!) = 1 × 7 × 5 = 35 Hence, Total ways = 210 + 175 + 35 = 420 ways