Ex 3.1, 6 - Chapter 3 Class 11 Trigonometric Functions

Transcript

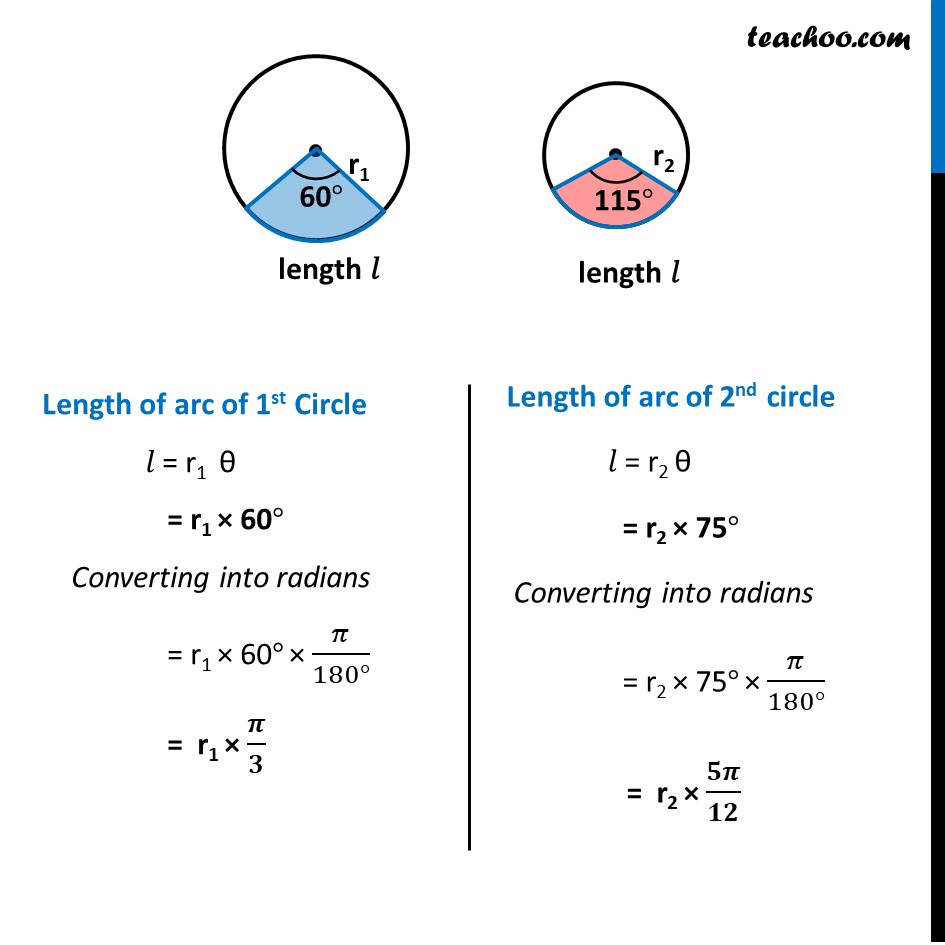
Ex 3.1, 6 If in two circles, arcs of the same length subtend angles 60° and 75° at the centre, find the ratio of their radii. We know that l = r θ There are 2 circle of different radius So, the radius be denoted by r1 and r2 Length of arc of Ist circle l = r1 θ = r1 × 60° = r1 × 60 × 𝜋/180 = r1 𝜋/3 It is given that arcs are of same length Hence Length of lst arc = length of llnd arc r1 × 𝜋/3 = r2 × 5𝜋/12 r1/𝑟2 = 5𝜋/12 × 3/𝜋 r1/r2 = 5/4 Hence r1 : r2 = 5 : 4 So, Ratio of radius = 5 : 4