Question 6 - Miscellaneous - Chapter 1 Class 11 Sets

Transcript

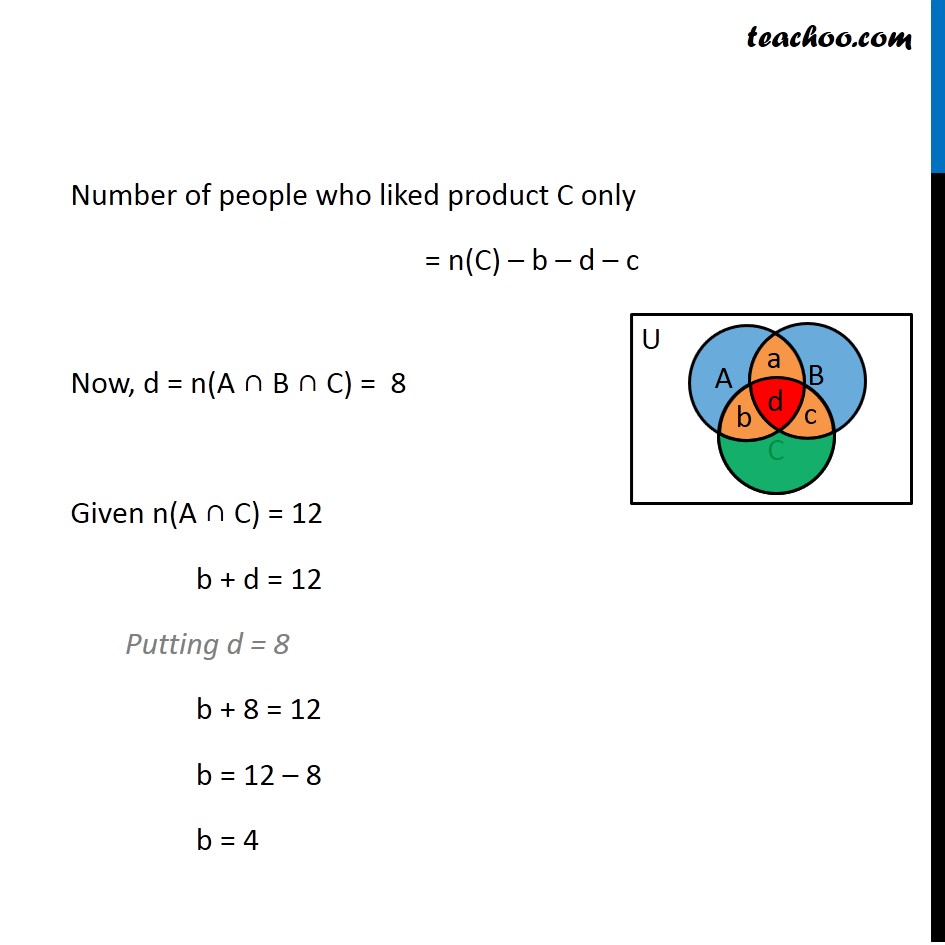
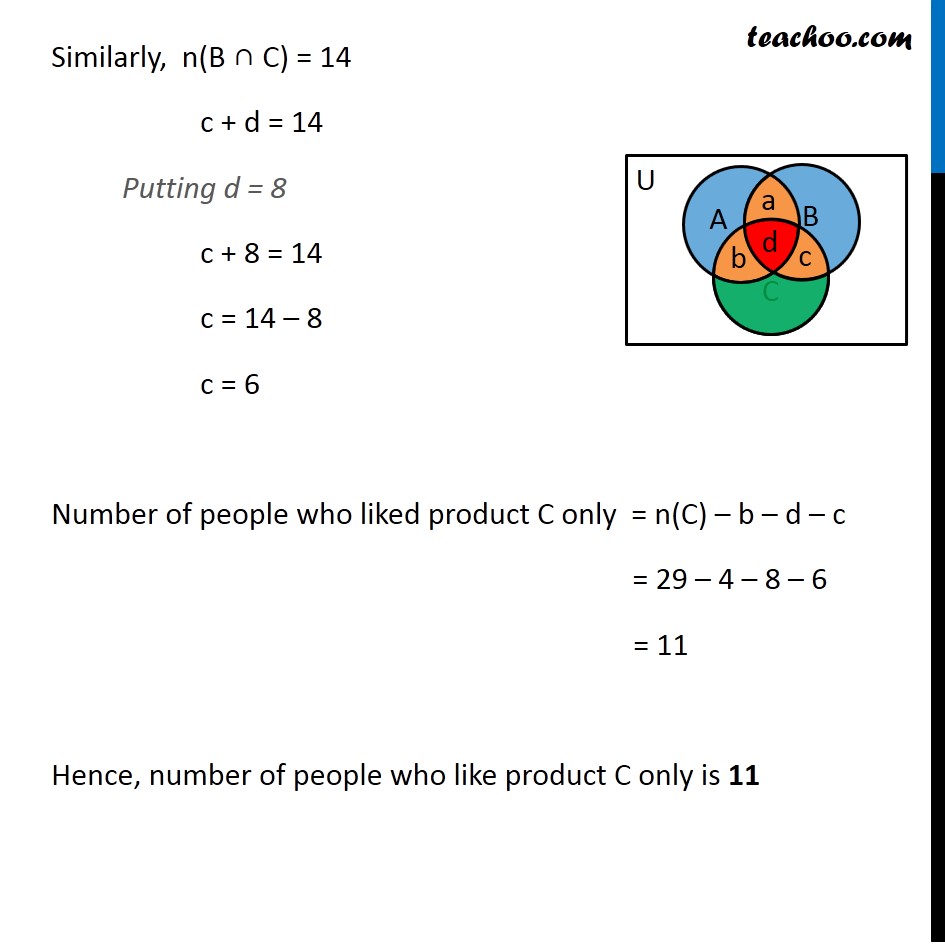
Question 6 In a survey it was found that 21 people liked product A, 26 liked product B & 29 liked product C. If 14 people liked products A & B, 12 people liked products C & A, 14 people liked products B & C and 8 liked all the three products. Find how many liked product C only. Let A, B, C be the set of people who like product A, product B & product C respectively Number of people who liked product A = n(A)= 21, Number of people who liked product B = n(B)= 26, Number of people who liked product C = n(C) = 29, Number of people who liked product A and B = n(A ∩ B) = 14, Number of people who liked product C and A = n(C ∩ A) = 12, Number of people who liked product B and C = n(B ∩ C) = 14, Number of people who liked all three products A ,B and C = n(A ∩ B ∩ C) = 8 We have to find how many people liked product C only. Let us draw a Venn diagram Let a denote number of people who liked product A & B but not C. Let b denote number of people who liked product A & C but not B. Let c denote number of people who liked product B & C but not A. Let d denote the number of people who liked all three products. Number of people who liked product C only = n(C) – b – d – c Now, d = n(A ∩ B ∩ C) = 8 Given n(A ∩ C) = 12 b + d = 12 Putting d = 8 b + 8 = 12 b = 12 – 8 b = 4 Similarly, n(B ∩ C) = 14 c + d = 14 Putting d = 8 c + 8 = 14 c = 14 – 8 c = 6 Number of people who liked product C only = n(C) – b – d – c = 29 – 4 – 8 – 6 = 11 Hence, number of people who like product C only is 11