Ex 13.2, 7 - Chapter 13 Class 10 Surface Areas and Volumes
Last updated at May 29, 2018 by Teachoo
Transcript
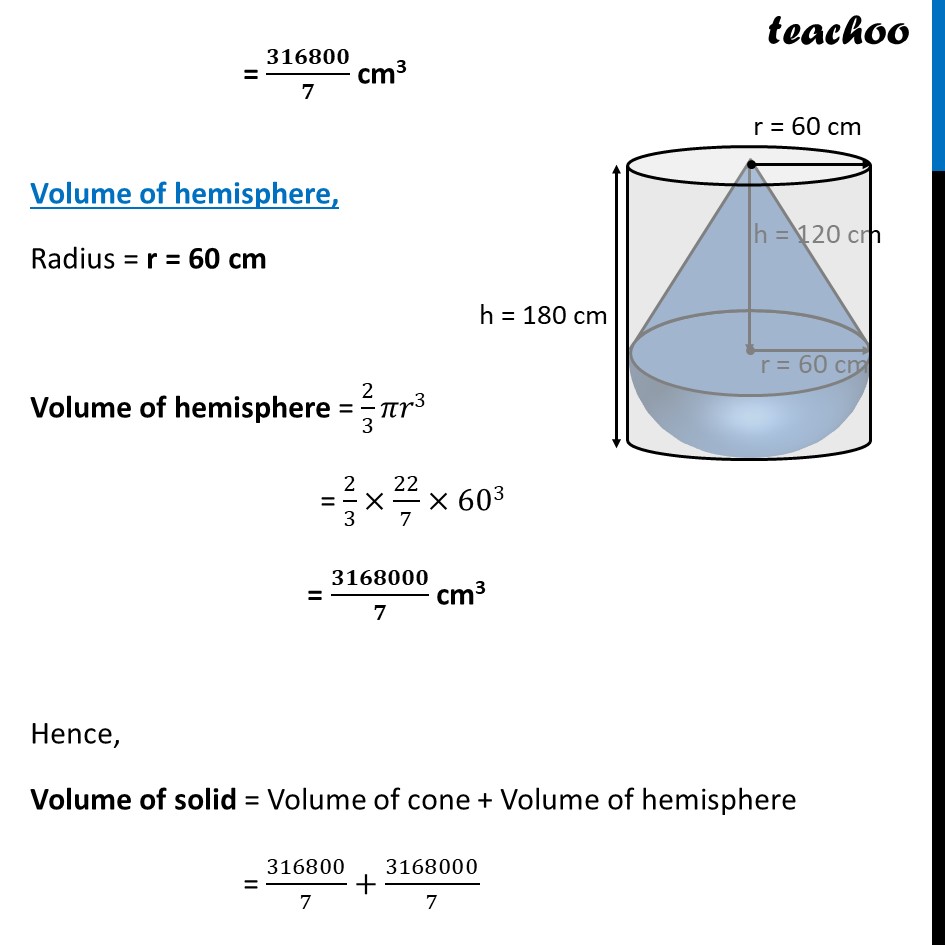
Ex 13.2, 7 A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm. Volume of water left in cylinder = Volume of cylinder Volume of solid Volume of cylinder Radius = r = 60 cm Height = h = 180 cm Volume of outer cylinder = 2 = 22/7 (60)2 180 = 14256000/7 Volume of solid Volume of solid = Volume of cone + volume of hemisphere Volume of cone Radius = r = 60 cm Height = h = 120 cm Volume of cone = 1/3 2 = 1/3 22/7 (60)2 12 = 316800/7 cm3 Volume of hemisphere, Radius = r = 60 cm Volume of hemisphere = 2/3 3 = 2/3 22/7 603 = 3168000/7 cm3 Hence, Volume of solid = Volume of cone + Volume of hemisphere = 316800/7+3168000/7 = 6336000/7 cm3 Now, Volume of water left in cylinder = Volume of cylinder Volume of solid = 14256000/7 6336000/7 = (14256000 6336000)/7 = (7920000/7) cm3 = 1131428.57 cm3 = 1131428.57 (1/100 m)^3 = 1131428.57 1/100 1/100 1/100 m3 = 1.131 m3 (approximately)
About the Author
Davneet Singh
Davneet Singh is a graduate from Indian Institute of Technology, Kanpur. He has been teaching from the past 8 years. He provides courses for Maths and Science at Teachoo. You can check his NCERT Solutions from Class 6 to 12.
sir please see that. In the formula of finding the volume of cone there is height of cone 120cm but while applying formula you changed this value to 12cm..... Why? Please answer...