Ex 9.1, 14 - Chapter 9 Class 10 Some Applications of Trignometry (Important Question)

Transcript

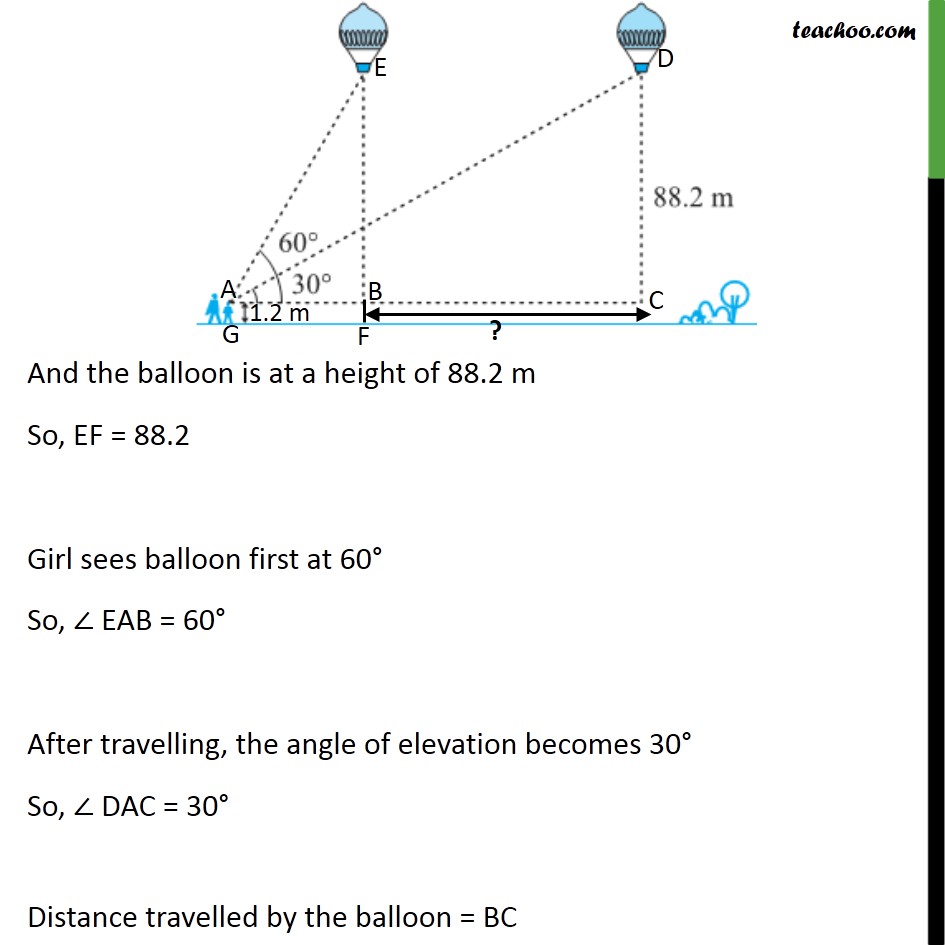
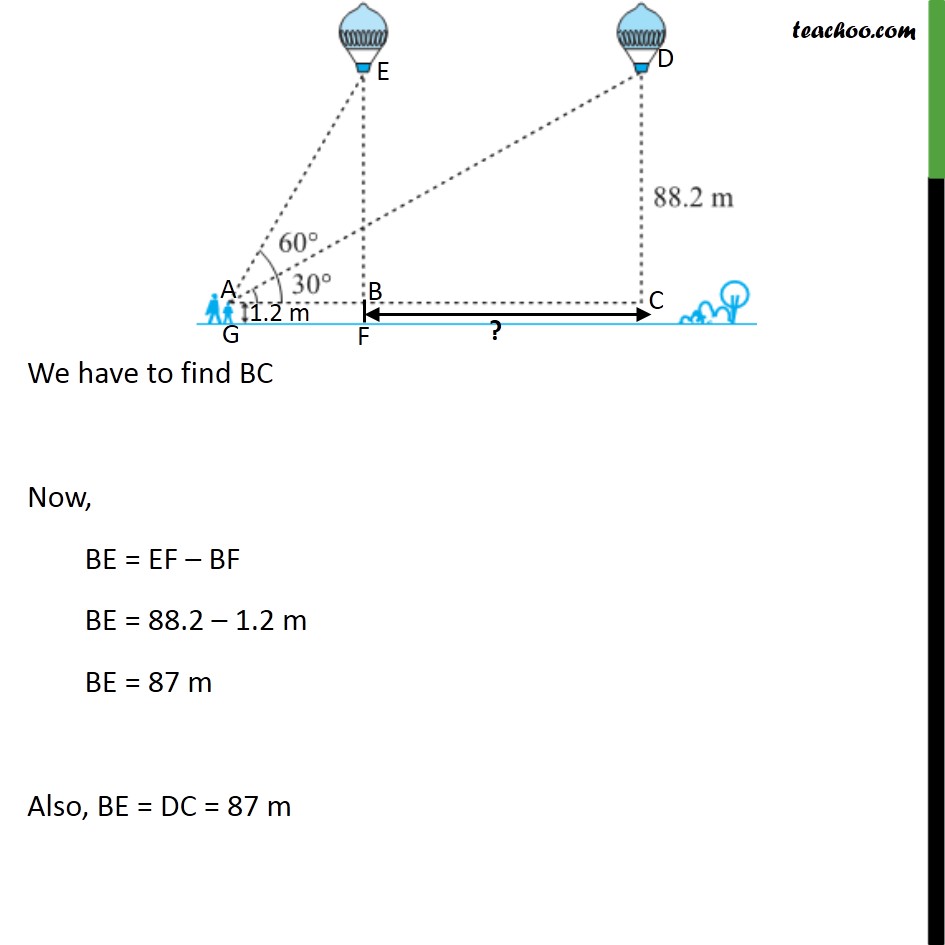
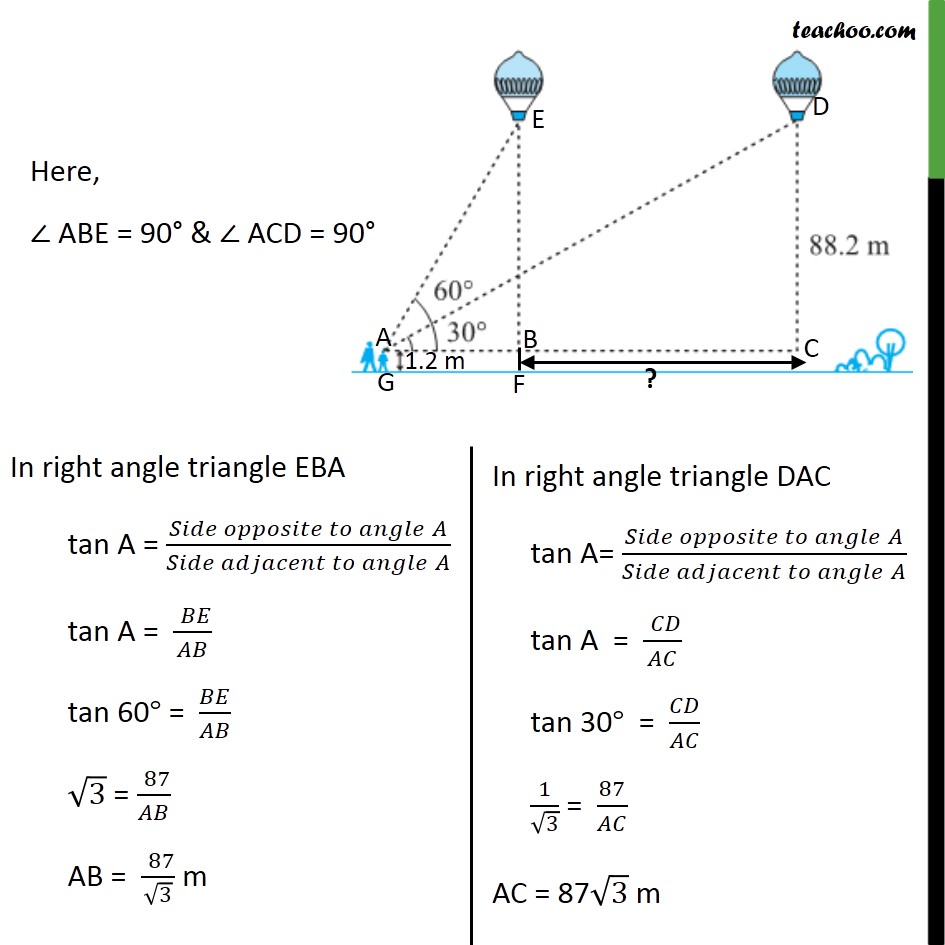
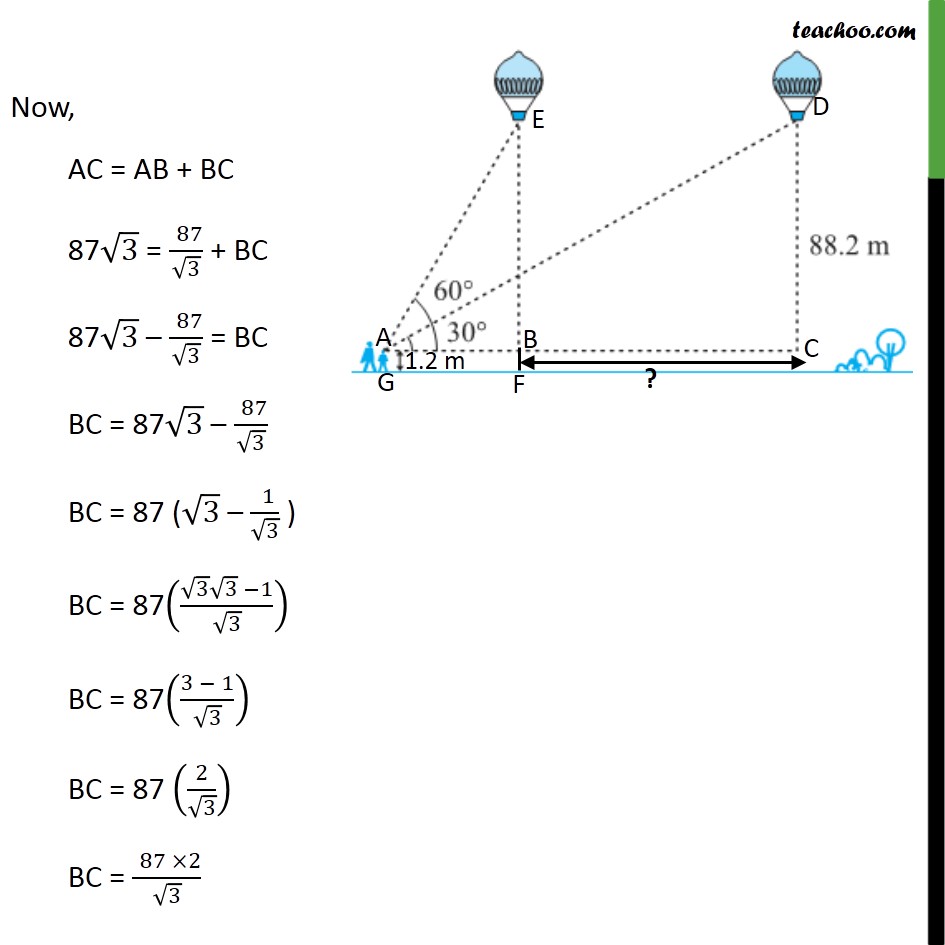
Ex 9.1 , 14 A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30° (see figure ). Find the distance travelled by the balloon during the interval. Given that 1.2 m tall girl sees a balloon So, AG = 1.2 m Also, AG & BF are parallel BF = AG = 1.2 m And the balloon is at a height of 88.2 m So, EF = 88.2 Girl sees balloon first at 60° So, ∠ EAB = 60° After travelling, the angle of elevation becomes 30° So, ∠ DAC = 30° Distance travelled by the balloon = BC We have to find BC Now, BE = EF – BF BE = 88.2 – 1.2 m BE = 87 m Also, BE = DC = 87 m Here, ∠ ABE = 90° & ∠ ACD = 90° Now, AC = AB + BC 87√3 = (" " 87)/√3 + BC 87√3 – (" " 87)/√3 = BC BC = 87√3 – (" " 87)/√3 BC = 87 (√3 – (" " 1)/√3 ) BC = 87((√3 √3 −1)/√3) BC = 87((3 − 1)/√3) BC = 87 (2/√3) BC = (" " 87 ×2)/√3 Multiply √3 in numerator and denominator BC = (" " 87 × 2)/√3 × √3/√3 BC = (" " 87 × 2 ×√3)/3 BC = 29×2×√3 BC = 58√3 Hence, distance travelled by balloon = 58√3 m