Ex 8.1, 10 - Chapter 8 Class 10 Introduction to Trignometry (Important Question)

Transcript

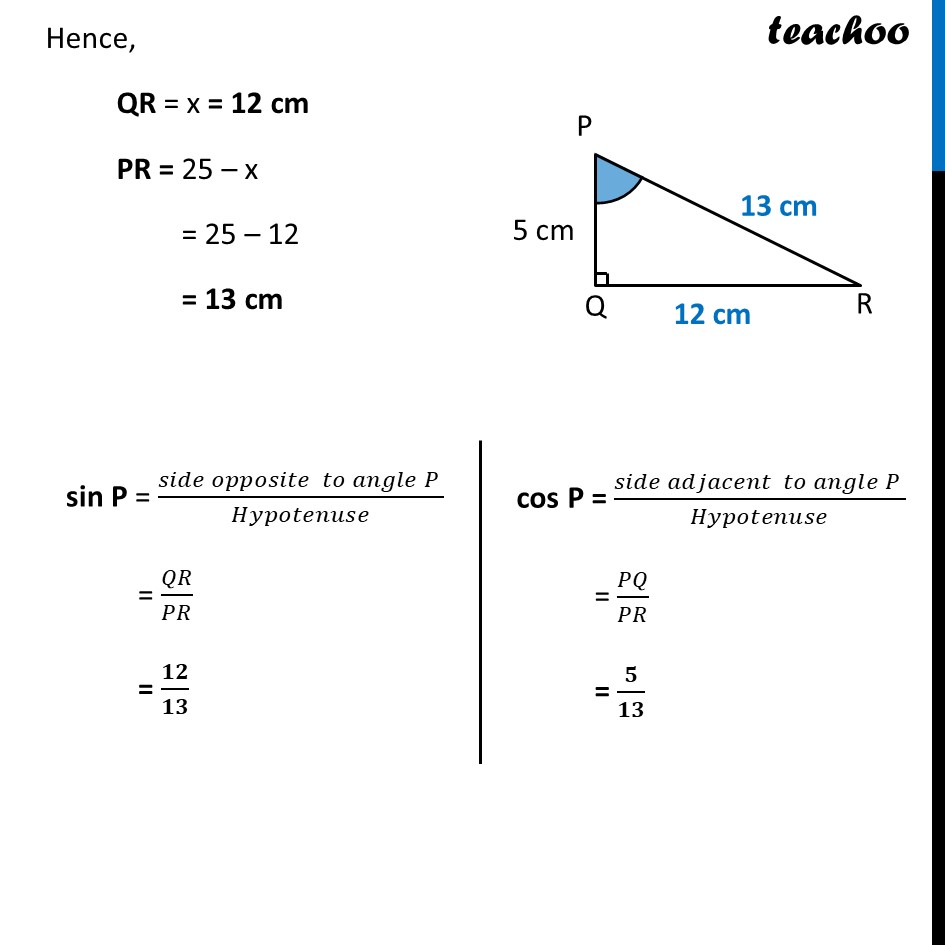
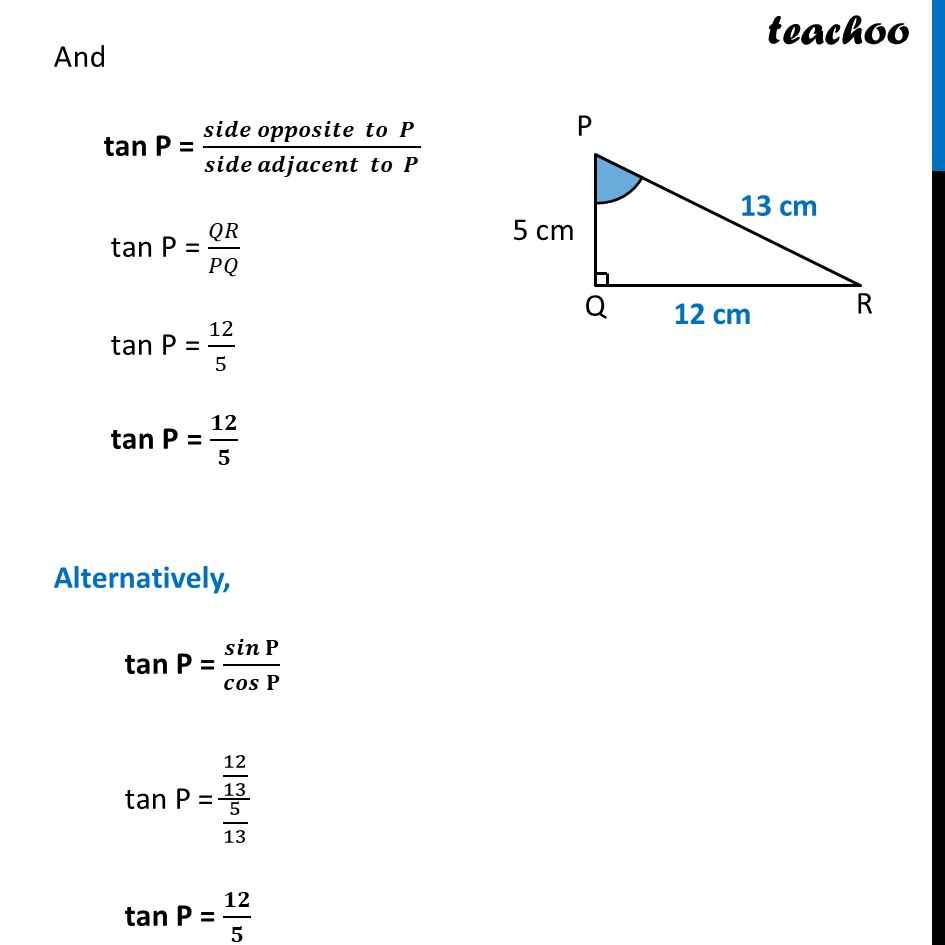
Ex 8.1, 10 In Δ PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P and tan P. Given PR + QR = 25 cm Let QR = x Thus, PR + QR = 25 cm PR = 25 – QR PR = 25 – x In right triangle PQR, Using Pythagoras theorem (Hypotenuse)2 = (Height)2 + (Base)2 PR2 = PQ2 + QR2 (25 – x)2 = 52 + x2 (25)2 + 𝑥2 − 2 × 25 × 𝑥=25+𝑥2 625 + x2 – 50x = 25 + x2 625 + x2 – 50x – 25 – x2 = 0 x2 – x2 – 50x + 625 – 25 = 0 − 50𝑥 + 600 = 0 − 50𝑥 = −600 x = (− 600)/(− 50) x = 12 Hence, QR = x = 12 cm PR = 25 – x = 25 – 12 = 13 cm sin P = (𝑠𝑖𝑑𝑒 𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒 𝑃 )/𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒 = 𝑄𝑅/𝑃𝑅 = 𝟏𝟐/𝟏𝟑 cos P = (𝑠𝑖𝑑𝑒 𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡 𝑡𝑜 𝑎𝑛𝑔𝑙𝑒 𝑃 )/𝐻𝑦𝑝𝑜𝑡𝑒𝑛𝑢𝑠𝑒 = 𝑃𝑄/𝑃𝑅 = 𝟓/𝟏𝟑 And tan P = (𝒔𝒊𝒅𝒆 𝒐𝒑𝒑𝒐𝒔𝒊𝒕𝒆 𝒕𝒐 𝑷 )/(𝒔𝒊𝒅𝒆 𝒂𝒅𝒋𝒂𝒄𝒆𝒏𝒕 𝒕𝒐 𝑷) tan P = 𝑄𝑅/𝑃𝑄 tan P = 12/5 tan P = 𝟏𝟐/𝟓 Alternatively, tan P = 𝒔𝒊𝒏⁡𝐏/𝒄𝒐𝒔⁡𝐏 tan P = (12/13)/(5/13) tan P = 𝟏𝟐/𝟓