Ex 6.2, 7 - Chapter 6 Class 10 Triangles

Transcript

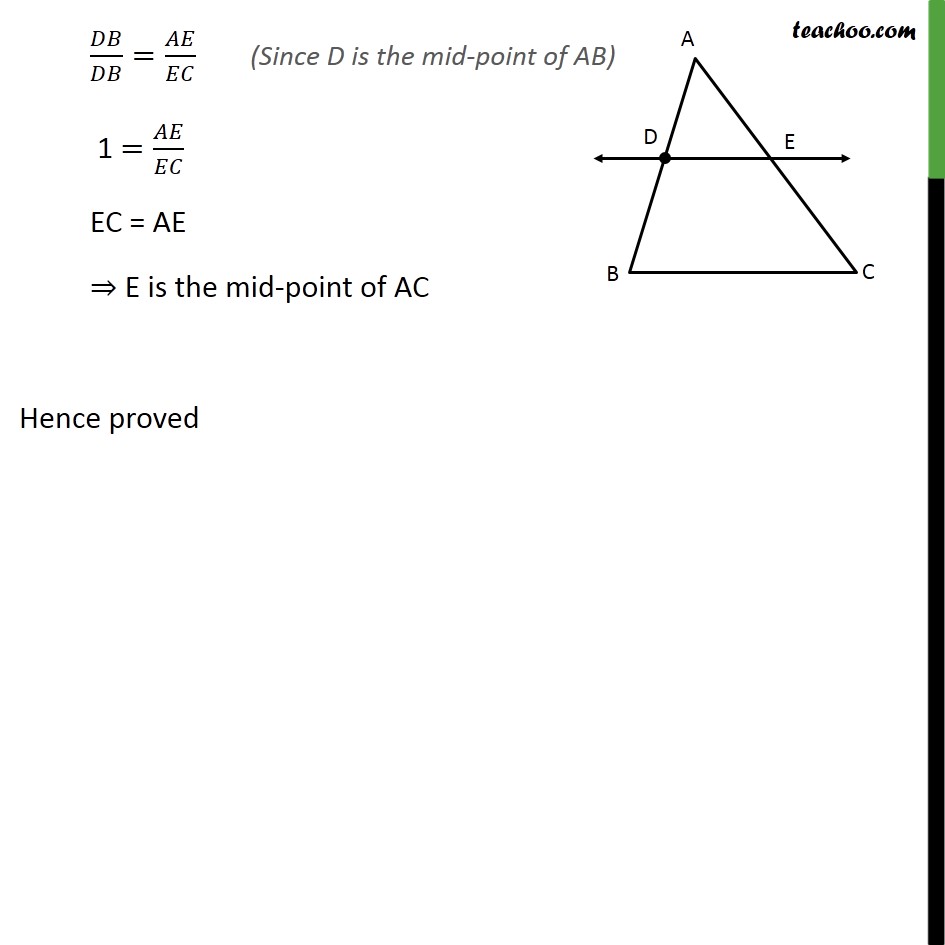
Ex 6.2, 7 Using Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX). Given: Let us assume ABC Where DE is parallel to BC & D is the mid point of AB To prove: E is the mid point of AC Proof: In ABC , DE II BC We know that if a line drawn parallel to one side of triangle, intersects the other two sides in distinct points, then it divides the other 2 side in same ratio / = / / = / 1 = / EC = AE E is the mid-point of AC Hence proved