Ex 1.4, 3 - Chapter 1 Class 10 Real Numbers

Transcript

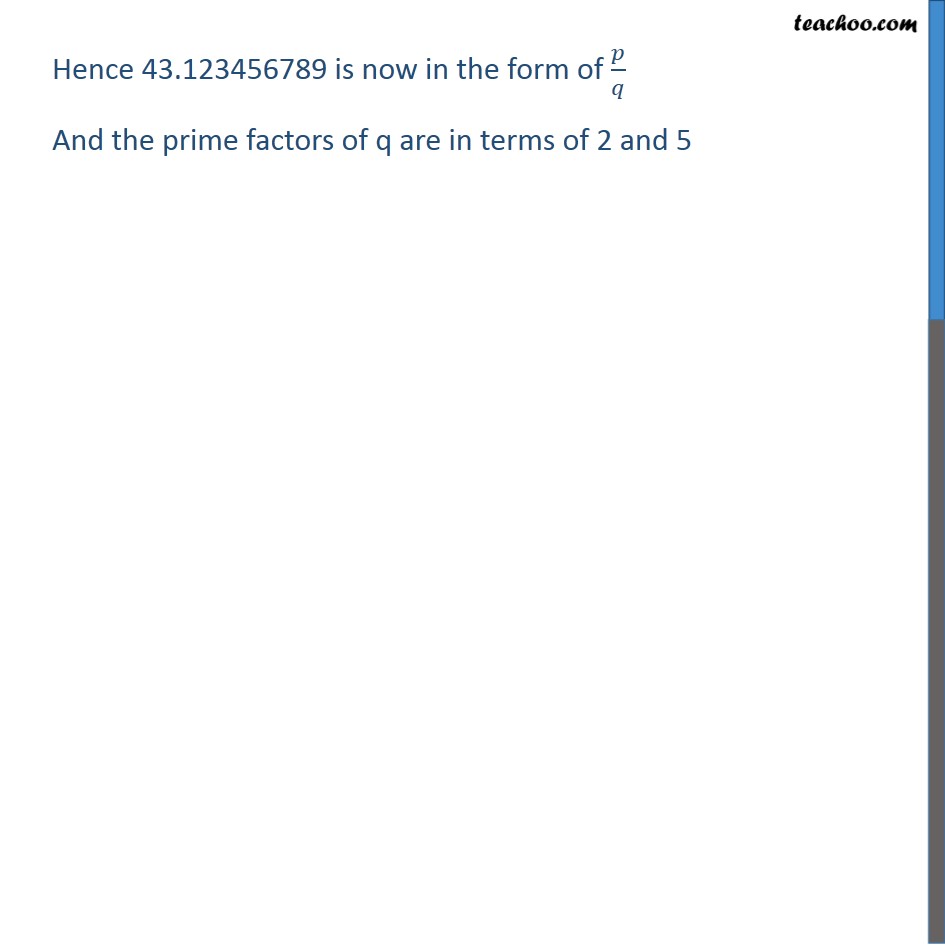
Ex 1.4 , 3 (Method 1) The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form , 𝑝/𝑞 what can you say about the prime factors of q? 43.123456789 43.123456789 is terminating So, it would be a rational number 43.123456789 = 43123456789/1000000000 = 43123456789/(10)9 = 43123456789/(2 ×5)9 = 43123456789/(29 ×59) Hence 43.123456789 is now in the form of 𝑝/𝑞 And the prime factors of q are in terms of 2 and 5 Ex 1.4 , 3 (Method 2) The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form , 𝑝/𝑞 what can you say about the prime factors of q? 43.123456789 43.123456789 is terminating So, it would be a rational number In a terminating expansion of 𝑝/𝑞, q is of the form 2n 5m So, prime factors of q will be 2 or 5 or both only. Ex 1.4 , 3 The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form , 𝑝/𝑞 what can you say about the prime factors of q? (ii) 0.120120012000120000… 0.120120012000120000… is non terminating and non repeating So, it is not a rational number Ex 1.4 , 3 The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form , 𝑝/𝑞 what can you say about the prime factors of q? (iii) 43. ("123456789" ) ̅ Here 43. ("123456789" ) ̅ is non terminating but repeating. So, it would be a rational number In a non- terminating , repeating expansion of 𝑝/𝑞, q will have factors other than 2 or 5.