You are here
Square Formulas
- (a + b) 2 = a 2 + b 2 + 2ab
- (a − b) 2 = a 2 + b 2 − 2ab
- a 2 − b 2 = (a − b) (a + b)
- (x + a) (x + b) = x 2 + (a + b) x + ab
- (a + b + c) 2 = a 2 + b 2 + c 2 + 2ab + 2bc + 2ca
-
(a + (−b) + (−c))
2
= a
2
+ (−b)
2
+ (−c)
2
+ 2a (−b) + 2 (−b) (−c) + 2a (−c)
(a – b – c) 2 = a 2 + b 2 + c 2 − 2ab + 2bc − 2ca
Cube Formulas
- (a + b) 3 = a 3 + b 3 + 3ab(a + b)
- (a − b) 3 = a 3 - b 3 - 3ab(a - b)
- a 3 − b 3 = (a − b) (a 2 + b 2 + ab)
- a 3 + b 3 = (a + b) (a 2 + b 2 − ab)
- (a + b + c) 3 = a 3 + b 3 + c 3 + 3(a + b)(b + c)(c + a)
- a 3 + b 3 + c 3 − 3abc = (a + b + c) (a 2 + b 2 + c 2 − ab − bc − ac)
-
If (a + b + c) = 0,
a 3 + b 3 + c 3 = 3abc
Some not so Common Formulas
Power n Formula
- a n − b n = (a − b) (a n−1 + a n−2 b 1 + a n−3 b 2 + .... + a 1 b n−2 + b n−1 )
Exponent Law
-
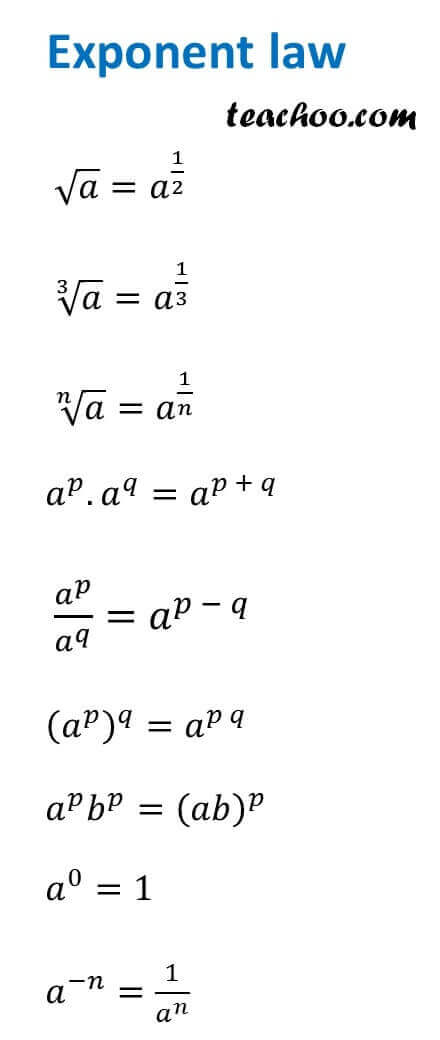
√a = a 1/2
-
∛a = a 1/3
-
n √a = a 1/n
- a p. a q = a p + q
- a p / a q = a p - q
- a p. b p = (ab) p
- (a p ) q. = a pq
- a 0 . = 1
- a –n. = 1/a n
For Irrational Numbers
Quadratic Formula
