Example 3 - Chapter 12 Class 9 Herons Formula (Important Question)

Transcript

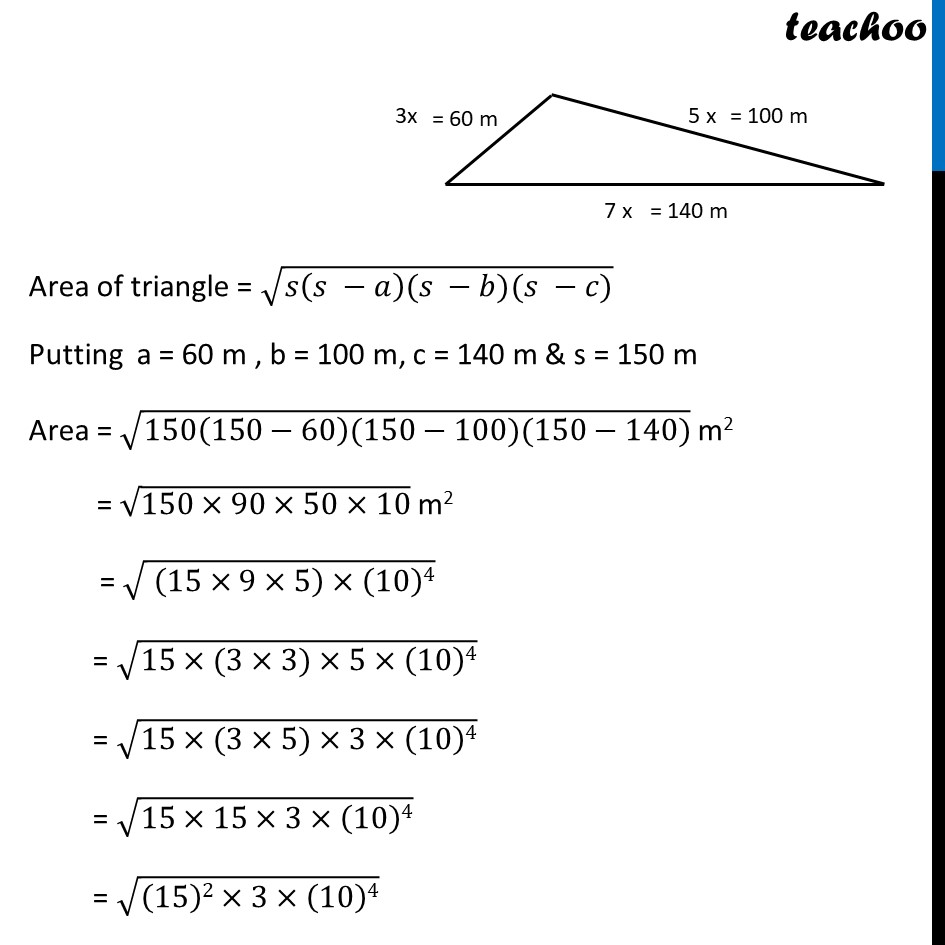
Example 3 The sides of a triangular plot are in the ratio of 3 : 5 : 7 and its perimeter is 300 m. Find its area. Area of triangle = √(s(s−a)(s−b)(s −c)) Here, s is the semi-perimeter, and a, b, c are the sides of the triangle Given Perimeter = 300 m Semi-Perimeter = s =Perimeter/2 s = 300/2 s = 150 m Given Ratio of sides is 3 : 5 : 7 Let sides be a = 3x meters , b = 5x meters , c = 7x meters where x is any number Now, Perimeter = 300 m a + b + c = 300 3x + 5x + 7x = 300 15x = 300 x = 300/15 x = 20 So, a = 3x meter b = 5x m c = 7x m Area of triangle = √(𝑠(𝑠 −𝑎)(𝑠 −𝑏)(𝑠 −𝑐)) Putting a = 60 m , b = 100 m, c = 140 m & s = 150 m Area = √(150(150−60)(150−100)(150−140)) m2 = √(150×90×50×10) m2 = √( (15×9×5)×(10)4) = √(15×(3×3)×5×(10)4) = √(15×(3×5)×3×(10)4) = √(15×15×3×(10)4) = √((15)2×3×(10)4) = √((15)2)×√3× √104 = (15) ×√3× 〖(104)〗^(1/2) = (15)×√3 × (102) = (15)×√3 × (100) = 1500√3 Thus, Area = 1500√3 m2