

Area of Quadrilateral using Heron's formula
Last updated at Dec. 13, 2024 by Teachoo





Transcript
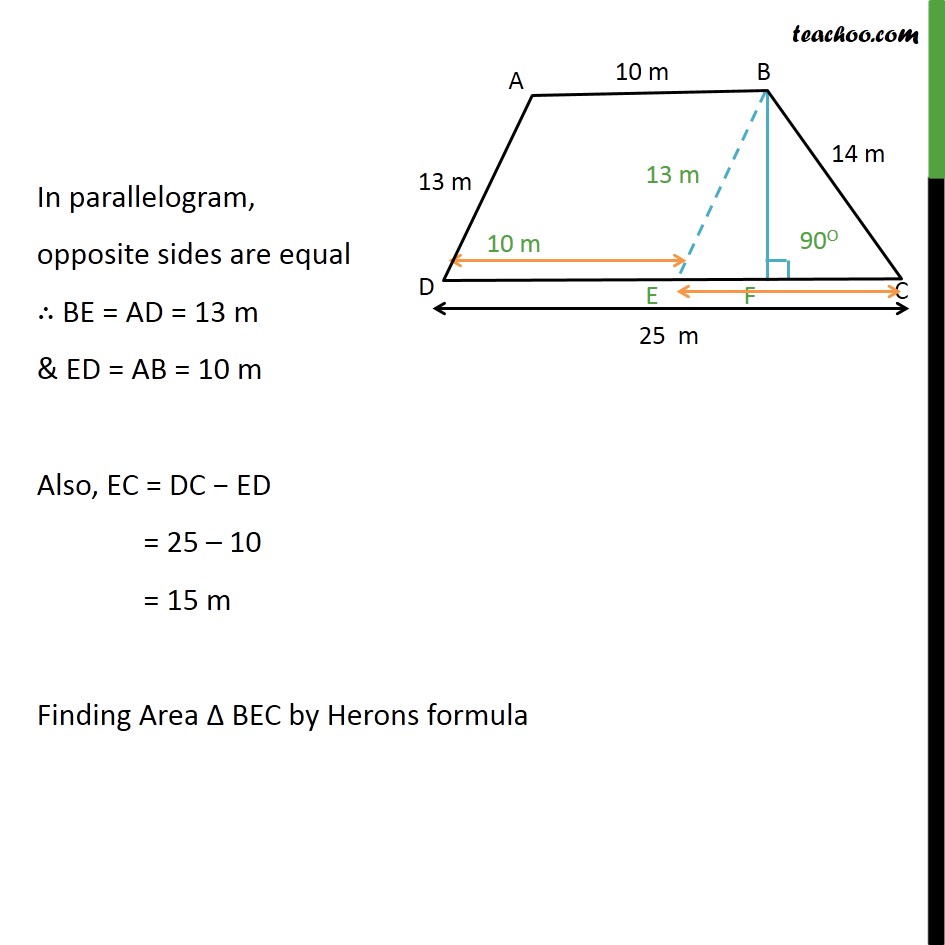
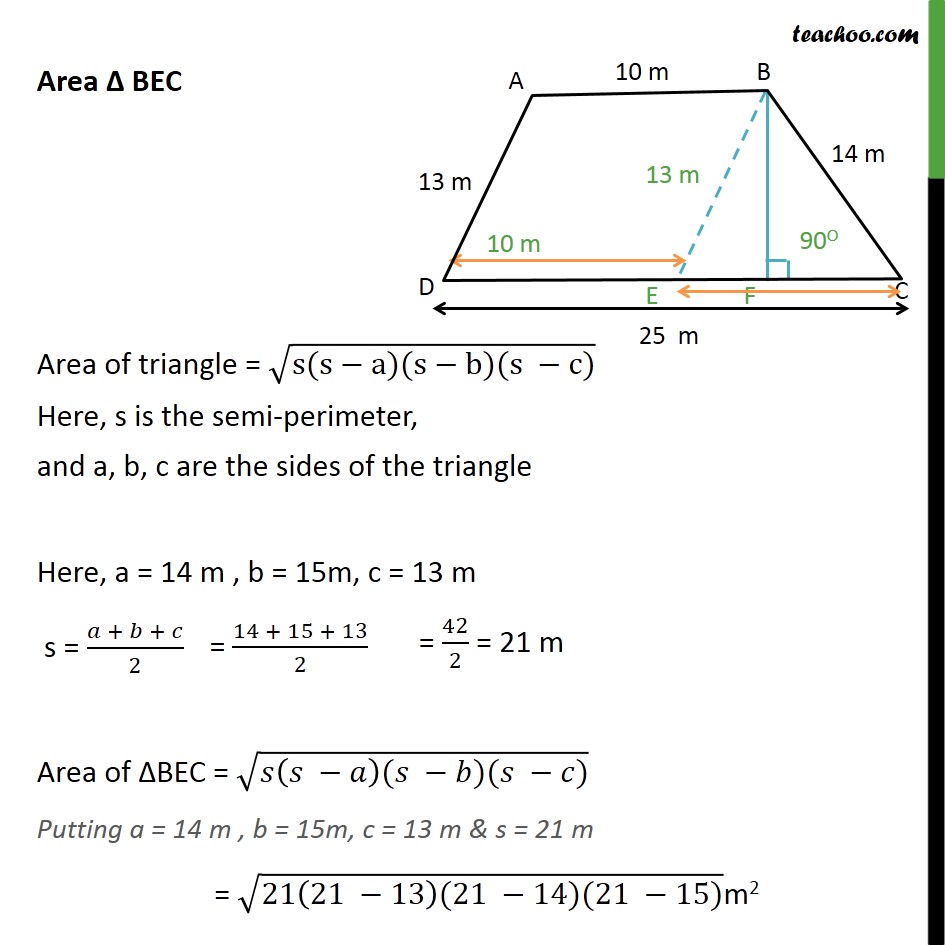
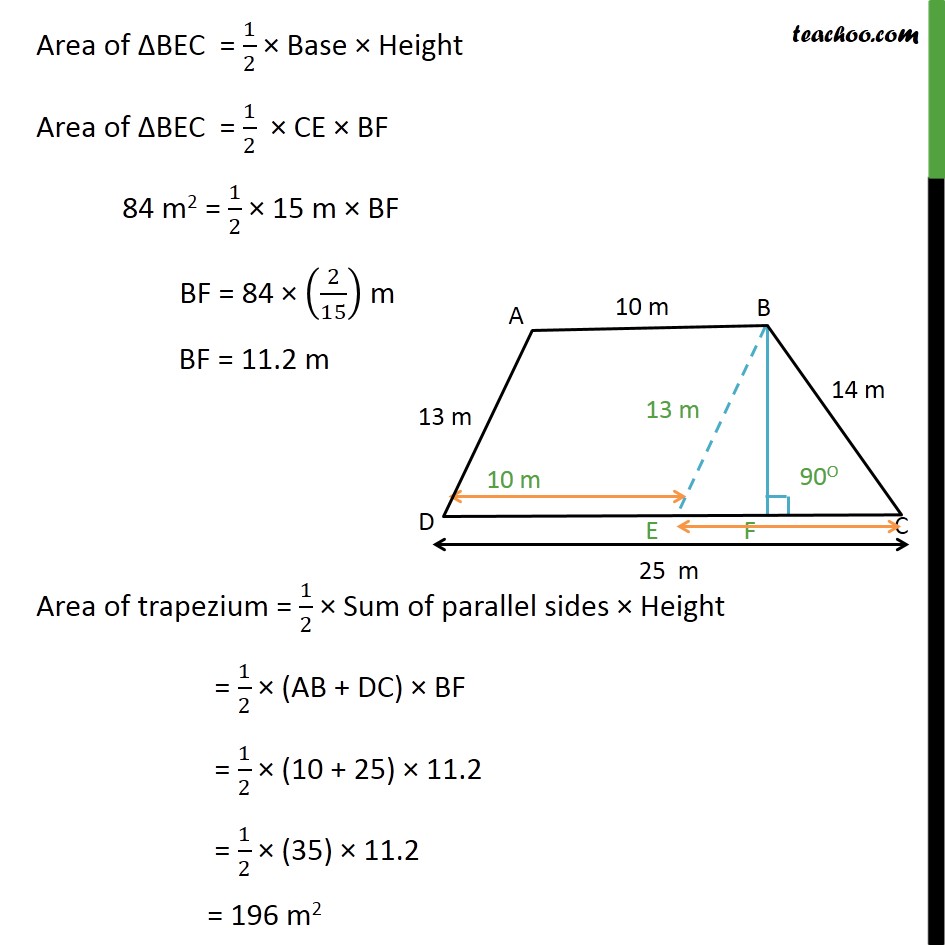
Question 9 A field is in the shape of a trapezium whose parallel sides are 25 m and 10 m. The non-parallel sides are 14 m and 13 m. Find the area of the field. Area of trapezium = 1/2 Sum of parallel sides Height = 1/2 (AB + DC) BF To calculate BF, we do the following steps Step 1: Draw BE AD Note AB DE Since, opposite sides are parallel, ABED is a parallelogram In parallelogram, opposite sides are equal BE = AD = 13 m & ED = AB = 10 m Also, EC = DC ED = 25 10 = 15 m Finding Area BEC by Herons formula Area BEC Area of triangle = (s(s a)(s b)(s c)) Here, s is the semi-perimeter, and a, b, c are the sides of the triangle Here, a = 14 m , b = 15m, c = 13 m s = ( + + )/2 Area of BEC = ( ( )( )( )) Putting a = 14 m , b = 15m, c = 13 m & s = 21 m = (21(21 13)(21 14)(21 15))m2 = (21(8)(7)(6)) = ((7 3) (8) (7) (2 3)) = ((7 7) (8 2) (3 3)) = ((7 7) (16) (3 3)) = ((72) (42) (32)) = ((7)2) ((4)2) ((3)2) = 7 4 3 = 84 m2 Since BEC has height BF and base EC, we use base height formula to find area Area of BEC = 1/2 Base Height Area of BEC = 1/2 CE BF 84 m2 = 1/2 15 m BF BF = 84 (2/15) m BF = 11.2 m Area of trapezium = 1/2 Sum of parallel sides Height = 1/2 (AB + DC) BF = 1/2 (10 + 25) 11.2 = 1/2 (35) 11.2 = 196 m2