
Area of Quadrilateral using Heron's formula
Last updated at Dec. 13, 2024 by Teachoo





Transcript
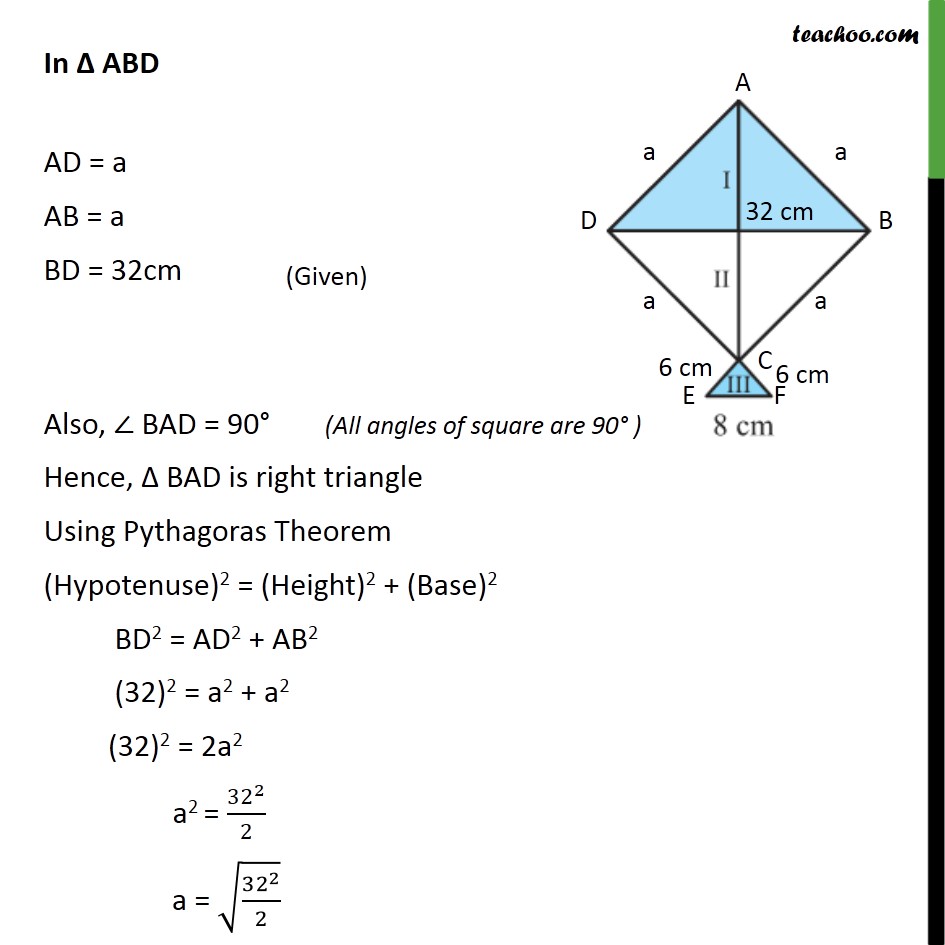
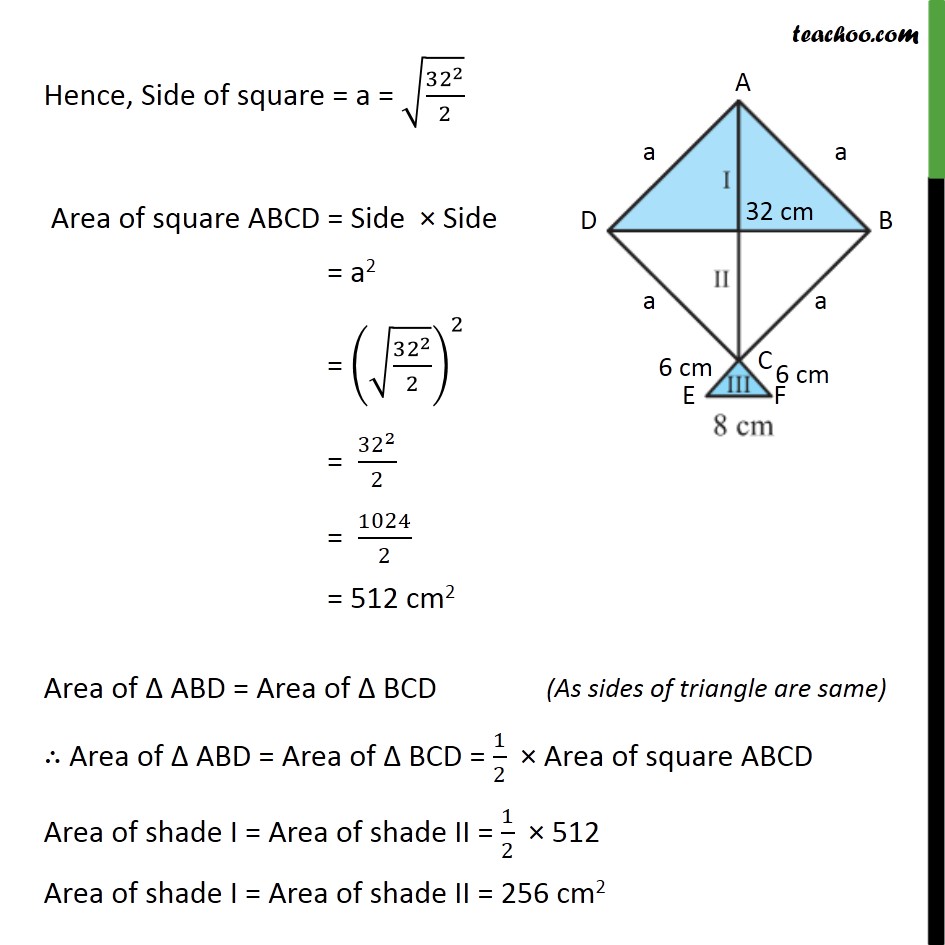
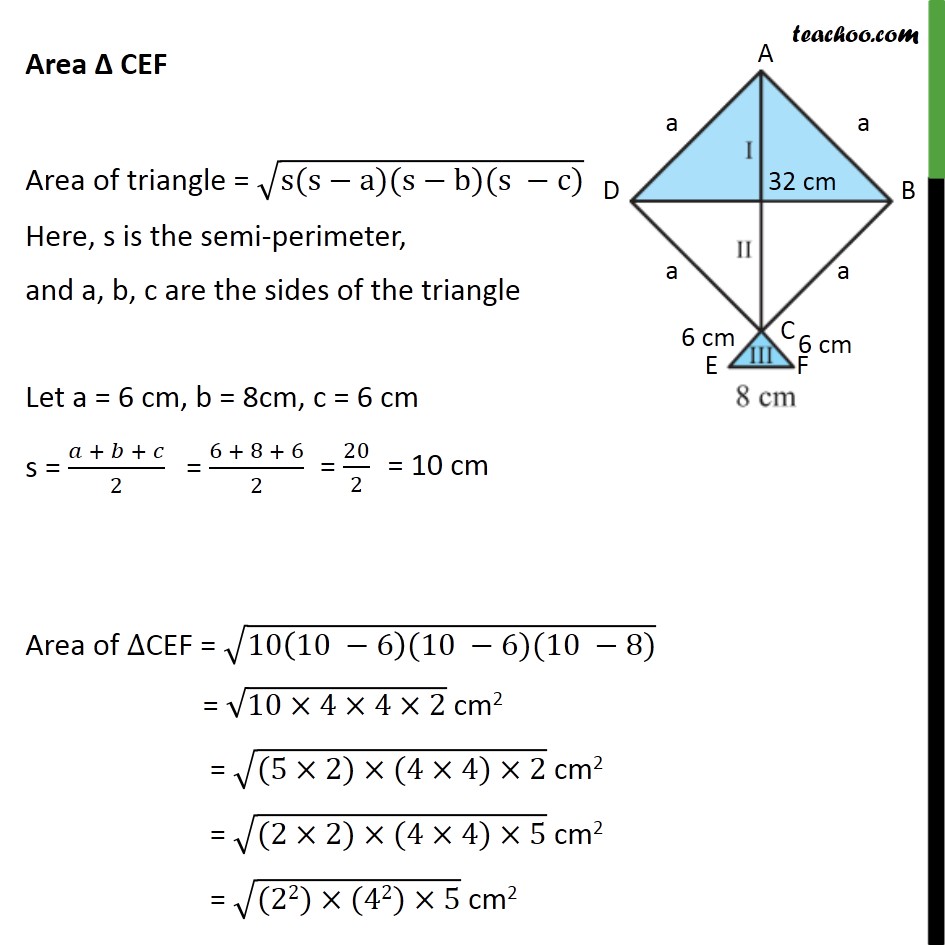
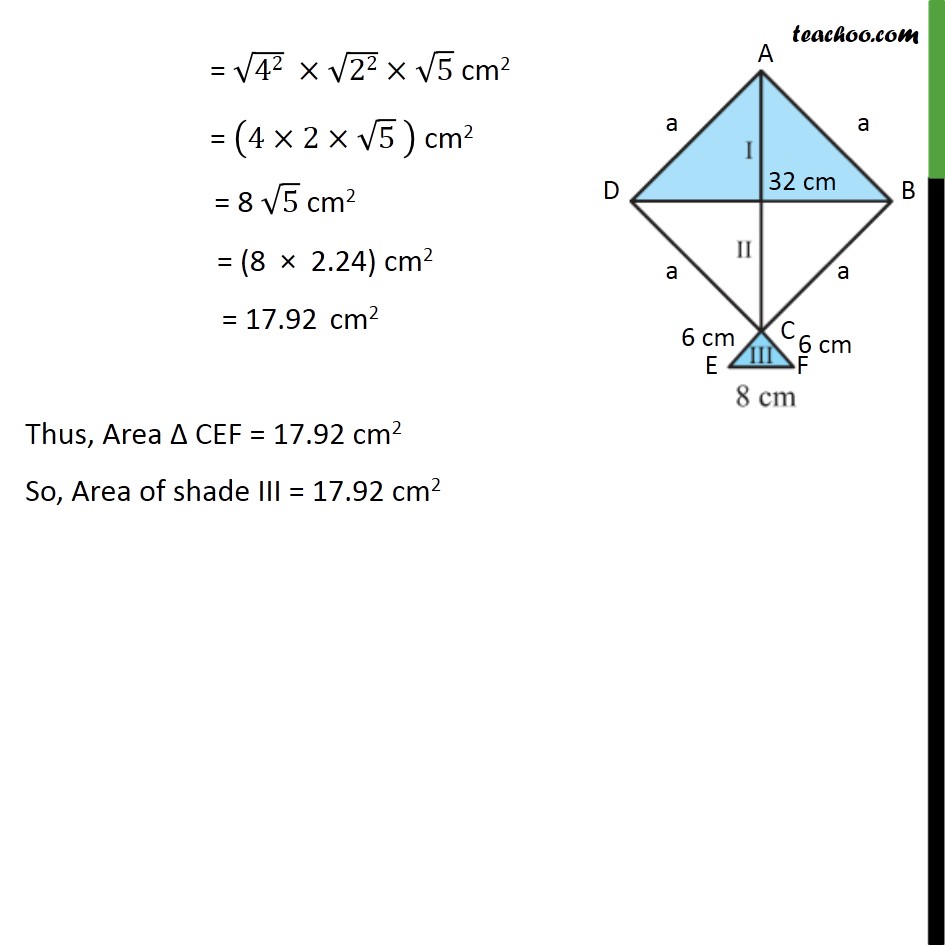
Question 7 A kite in the shape of a square with a diagonal 32 cm and an isosceles triangles of base 8 cm and sides 6 cm each is to be made of three different shades as shown in the given figure. How much paper of each shade has been used in it? Given ABCD is a square AB = BC = CD = DA Hence, AB = DB = CD = AD = a Now, there are 3 triangles, Δ ABD, Δ BCD, Δ DCE In Δ ABD AD = a AB = a BD = 32cm Also, ∠ BAD = 90° Hence, Δ BAD is right triangle Using Pythagoras Theorem (Hypotenuse)2 = (Height)2 + (Base)2 BD2 = AD2 + AB2 (32)2 = a2 + a2 (32)2 = 2a2 a2 = 〖32〗^2/2 a = √(〖32〗^2/2) Hence, Side of square = a = √(〖32〗^2/2) Area of square ABCD = Side × Side = a2 = (√(〖32〗^2/2))^2 = 〖32〗^2/2 = 1024/2 = 512 cm2 Area of Δ ABD = Area of Δ BCD ∴ Area of Δ ABD = Area of Δ BCD = 1/2 × Area of square ABCD Area of shade I = Area of shade II = 1/2 × 512 Area of shade I = Area of shade II = 256 cm2 Area Δ CEF Area of triangle = √(s(s−a)(s−b)(s −c)) Here, s is the semi-perimeter, and a, b, c are the sides of the triangle Let a = 6 cm, b = 8cm, c = 6 cm s = (𝑎 + 𝑏 + 𝑐)/2 Area of ∆CEF = √(10(10 −6)(10 −6)(10 −8)) = √(10×4×4×2) cm2 = √((5×2)×(4×4)×2) cm2 = √((2×2)×(4×4)×5) cm2 = √((22)×(42)×5) cm2 = √42 ×√22×√5 cm2 = (4×2×√5 " " ) cm2 = 8 √5 cm2 = (8 × 2.24) cm2 = 17.92 cm2 Thus, Area Δ CEF = 17.92 cm2 So, Area of shade III = 17.92 cm2