Check sibling questions

Question 4 - Area of Quadrilateral using Heron's formula - Chapter 10 Class 9 Herons Formula

Last updated at May 29, 2023 by

Ex 12.2, 4 - A triangle and a parallelogram have same base - Ex 12.2

Ex 12.2, 4 - Chapter 12 Class 9 Herons Formula - Part 2
Ex 12.2, 4 - Chapter 12 Class 9 Herons Formula - Part 3

Learn in your speed, with individual attention - Teachoo Maths 1-on-1 Class

Book a free demo

Transcript

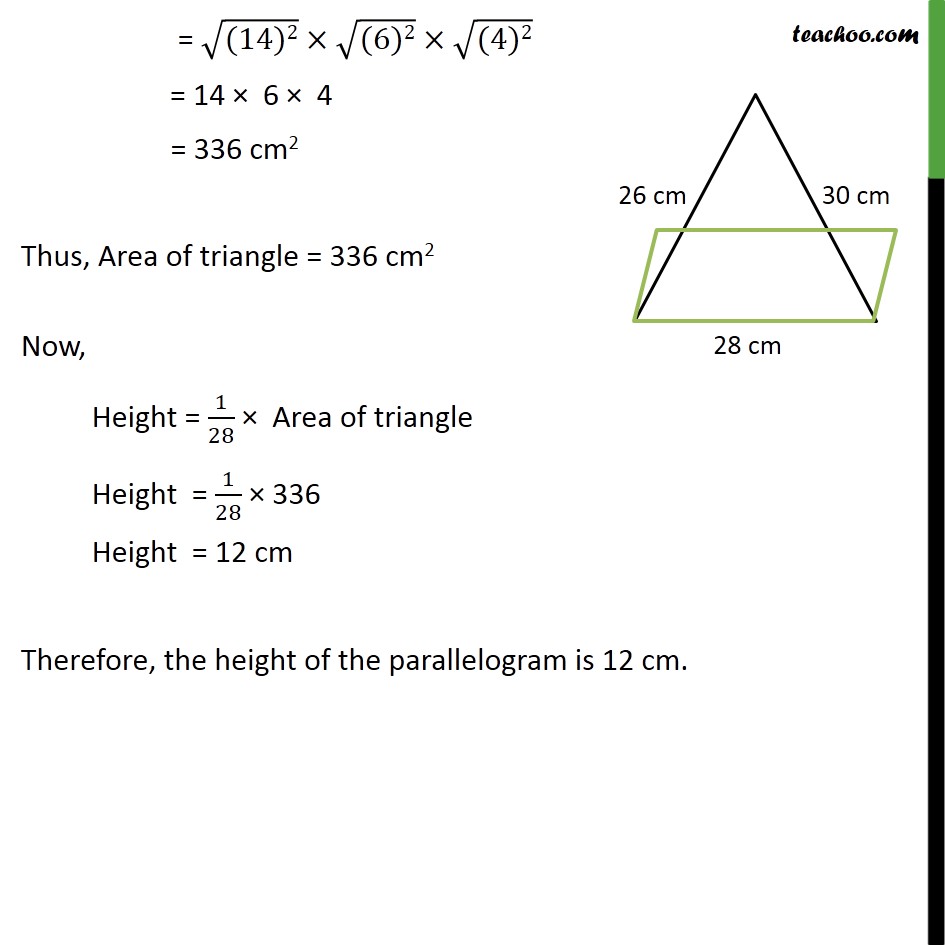
Question 4 A triangle and a parallelogram have the same base and the same area. If the sides of triangle are 26 cm, 28 cm and 30 cm, and the parallelogram stands on the base 28 cm, find the height of the parallelogram. Given that Area of parallelogram = Area of triangle Base Height = Area of triangle 28 Height = Area of triangle Height = 1/28 Area of triangle Finding Area of triangle Area of triangle Area of triangle = (s(s a)(s b)(s c)) Here, s is the semi-perimeter, and a, b, c are the sides of the triangle Here, a = 26 , b = 28 , c = 30 s = ( + + )/2 Area of triangle = (42(42 26)(42 28)(42 30)) cm2 = (42(16)(14)(12)) = ((14 3) (16) (14) (12)) = ((14 14) (12 3) (16) ) = ((142) (36) (16) ) = ((142) (62) (42) ) = ((14)2) ((6)2) ((4)2) = 14 6 4 = 336 cm2 Thus, Area of triangle = 336 cm2 Now, Height = 1/28 Area of triangle Height = 1/28 336 Height = 12 cm Therefore, the height of the parallelogram is 12 cm.

Ask a doubt
Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 13 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.