Ex 12.2, 2 - Chapter 12 Class 9 Herons Formula (Term 1)

Transcript

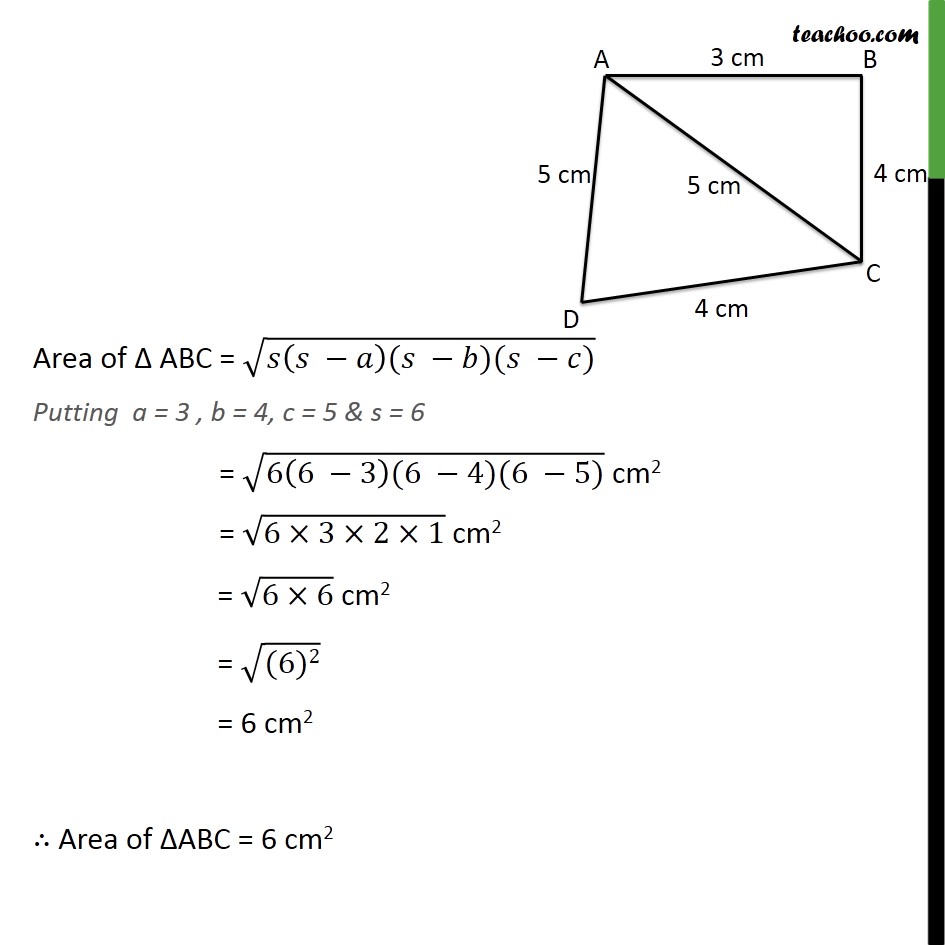
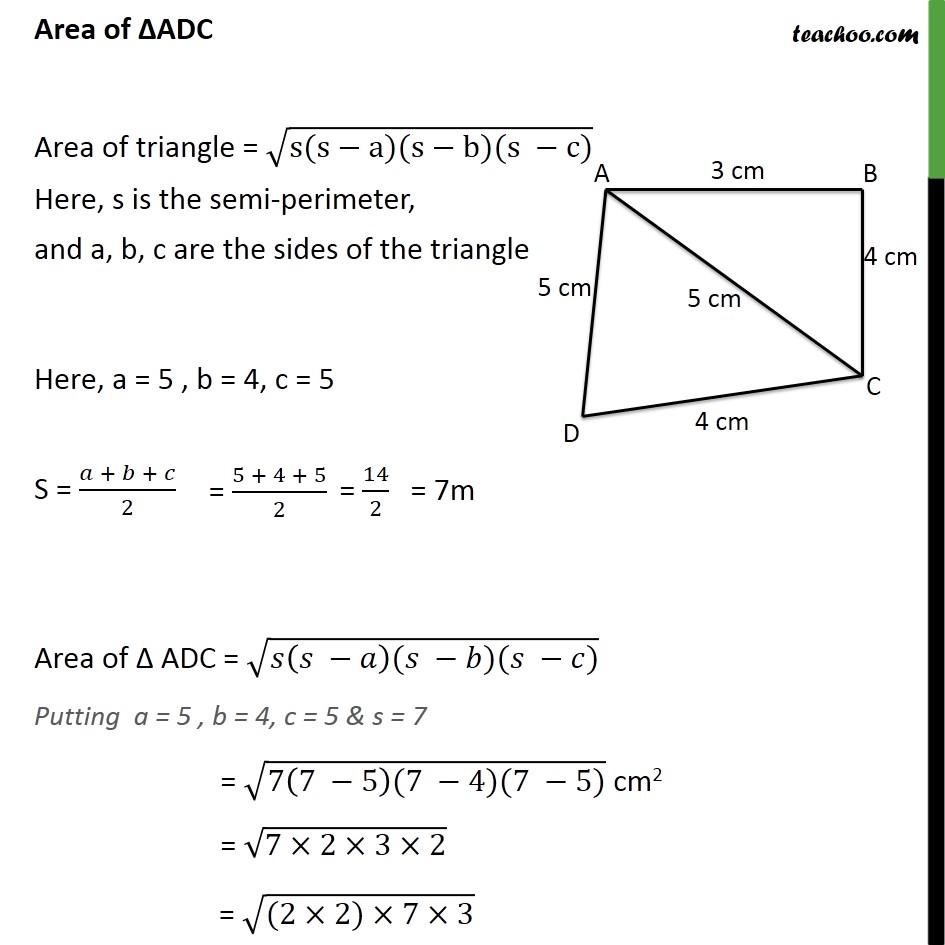
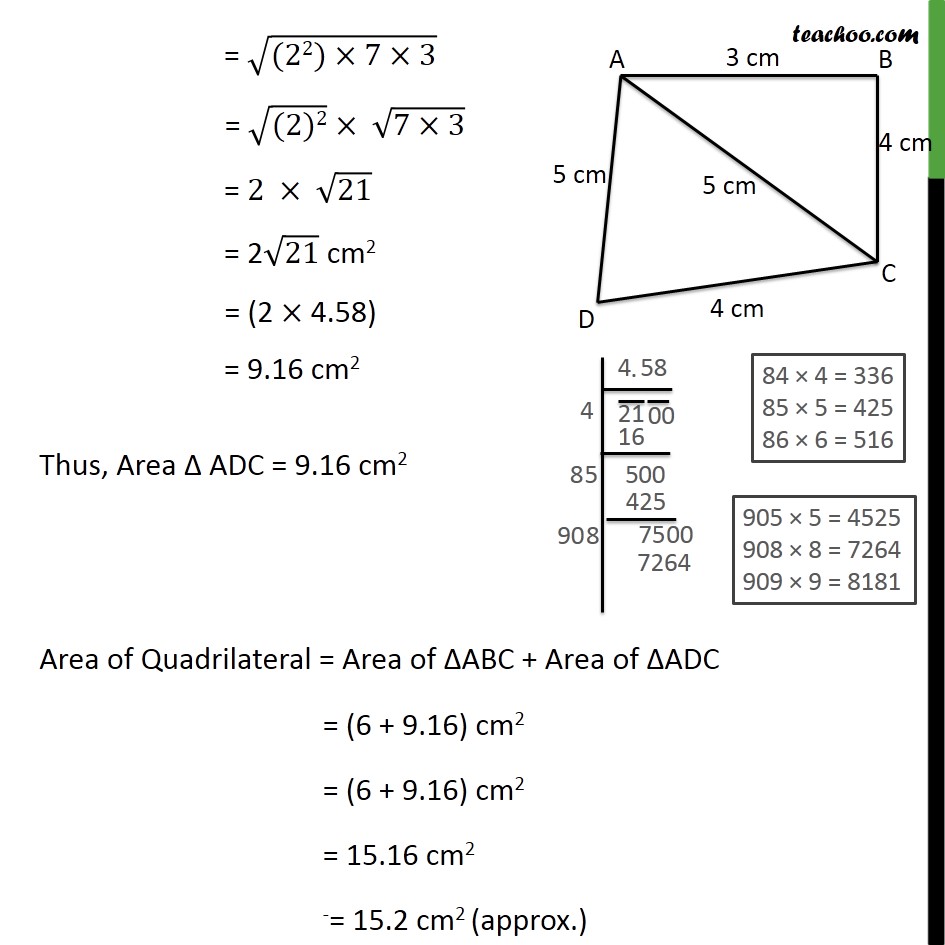
Ex 12.2, 2 Find the area of a quadrilateral ABCD in which AB = 3 cm, BC = 4 cm, CD = 4 cm, DA = 5 cm and AC = 5 cm. Area of Quadrilateral = Area of ΔABC + Area of ΔADC Area of ΔABC Area of triangle = √(s(s−a)(s−b)(s −c)) Here, s is the semi-perimeter, and a, b, c are the sides of the triangle Here, a = 3 , b = 4, c = 5 S = (𝑎 + 𝑏 + 𝑐)/2 Area of Δ ABC = √(𝑠(𝑠 −𝑎)(𝑠 −𝑏)(𝑠 −𝑐)) Putting a = 3 , b = 4, c = 5 & s = 6 = √(6(6 −3)(6 −4)(6 −5)) cm2 = √(6×3×2×1) cm2 = √(6×6) cm2 = √((6)2) = 6 cm2 ∴ Area of ΔABC = 6 cm2 Area of ΔADC Area of triangle = √(s(s−a)(s−b)(s −c)) Here, s is the semi-perimeter, and a, b, c are the sides of the triangle Here, a = 5 , b = 4, c = 5 S = (𝑎 + 𝑏 + 𝑐)/2 Area of Δ ADC = √(𝑠(𝑠 −𝑎)(𝑠 −𝑏)(𝑠 −𝑐)) Putting a = 5 , b = 4, c = 5 & s = 7 = √(7(7 −5)(7 −4)(7 −5)) cm2 = √(7×2×3×2) = √((2×2)×7×3) = √((22)×7×3) = √((2)2) × √(7×3) = 2 × √21 = 2√21 cm2 = (2 × 4.58) = 9.16 cm2 Thus, Area Δ ADC = 9.16 cm2 Area of Quadrilateral = Area of ΔABC + Area of ΔADC = (6 + 9.16) cm2 = (6 + 9.16) cm2 = 15.16 cm2 -= 15.2 cm2 (approx.)