


Finding area of triangle
Last updated at Feb. 24, 2025 by Teachoo




Transcript
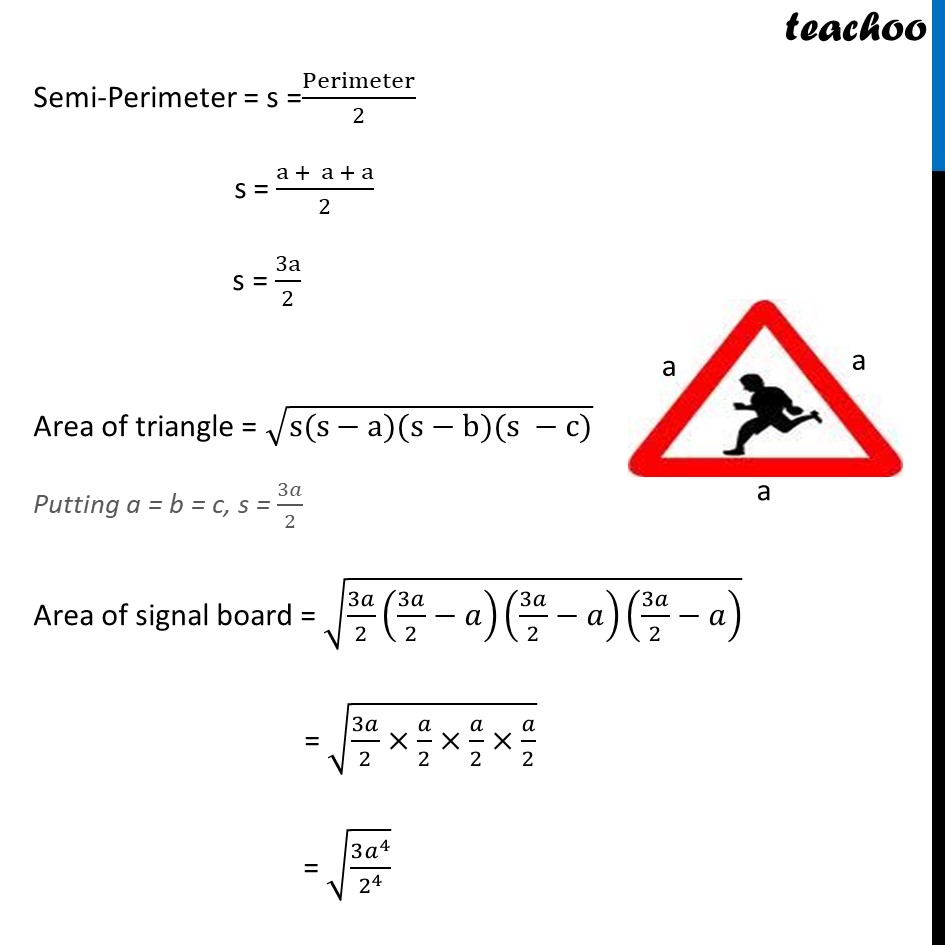
Ex 10.1, 1 A traffic signal board, indicating ‘SCHOOL AHEAD’, is an equilateral triangle with side ‘a’. Find the area of the signal board, using Heron’s formula. If its perimeter is 180 cm, what will be the area of the signal board? Area of triangle = √(s(s−a)(s−b)(s −c)) Here, s is the semi-perimeter, and a, b, c are the sides of the triangle Given Perimeter = 180 cm Semi-Perimeter = s =Perimeter/2 s = 180/2 s = 90 cm Given that the triangle is equilateral Since all sides of equilateral triangle are equal ∴ a = b = c Perimeter = 180 cm a + a + a = 180 cm 3a = 180 cm a = 180/3 cm a = 60 cm Area of triangle = √(s(s−a)(s−b)(s −c)) Putting a = b = c = 60 cm , s = 90 cm Area of signal board = √(90(90−60)(90−60)(90 −60)) = √( 90(30)(30)(30) ) = √( (9×3×3×3)×(10)4) = √((9×9)×3×(10)4) = √((92)×3×(10)4) = √92×√3 × √((10)4) = 9×√3 ×(〖104)〗^(1/2) = 9 ×√3 × (102) = 9 × 100 × √3 = 900√3 Thus, Area = 900√3 cm2