Question 1 - Case Based Questions (MCQ) - Chapter 2 Class 12 Inverse Trigonometric Functions

Transcript

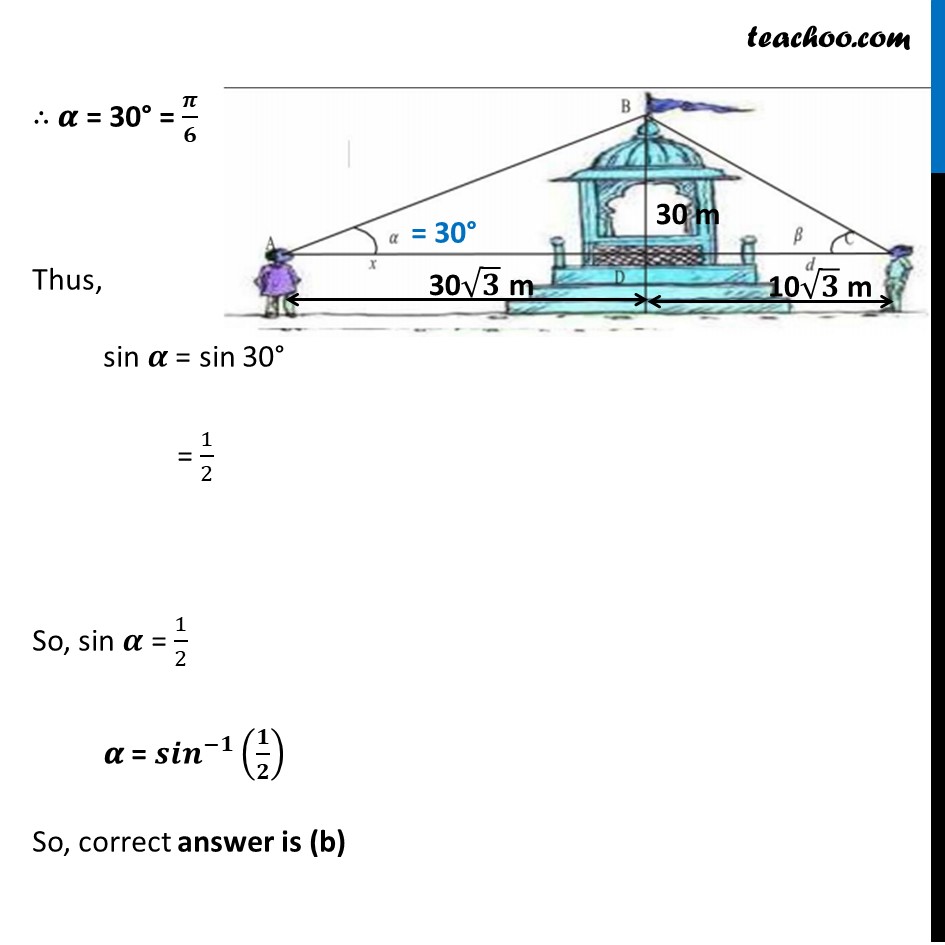
Two men on either side of a temple of 30 meters high observe its top at the angles of elevation 𝛼 and 𝛽 respectively. (as shown in the figure above). The distance between the two men is 40√3 meters and the distance between the first person A and the temple is 30 √3 meters. Based on the above information answer the following: Question 1 ∠CAB = 𝛼 = (a) 〖𝑠𝑖𝑛〗^(−1) (2/√3) (b) 〖𝑠𝑖𝑛〗^(−1) (1/2) (c) 〖𝑠𝑖𝑛〗^(−1) (2) (d) 〖𝑠𝑖𝑛〗^(−1) (√3/2) In Δ ABD tan 𝜶 = 𝐵𝐷/𝐴𝐷 tan 𝜶 = 30/(30√3) tan 𝜶 = 1/√3 ∴ 𝜶 = 30° = 𝝅/𝟔 Thus, sin 𝜶 = sin 30° = 1/2 So, sin 𝜶 = 1/2 𝜶 = 〖𝒔𝒊𝒏〗^(−𝟏) (𝟏/𝟐) So, correct answer is (b) Question 2 ∠CAB = 𝛼 = (a) 〖𝑐𝑜𝑠〗^(−1) (1/5) (b) 〖𝑐𝑜𝑠〗^(−1) (2/5) (c) 〖𝑐𝑜𝑠〗^(−1) (√3/2) (d) 〖𝑐𝑜𝑠〗^(−1) (4/5) Now, 𝜶 = 30° = 𝝅/𝟔 Thus, cos 𝜶 = cos 30° = √3/2 So, sin 𝜶 =√3/2 𝜶 = 〖𝑐𝑜𝑠〗^(−1) (√3/2) So, correct answer is (c) Question 3 ∠BCA = 𝛽 = (a) 〖𝑡𝑎𝑛〗^(−1) (1/2) (b) 〖𝑡𝑎𝑛〗^(−1) (2) (c) 〖𝑡𝑎𝑛〗^(−1) (1/√3) (d) 〖𝑡𝑎𝑛〗^(−1) (√3) In Δ ABD tan 𝛽 = 𝐵𝐷/𝐴𝐷 tan 𝛽 = 30/(10√3) tan 𝛽 = 3/√3 tan 𝛽 = √3 𝛽 = 〖𝑡𝑎𝑛〗^(−1) (√3) So, the correct answer is (d) Also, 𝛽 = 60° = 𝝅/𝟑 Question 4 ∠ABC = (a) 𝜋/4 (b) 𝜋/6 (c) 𝜋/2 (d) 𝜋/3 Since 𝜶 = 30° and 𝛽 = 60° In Δ ABC, By Angle sum property 𝜶 + 𝛽 + ∠ ABC = 180° 30° + 60° + ∠ ABC = 180° ∠ ABC = 90° ∠ ABC = 𝝅/𝟐 So, the correct answer is (c) Question 5 Domain and Range of cos−1 𝑥 = (a) (−1, 1), (0 , 𝜋) (b) [−1, 1], (0 , 𝜋) (c) [−1, 1], [0 , 𝜋] (d) (−1, 1), [−𝜋/2, 𝜋/2] Since cos x is defined at x = 0, and x = 𝜋 Domain of cos−1 𝑥 includes −1 and 1 Range of cos−1 𝑥 also includes 0 and 𝜋 So, the correct answer is (c)