Question 2 - Examples - Chapter 6 Class 9 Lines and Angles

Transcript

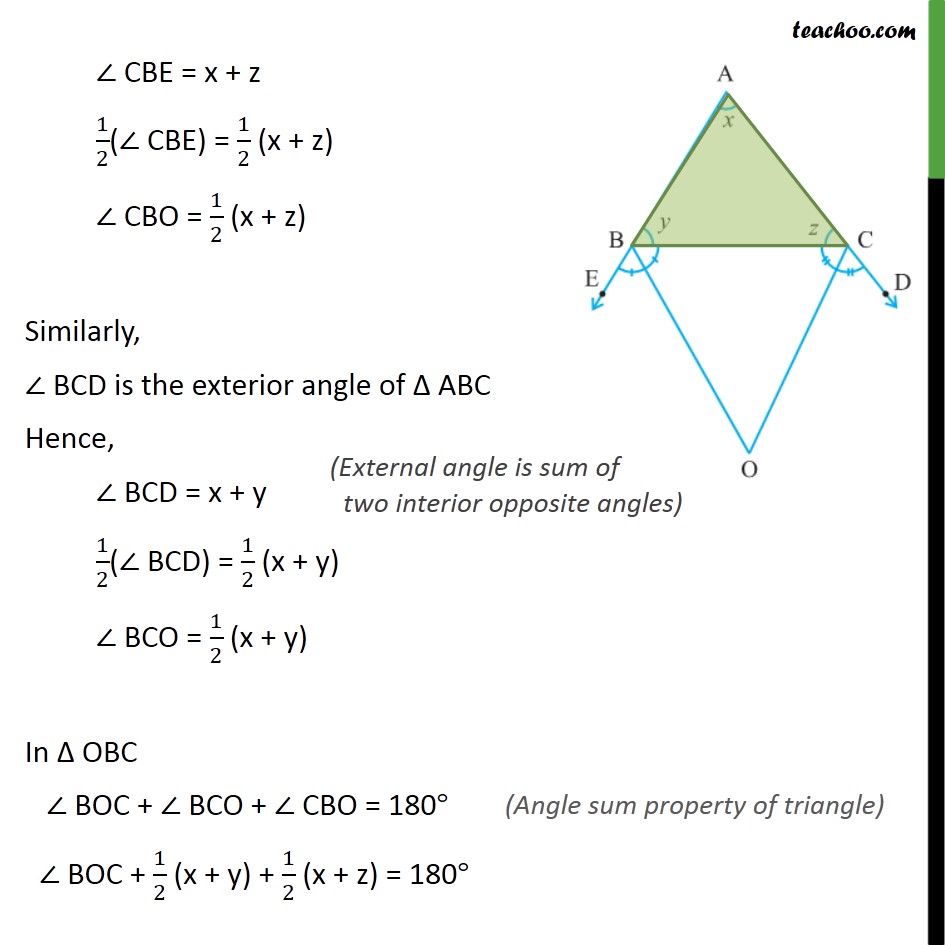
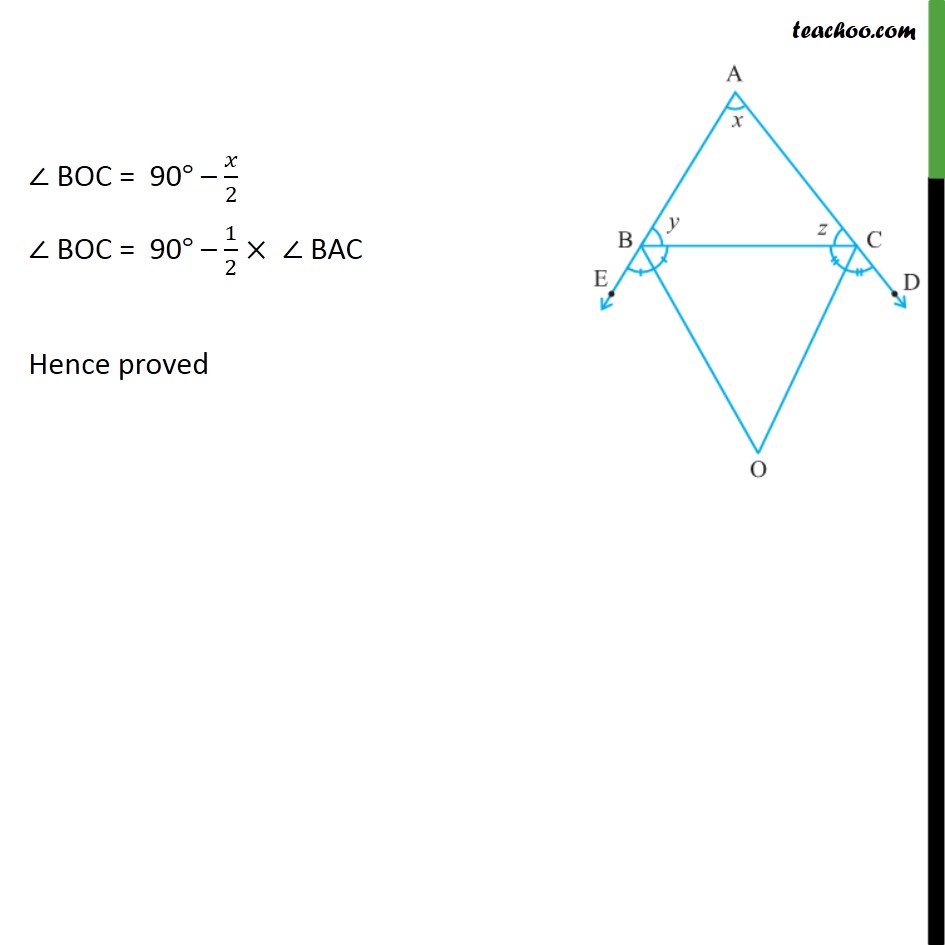
Question 2 In figure, the sides AB and AC of ∆ABC are produced to points E and D respectively. If bisectors BO and CO of ∠CBE and ∠BCD respectively meet at point O, then prove that ∠BOC = 90° − 1/2∠ BAC. BO is the bisector of ∠ CBE So, ∠ CBO = ∠ EBO = 1/2 ∠ CBE Similarly, CO is the bisector of ∠ BCD So, ∠ BCO = ∠ DCO = 1/2 ∠ BCD ∠ CBE is the exterior angle of Δ ABC Hence, ∠ CBE = x + z ∠ CBE = x + z 1/2(∠ CBE) = 1/2 (x + z) ∠ CBO = 1/2 (x + z) Similarly, ∠ BCD is the exterior angle of Δ ABC Hence, ∠ BCD = x + y 1/2(∠ BCD) = 1/2 (x + y) ∠ BCO = 1/2 (x + y) In Δ OBC ∠ BOC + ∠ BCO + ∠ CBO = 180° ∠ BOC + 1/2 (x + y) + 1/2 (x + z) = 180° ∠ BOC + 1/2 (x + y) + 1/2 (x + z) = 180° ∠ BOC + 1/2 (x + y + x + z) = 180° In Δ ABC x + y + z = 180° Putting (2) in (1) ∠ BOC + 1/2 (x + y + x + z) = 180° ∠ BOC + 1/2 (x + 180° ) = 180° ∠ BOC + 𝑥/2 + 1/2 × 180° = 180° ∠ BOC + 𝑥/2 + 90° = 180° ∠ BOC = 180° – 90° – 𝑥/2 ∠ BOC = 90° – 𝑥/2 ∠ BOC = 90° – 𝑥/2 ∠ BOC = 90° – 1/2 × ∠ BAC Hence proved