Example 5 - Chapter 6 Class 9 Lines and Angles

Transcript

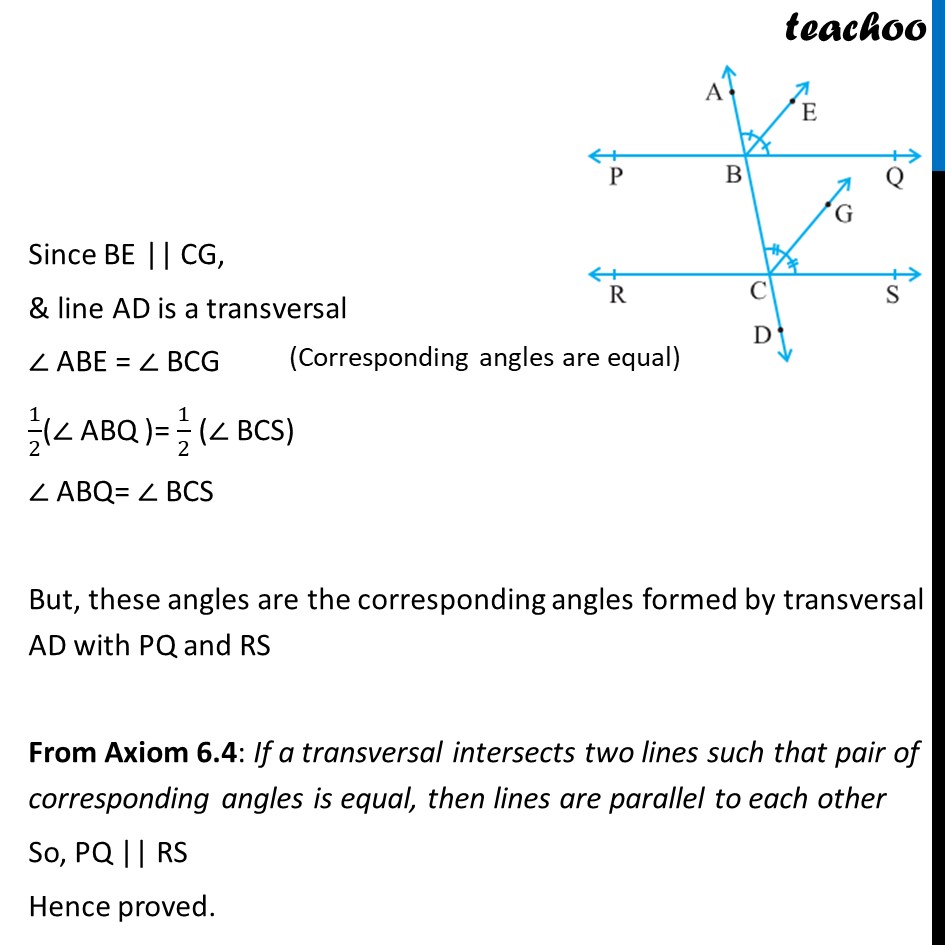
Example 5 If a transversal intersects two lines such that the bisectors of a pair of corresponding angles are parallel, then prove that the two lines are parallel. In figure, transversal AD intersects two lines PQ and RS at points B and C respectively. Ray BE is the bisector of BACQ So , ABE = EBQ = 1/2( ABQ ) and ray CG is the bisector of BCS; So , BCG = GCS = 1/2( BCS) and BE || CG. We have to prove PQ || RS Since BE || CG, & line AD is a transversal ABE = BCG 1/2( ABQ )= 1/2 ( BCS) ABQ= BCS But, these angles are the corresponding angles formed by transversal AD with PQ and RS From Axiom 6.4: If a transversal intersects two lines such that pair of corresponding angles is equal, then lines are parallel to each other So, PQ || RS Hence proved.