Ex 9.2, 3 - Chapter 9 Class 8 Algebraic Expressions and Identities

Transcript

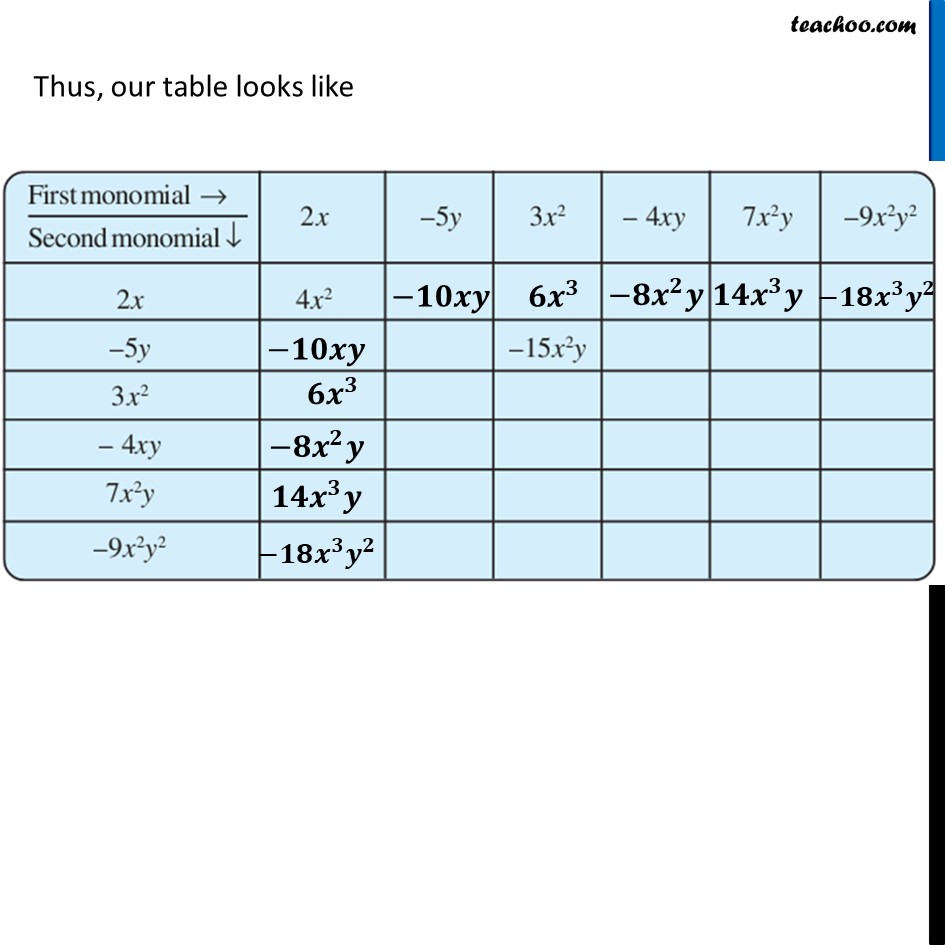
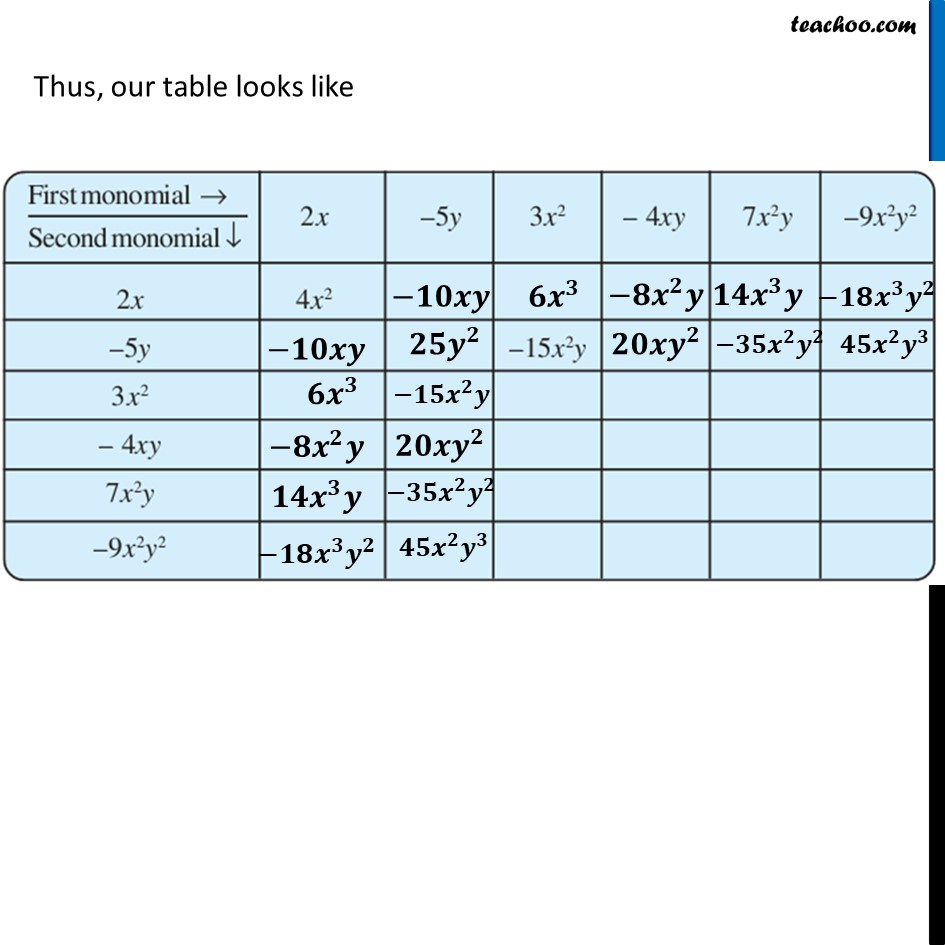
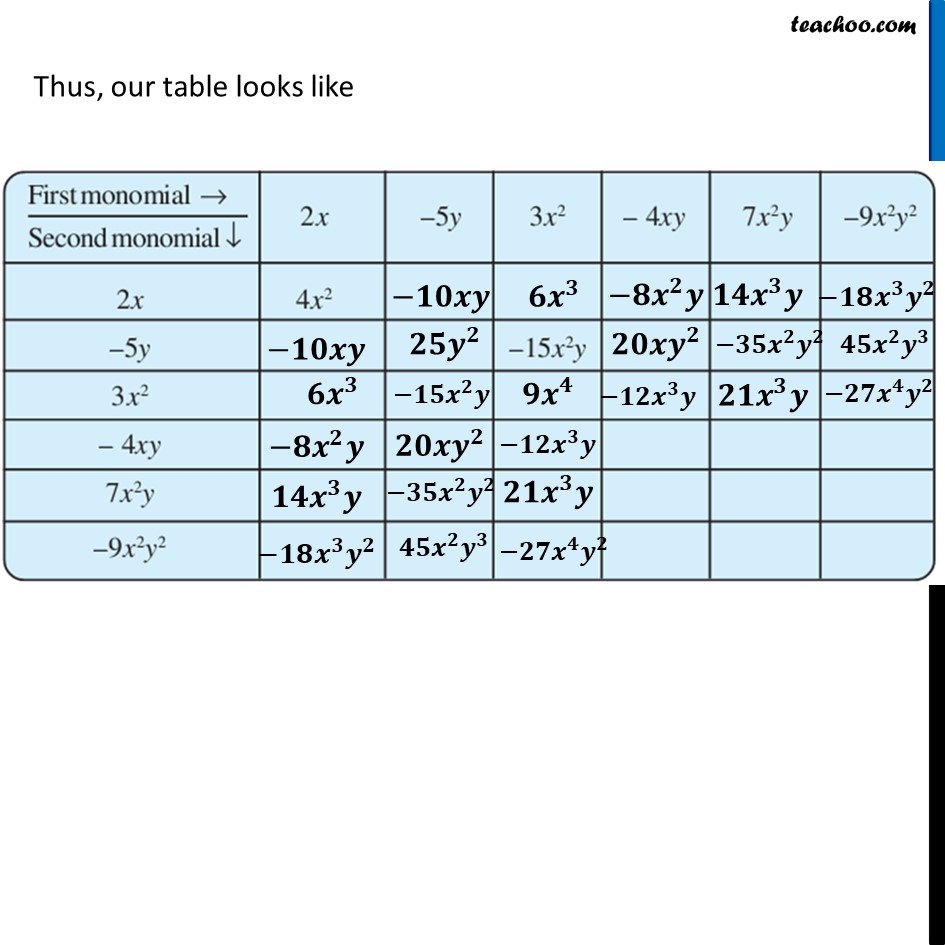
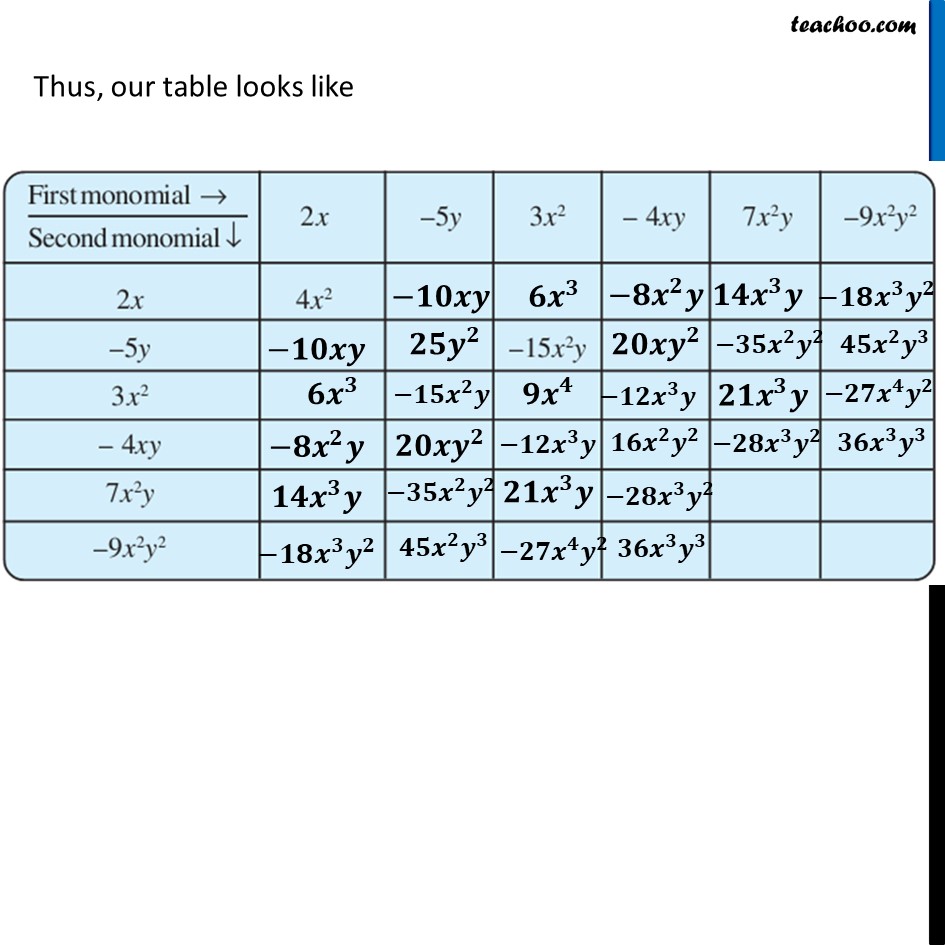
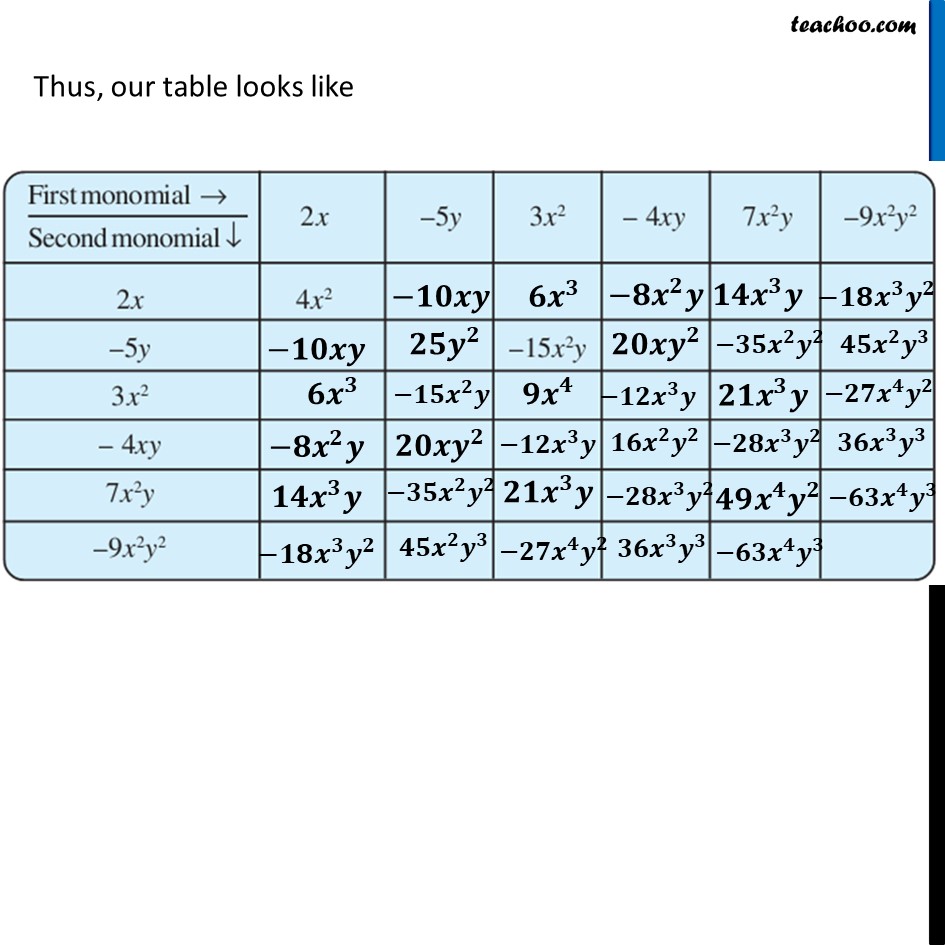
Ex 9.2, 3 Complete the table of products. For 2x 2𝑥×2𝑥 = 2×𝑥×2×𝑥 = (2×2)×(𝑥×𝑥) = 4 ×𝑥^2 = 4𝑥^2 Ex 9.2, 3 Complete the table of products. For 2x 2𝑥×−5𝑦 = 2×𝑥×−5×𝑦 = (2×−5)×𝑥×𝑦 = −10×𝑥×𝑦 = −10𝑥𝑦 Ex 9.2, 3 Complete the table of products. For 2x 2𝑥×3𝑥^2 = 2×𝑥×3×𝑥^2 = (2×3)×(𝑥×𝑥^2 ) = 6×𝑥^3 = 6𝑥^3 Ex 9.2, 3 Complete the table of products. For 2x 2𝑥×−4𝑥𝑦 = 2×𝑥×−4×𝑥×y = (2×−4)×(𝑥×𝑥)×𝑦 = −8×𝑥^2×𝑦 = −8𝑥^2 𝑦 Ex 9.2, 3 Complete the table of products. For 2x 2𝑥×7𝑥^2 𝑦 = 2×𝑥×7×𝑥^2×y = (2×7)×(𝑥×𝑥^2 )×𝑦 = 14×𝑥^3×𝑦 = 14𝑥^3 𝑦 Ex 9.2, 3 Complete the table of products. For 2x 2𝑥×−9𝑥^2 𝑦^2 = 2×𝑥×−9×𝑥^2×y^2 = (2×−9)×(𝑥×𝑥^2 )×𝑦^2 = −18×𝑥^3×𝑦^2 = −18𝑥^3 𝑦^2 Ex 9.2, 3 Complete the table of products. For –5y (−5𝑦)×2𝑥 = −5×𝑦×2×𝑥 = (−5×2)×(𝑦×𝑥) = −10×𝑥𝑦 = −10𝑥𝑦 Ex 9.2, 3 Complete the table of products. For –5y (−5𝑦)×(−5𝑦) = −5×𝑦×−5×𝑦 = (−5×−5)×(𝑦×𝑦) = 25×𝑦^2 = 25𝑦^2 Ex 9.2, 3 Complete the table of products. For –5y (−5𝑦)×3𝑥^2 = −5×𝑦×−5×𝑥^2 = (−5×3)×𝑦×𝑥^2 = −15×𝑥^2×𝑦 = −15𝑥^2 𝑦 Ex 9.2, 3 Complete the table of products. For –5y (−5𝑦)×(−4𝑥𝑦) = −5×𝑦×−4×𝑥×𝑦 = (−5×−4)×𝑦×𝑦×𝑥 = 20×𝑦^2×𝑥 = 20𝑦^2 𝑥 Ex 9.2, 3 Complete the table of products. For –5y (−5𝑦)×7𝑥^2 𝑦 = −5×𝑦×7×𝑥^2×𝑦 = (−5×7)×(𝑦×𝑦)×𝑥^2 = −35×𝑦^2×𝑥^2 = −35𝑦^2 𝑥^2 Ex 9.2, 3 Complete the table of products. For –5y (−5𝑦)×(−9𝑥^2 𝑦^2 ) = −5×𝑦×(−9)×𝑥^2×𝑦^2 = (−5×−9)×𝑥^2×(𝑦×𝑦^2 ) = 45×𝑥^2×𝑦^3 = 45𝑥^2 𝑦^3 Ex 9.2, 3 Complete the table of products. For 3x2 3𝑥^2×2𝑥 = 5×𝑥^2×2×𝑥 = (3×2)×(𝑥^2×𝑥) = 6×𝑥^3 = 6𝑥^3 Ex 9.2, 3 Complete the table of products. For 3x2 3𝑥^2×(−5𝑦) = 3×𝑥^2×−5×𝑦 = (3×−5)×𝑥^2×𝑦 = −15𝑥^2 𝑦^2 Ex 9.2, 3 Complete the table of products. For 3x2 3𝑥^2×3𝑥^2 = 3×𝑥^2×3×𝑥^2 = (3×3)×(𝑥^2×𝑥^2 ) = 9×𝑥^4 = 9𝑥^4 Ex 9.2, 3 Complete the table of products. For 3x2 3𝑥^2×(−4𝑥𝑦) = 3×𝑥^2×−4×𝑥×𝑦 = (3×−4)×(𝑥^2×𝑥)×𝑦 = −12×𝑥^3×𝑦 = −12𝑥^3 𝑦 Note: 𝑥𝑎 ×𝑥𝑏 = 𝑥^(𝑎 + 𝑏) Ex 9.2, 3 Complete the table of products. For 3x2 3𝑥^2×7𝑥^2 𝑦 = 3×𝑥^2×7×𝑥^2×𝑦 = (3×7)×(𝑥^2×𝑥^2 )×𝑦 = 21×𝑥^4×𝑦 = 21𝑥^4 𝑦 Ex 9.2, 3 Complete the table of products. For 3x2 3𝑥^2×(−9𝑥^2 𝑦^2) = 3×𝑥^2×7×𝑥^2×𝑦 = (3×−9)×(𝑥^2×𝑥^2 )×𝑦^2 = −27×𝑥^4×𝑦^2 = −27𝑥^4 𝑦^2 Ex 9.2, 3 Complete the table of products. For −𝟒𝒙𝒚 (−4𝑥𝑦)×2𝑥 = −4×𝑥×𝑦×2×𝑥 = (−4×2)×(𝑥×𝑥)×𝑦 = −8×𝑥^2×𝑦 = −8𝑥^2 𝑦 Ex 9.2, 3 Complete the table of products. For −𝟒𝒙𝒚 (−4𝑥𝑦)×(−5𝑦) = −4×𝑥×𝑦×−5×𝑦 = (−4×−5)×𝑥×(𝑦×𝑦) = 20×𝑥×𝑦^2 = 20𝑥𝑦^2 Ex 9.2, 3 Complete the table of products. For −𝟒𝒙𝒚 (−4𝑥𝑦)×3𝑥^2 = −4×𝑥×𝑦×3×𝑥^2 = (−4×3)×(𝑥×𝑥^2 )×𝑦 = −12×𝑥^3×𝑦 = −12𝑥^3 𝑦 Ex 9.2, 3 Complete the table of products. For −𝟒𝒙𝒚 (−4𝑥𝑦)×(−4𝑥𝑦) = −4×𝑥×𝑦×−4×𝑥×𝑦 = (−4×−4)×(𝑥×𝑥)×(𝑦×𝑦) = 16×𝑥^2×𝑦^2 = 16𝑥^2 𝑦^2 Ex 9.2, 3 Complete the table of products. For −𝟒𝒙𝒚 (−4𝑥𝑦)×7𝑥^2 𝑦 = −4×𝑥×𝑦×7×𝑥^2×𝑦 = (−4×7)×(𝑥×𝑥^2 )×(𝑦×𝑦) = −28×𝑥^3×𝑦^2 = −28𝑥^3 𝑦^2 Ex 9.2, 3 Complete the table of products. For −𝟒𝒙𝒚 (−4𝑥𝑦)×(−9𝑥^2 𝑦^2 ) = −4×𝑥×𝑦×−9×𝑥^2×𝑦^2 = (−4×−9)×(𝑥×𝑥^2 )×(𝑦×𝑦^2 ) = 36×𝑥^3×𝑦^3 = 36𝑥^3 𝑦^3 Ex 9.2, 3 Complete the table of products. For 𝟕𝒙^𝟐 𝒚 (7𝑥^2 𝑦)×2𝑥 = 7×𝑥^2×𝑦×2×𝑥 = (7×2)×(𝑥^2×𝑥)×𝑦 = 14×𝑥^3×𝑦 = 14𝑥^3 𝑦 Ex 9.2, 3 Complete the table of products. For 𝟕𝒙^𝟐 𝒚 (7𝑥^2 𝑦)×(−5𝑦) = 7×𝑥^2×𝑦×−5×𝑦 = (7×−5)×𝑥^2×(𝑦×𝑦) = −35×𝑥^2×𝑦^2 = −35𝑥^2 𝑦^2 Ex 9.2, 3 Complete the table of products. For 𝟕𝒙^𝟐 𝒚 (7𝑥^2 𝑦)×3𝑥^2 = 7×𝑥^2×𝑦×3×𝑥^2 = (7×3)×(𝑥^2×𝑥^2 )×𝑦 = 21×𝑥^4×𝑦 = 21𝑥^4 𝑦 Ex 9.2, 3 Complete the table of products. For 𝟕𝒙^𝟐 𝒚 (7𝑥^2 𝑦)×(−4𝑥𝑦) = 7×𝑥^2×𝑦×−4×𝑥×𝑦 = (7×−4)×(𝑥^2×𝑥)×(𝑦×𝑦) = −28×𝑥^3×𝑦^2 = −28𝑥^3 𝑦^2 Ex 9.2, 3 Complete the table of products. For 𝟕𝒙^𝟐 𝒚 (7𝑥^2 𝑦)×(7𝑥^2 𝑦) = 7×𝑥^2×𝑦×7×𝑥^2×𝑦 = (7×7)×(𝑥^2×𝑥^2 )×(𝑦×𝑦) = 49×𝑥^4×𝑦^2 = 49𝑥^4 𝑦^2 Ex 9.2, 3 Complete the table of products. For 𝟕𝒙^𝟐 𝒚 (7𝑥^2 𝑦)×(−9𝑥^2 𝑦^2 ) = 7×𝑥^2×𝑦×−9×𝑥^2×𝑦^2 = (7×−9)×(𝑥^2×𝑥^2 )×(𝑦×𝑦^2 ) = −63×𝑥^4×𝑦^3 = −63𝑥^4 𝑦^3 Ex 9.2, 3 Complete the table of products. For −𝟗𝒙^𝟐 𝒚^𝟐 (−9𝑥^2 𝑦^2 )×2𝑥 = −9×𝑥^2×𝑦^2×2×𝑥 = (−9×2)×(𝑥^2×𝑥)×𝑦^2 = −18×𝑥^3×𝑦^2 = −18𝑥^3 𝑦^2 Ex 9.2, 3 Complete the table of products. For −𝟗𝒙^𝟐 𝒚^𝟐 (−9𝑥^2 𝑦^2 )×−5𝑦 = −9×𝑥^2×𝑦^2×−5×𝑦 = (−9×−5)×𝑥^2×(𝑦^2×𝑦) = 45×𝑥^2×𝑦^3 = 45𝑥^2 𝑦^3 Ex 9.2, 3 Complete the table of products. For −𝟗𝒙^𝟐 𝒚^𝟐 (−9𝑥^2 𝑦^2 )×(3𝑥^2) = −9×𝑥^2×𝑦^2×3×𝑥^2 = (−9×3)×(𝑥^2×𝑥^2 )×𝑦^2 = −27×𝑥^4×𝑦^2 = −27𝑥^4 𝑦^2 Ex 9.2, 3 Complete the table of products. For −𝟗𝒙^𝟐 𝒚^𝟐 (−9𝑥^2 𝑦^2 )×(−4𝑥𝑦) = −9×𝑥^2×𝑦^2×−4×𝑥×𝑦 = (−9×−4)×(𝑥^2×𝑥)×(𝑦^2×𝑦) = 36×𝑥^3×𝑦^3 = 36𝑥^3 𝑦^3 Ex 9.2, 3 Complete the table of products. For −𝟗𝒙^𝟐 𝒚^𝟐 (−9𝑥^2 𝑦^2 )×7𝑥^2 𝑦 = −9×𝑥^2×𝑦^2×7×𝑥^2×𝑦 = (−9×7)×(𝑥^2×𝑥^2 )×(𝑦^2×𝑦) = −63×𝑥^4×𝑦^3 = −63𝑥^4 𝑦^3 Ex 9.2, 3 Complete the table of products. For −𝟗𝒙^𝟐 𝒚^𝟐 (−9𝑥^2 𝑦^2 )×(−9𝑥^2 𝑦^2 ) = −9×𝑥^2×𝑦^2×−9×𝑥^2×𝑦^2 = (−9×−9)×(𝑥^2×𝑥^2 )×(𝑦^2×𝑦^2 ) = 81×𝑥^4×𝑦^4 = 81𝑥^4 𝑦^4 Note: 𝑥𝑎 ×𝑥𝑏 = 𝑥^(𝑎 + 𝑏) So, the completed table looks like