



Last updated at Dec. 16, 2024 by Teachoo










Transcript
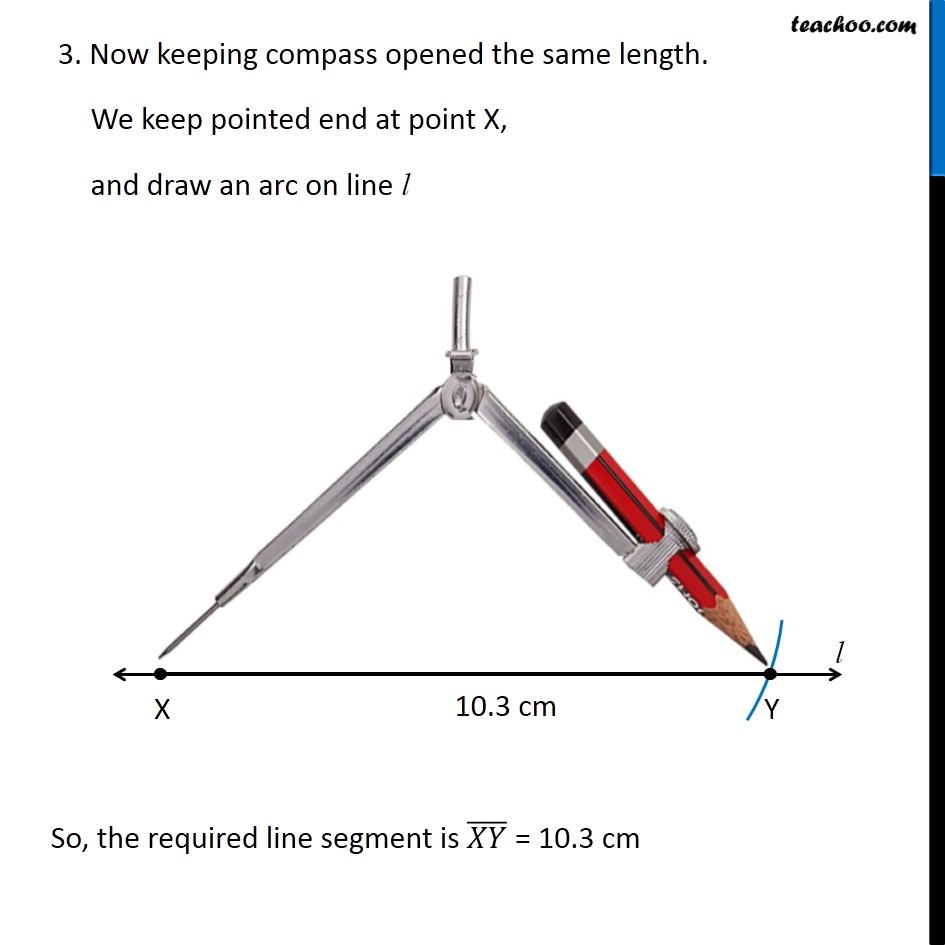
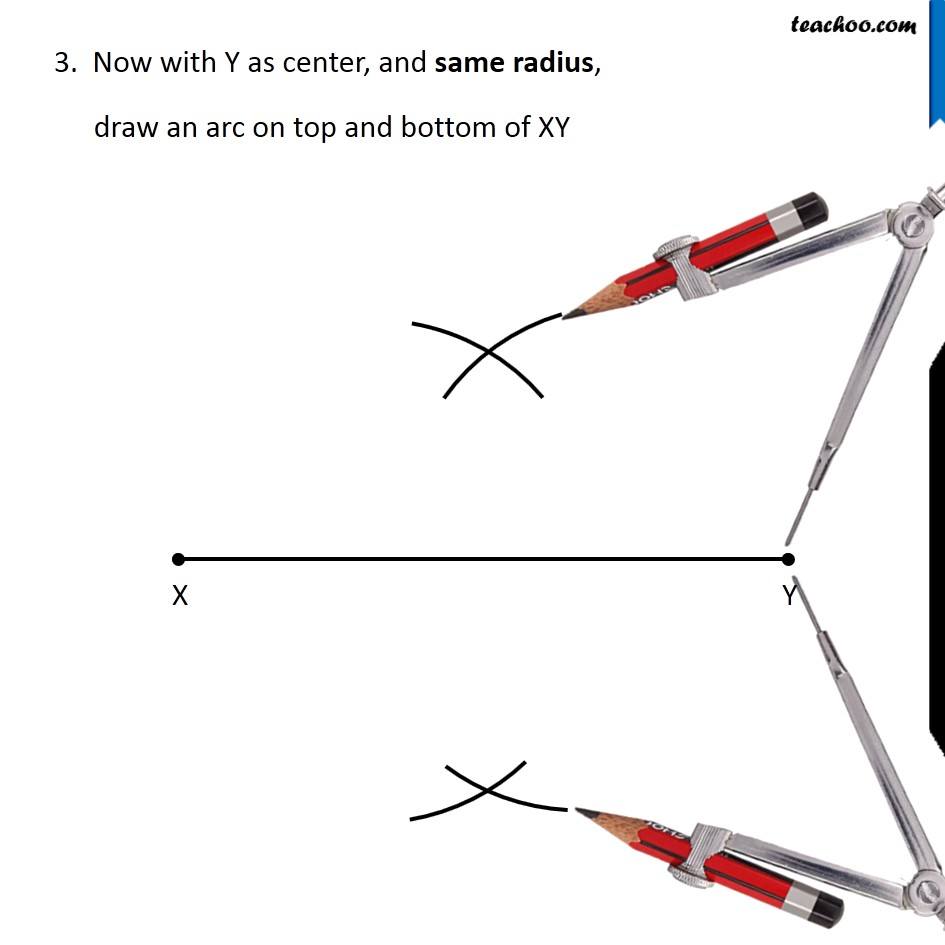
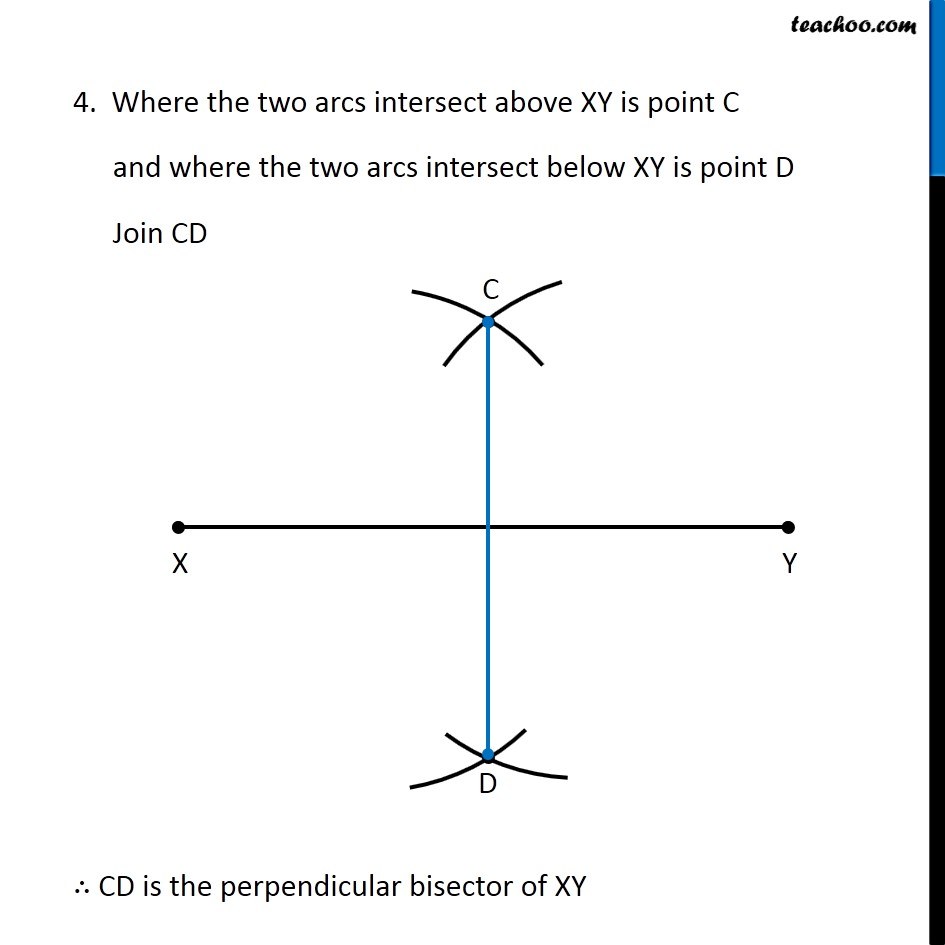
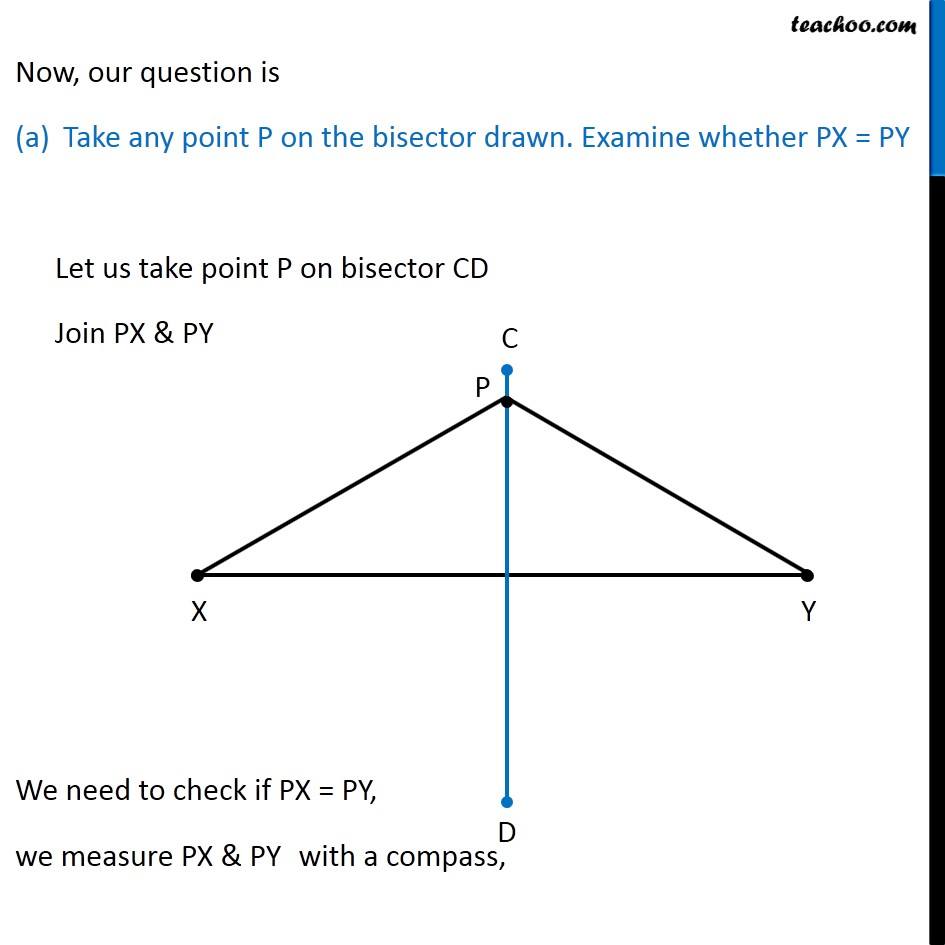
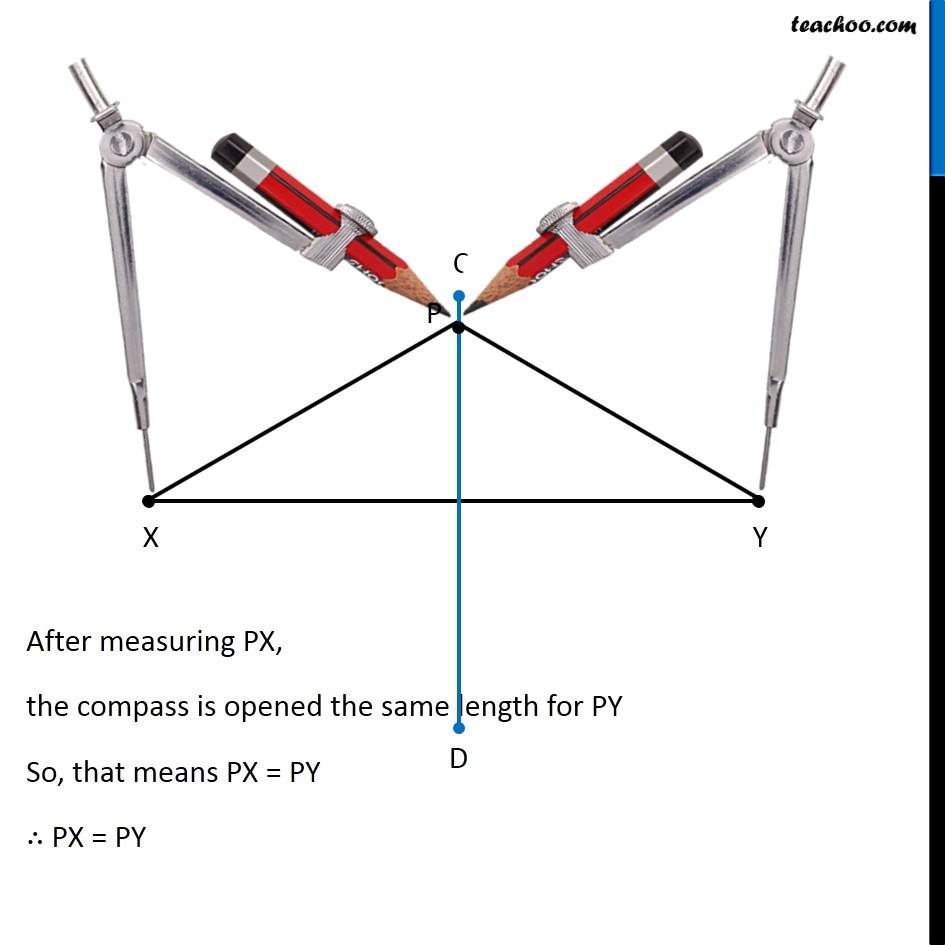
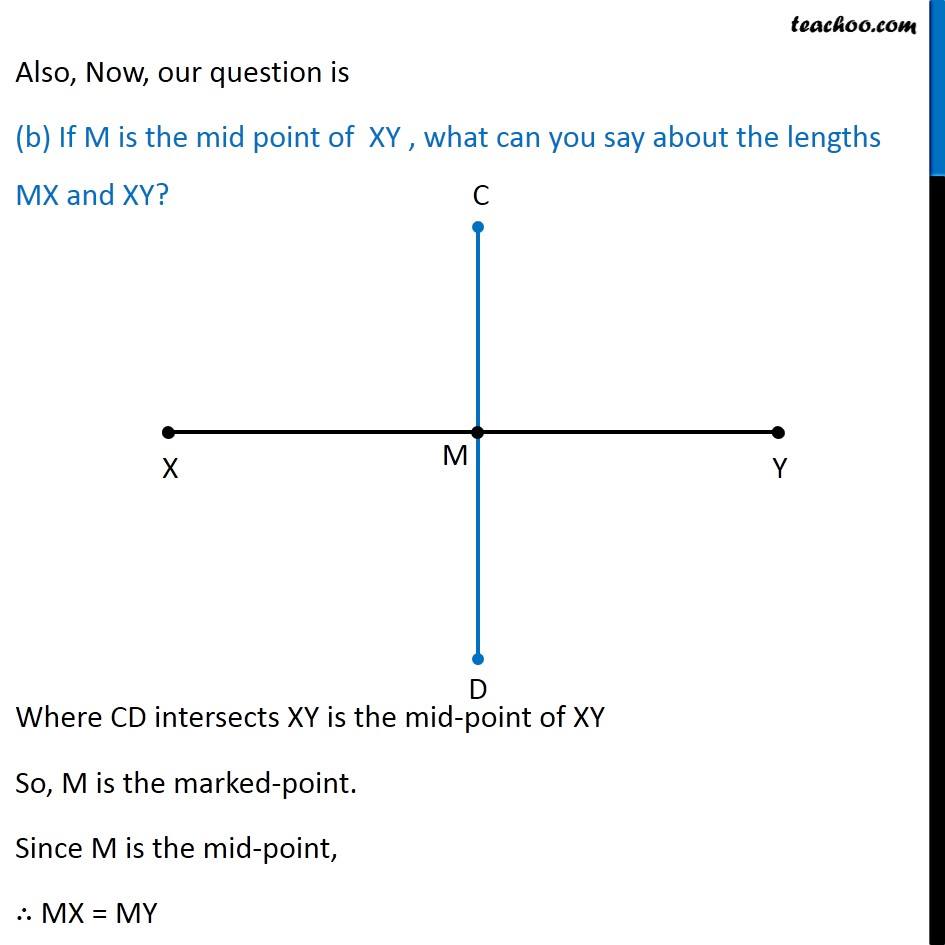
Question 3 Draw the perpendicular bisector of (𝑋𝑌) ̅whose length is 10.3 cm. (a) Take any point P on the bisector drawn. Examine whether PX = PY. (b) If M is the mid point (𝑋𝑌) ̅, what can you say about the lengths MX and XY? Let’s first draw a line segment of length 10.3 cm We follow these steps 1. Draw a line l mark point X on it 2. Since length is 10.3 cm, we measure 10.3 cm using ruler and compass 3. Now keeping compass opened the same length. We keep pointed end at point X, and draw an arc on line l So, the required line segment is (𝑋𝑌) ̅ = 10.3 cm Now, we need to make its perpendicular bisector Let’s follow these steps to make perpendicular bisector of XY 1. Given a line segment XY. 2. Now with X as center, and radius more than half XY, draw an arc on top and bottom of XY 3. Now with Y as center, and same radius, draw an arc on top and bottom of XY 4. Where the two arcs intersect above XY is point C and where the two arcs intersect below XY is point D Join CD ∴ CD is the perpendicular bisector of XY Now, our question is Take any point P on the bisector drawn. Examine whether PX = PY Let us take point P on bisector CD Join PX & PY We need to check if PX = PY, we measure PX & PY with a compass, After measuring PX, the compass is opened the same length for PY So, that means PX = PY ∴ PX = PY Also, Now, our question is (b) If M is the mid point of XY , what can you say about the lengths MX and XY? Where CD intersects XY is the mid-point of XY So, M is the marked-point. Since M is the mid-point, ∴ MX = MY