Ex 11.1, 11 - Chapter 11 Class 6 Algebra

Transcript

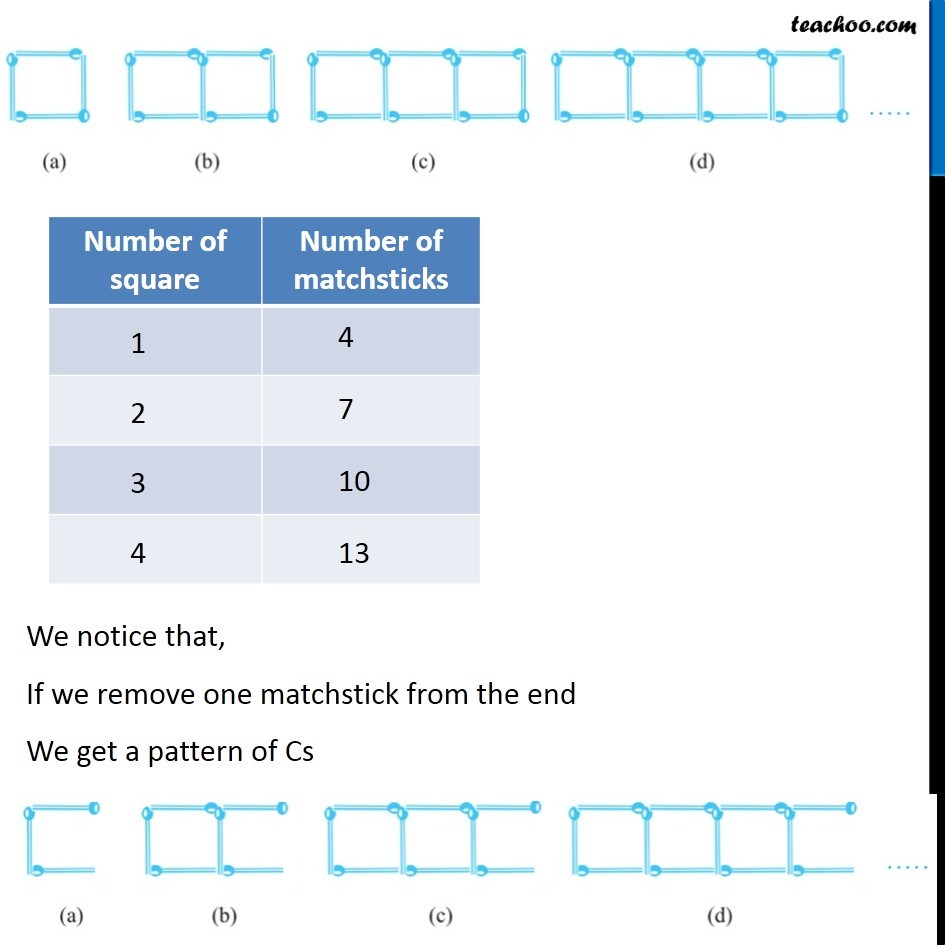
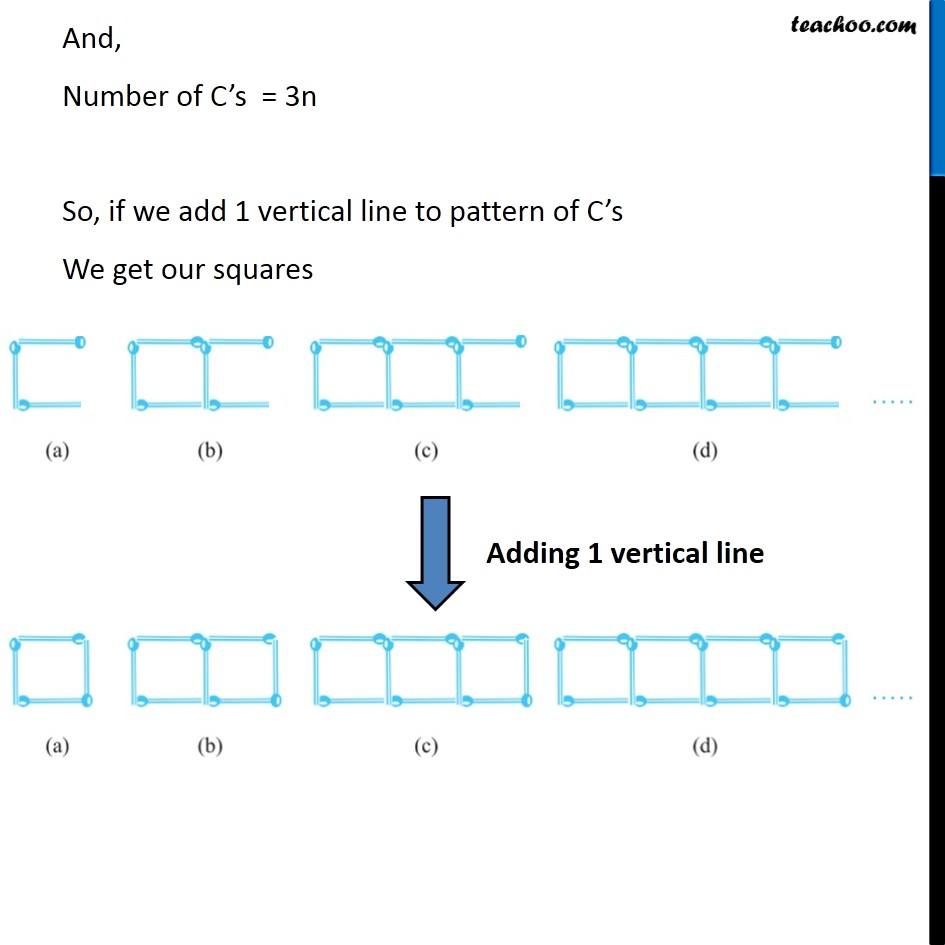
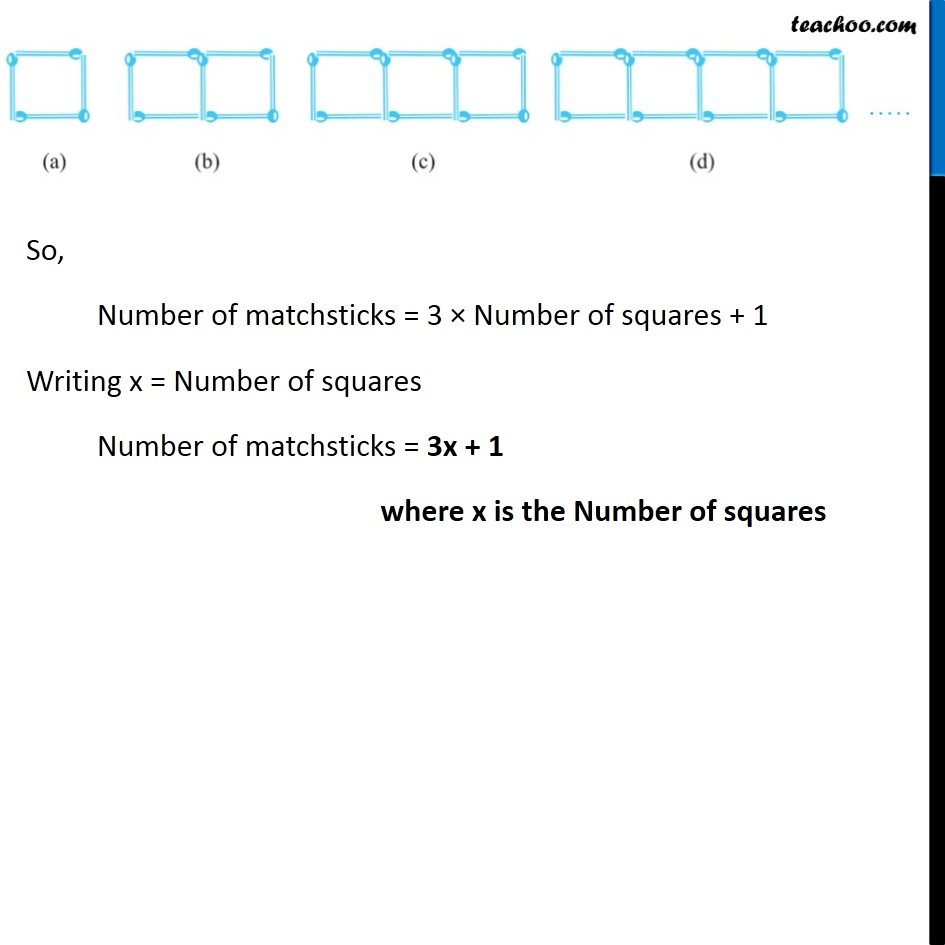
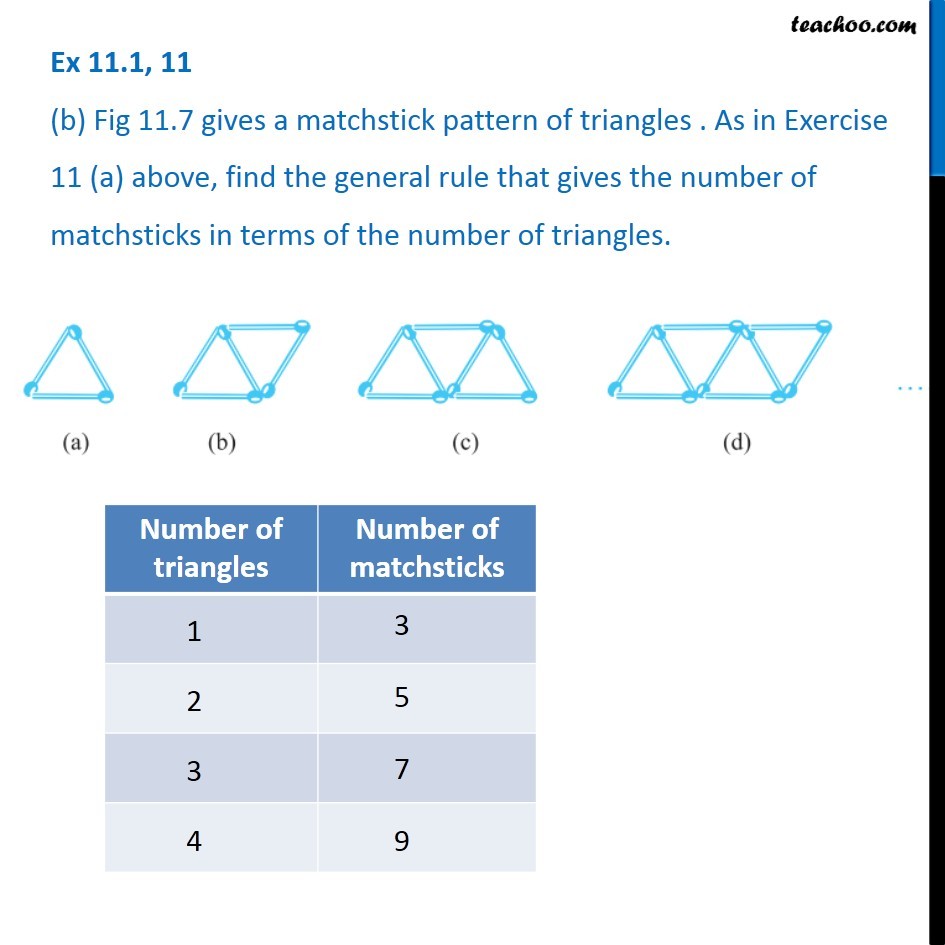
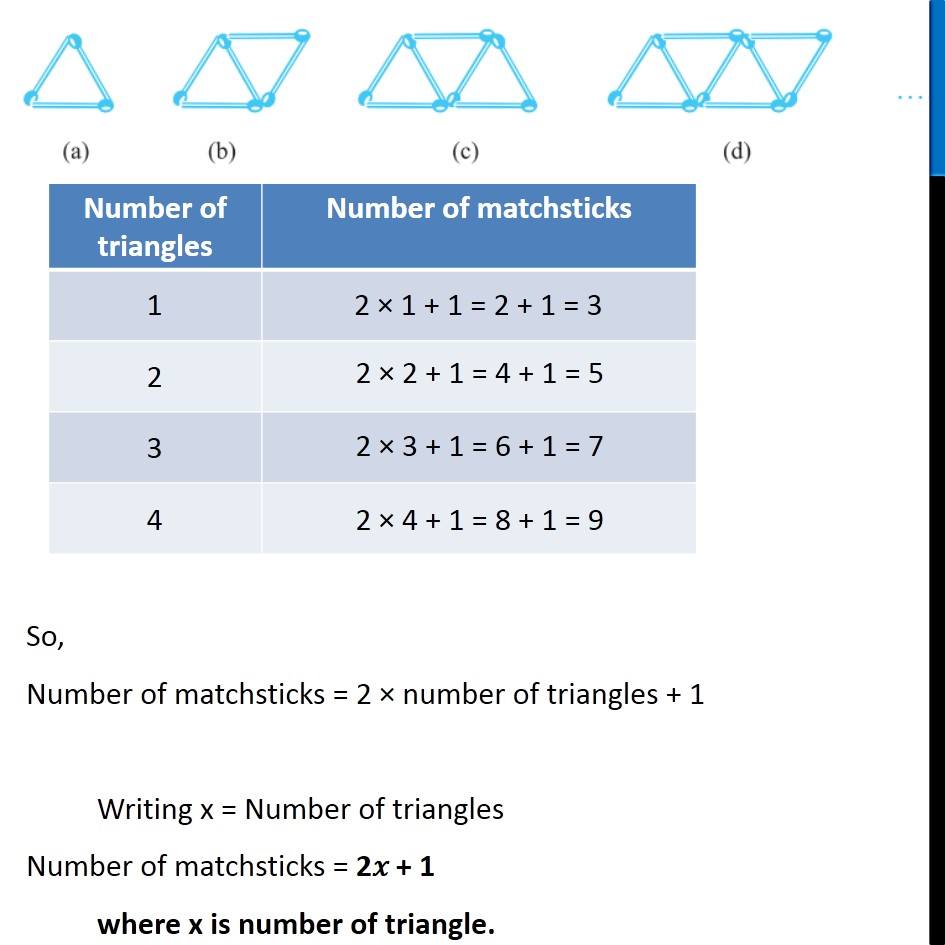
Ex 11.1, 11 (a) Look at the following matchstick pattern of squares (Fig 11.6). The squares are not separate. Two neighbouring squares have a common matchstick. Observe the patterns and find the rule that gives the number of matchsticks in terms of the number of squares. (Hint : If you remove the vertical stick at the end, you will get a pattern of Cs.) We notice that, If we remove one matchstick from the end We get a pattern of Cs We notice that, If we remove one matchstick from the end We get a pattern of Cs And, Number of C’s = 3n So, if we add 1 vertical line to pattern of C’s We get our squares So, Number of matchsticks = 3 × Number of squares + 1 Writing x = Number of squares Number of matchsticks = 3x + 1 where x is the Number of squares Ex 11.1, 11 (b) Fig 11.7 gives a matchstick pattern of triangles . As in Exercise 11 (a) above, find the general rule that gives the number of matchsticks in terms of the number of triangles. . We see that, 1st triangle requires 3 matchsticks 2nd triangle requires 3 matchsticks of 1st triangle & 2 new matchsticks 3rd triangle requires 3 matchsticks of 1st triangle & 2 new matchsticks of 2nd triangle & 2 new matchsticks of So, every new triangle requires 2 matchsticks for each triangle & 1 additional matchstick So, Number of matchsticks = 2 × number of triangles + 1 Writing x = Number of triangles Number of matchsticks = 2𝑥 + 1 where x is number of triangle.