Ex 3.2, 6 - Chapter 3 Class 8 Understanding Quadrilaterals

Transcript

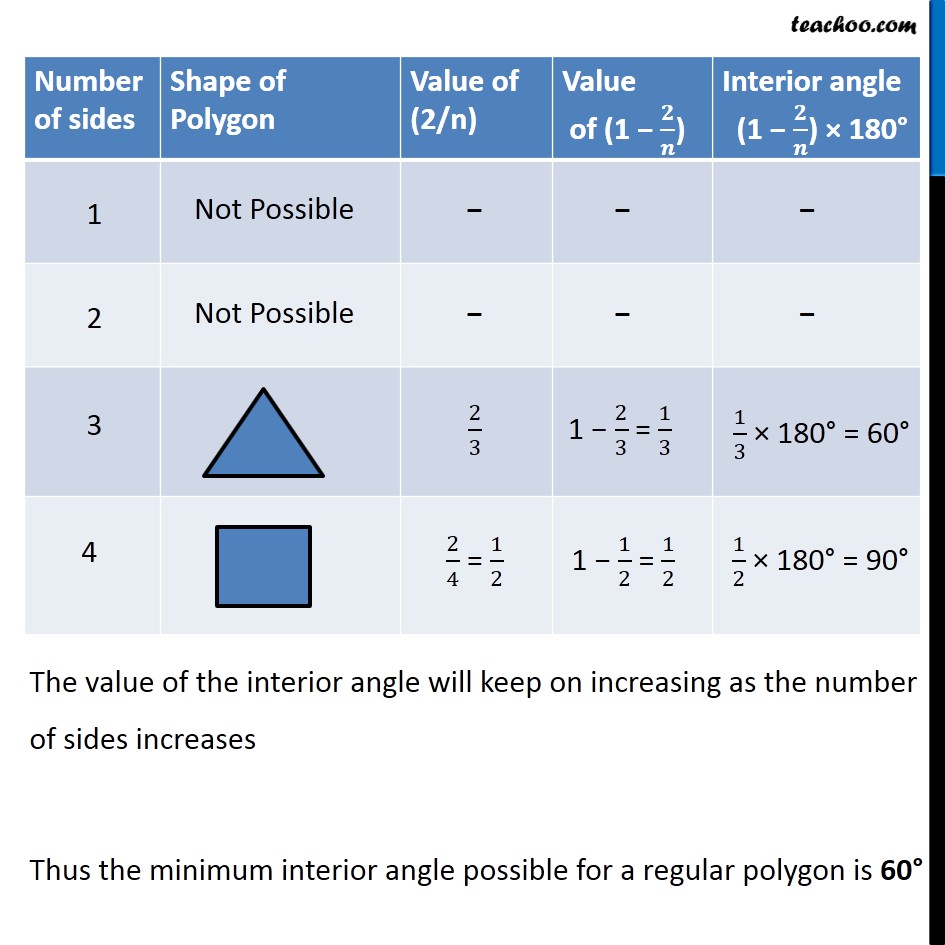
Ex 3.2, 6(a) What is the minimum interior angle possible for a regular polygon? Why?We know that Sum of angles of a regular polygon = Number of sides × interior angle (n − 2) 180° = n × interior angle Interior angle = ((𝑛 − 2))/𝑛 × 180° Interior angle = (1−2/𝑛) × 180° For the interior angle to be minimum, (1−2/𝑛) should be minimum. The value of the interior angle will keep on increasing as the number of sides increases Thus the minimum interior angle possible for a regular polygon is 60° Ex 3.2, 6(b) What is the maximum exterior angle possible for a regular polygon? We know that Sum of angles of a Regular Polygon = Number of sides × Exterior angle 360° = n × Exterior angle (360°)/𝑛 = Exterior angle Exterior angle = (360°)/𝑛 For exterior angle to be maximum, (1/𝑛) Should be minimum. The Measure of the exterior angle will decrease as number of sides increases ∴ Maximum exterior angle possible for a regular Polygon is 120°