Ex 5.4, 4 (Optional) - Chapter 5 Class 10 Arithmetic Progressions

Transcript

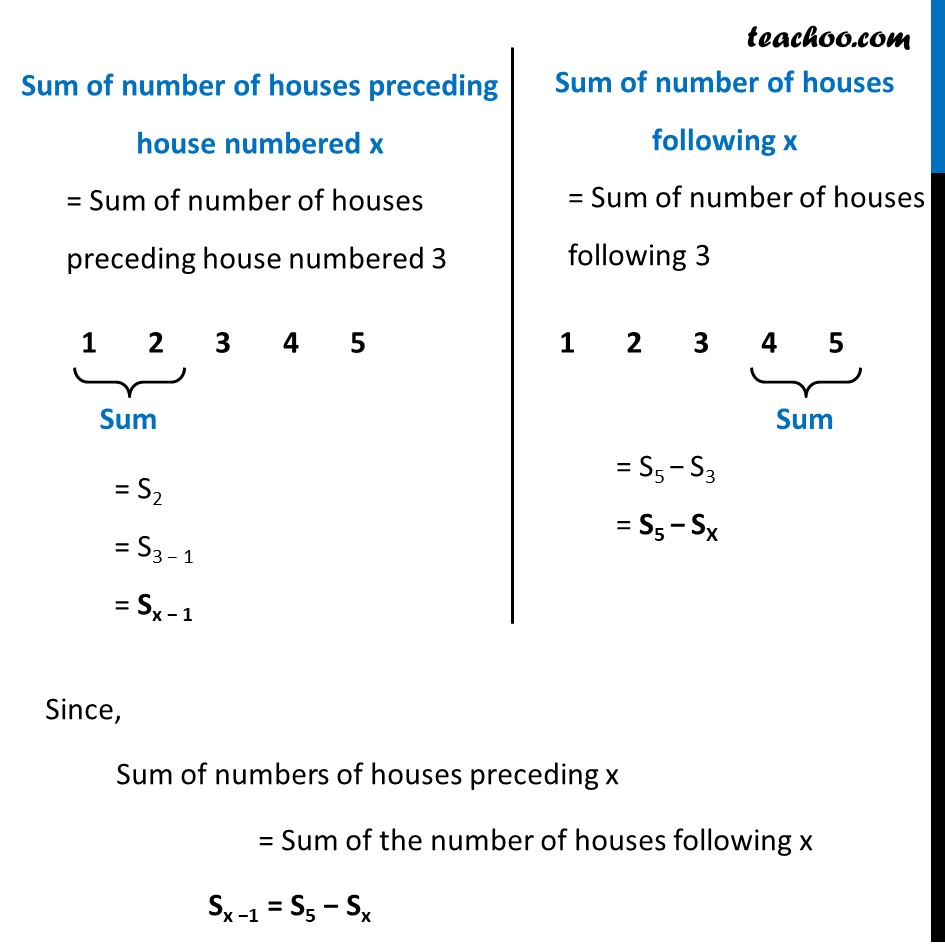
Ex 5.4, 4 (Optional) - Introduction The houses of a row are numbered consecutively from 1 to 49. Show that there is a value of x such that the sum of the numbers of the houses preceding the house numbered x is equal to the sum of the numbers of the houses following it. Find this value of x. [Hint : Sx – 1 = S49 – Sx] Introduction: Let 5 houses numbered from 1 to 5 be arranged in a row 1 2 3 4 5 Now, let x = 3 Then Sum of number of houses preceding house numbered x = Sum of number of houses preceding house numbered 3 = S2 = S3 − 1 = Sx − 1 Sum of number of houses following x = Sum of number of houses following 3 = S5 − S3 = S5 − SX Since, Sum of numbers of houses preceding x = Sum of the number of houses following x Sx −1 = S5 − Sx Ex 5.4, 4 (Optional) The houses of a row are numbered consecutively from 1 to 49. Show that there is a value of x such that the sum of the numbers of the houses preceding the house numbered x is equal to the sum of the numbers of the houses following it. Find this value of x. [Hint : Sx – 1 = S49 – Sx] Since, Sum of numbers of houses preceding x = Sum of the number of houses following x Sx−1 = S49 − Sx ((𝑥 − 1)(𝑥 − 1 + 1))/2 = (49 (49 + 1))/2 − (𝑥 (𝑥 + 1))/2 Sum of first n natural numbers = Sn = (𝒏(𝒏 + 𝟏))/𝟐 (𝑥(𝑥 − 1) )/2 = (49 × 50 )/2 − (𝑥 (𝑥 + 1))/2 1/2 [𝑥(𝑥−1)] = 1/2 [2450−𝑥(𝑥+1)] x(x − 1) = 2450 − x(x + 1) x2 − x = 2450 − x2 − x x2 − x + x2 + x = 2450 2x2 = 2450 x2 = 1225 x = ± √𝟏𝟐𝟐𝟓 x = ± √(52" × 72" ) x = ± √352 x = ± 35 Since number of houses can’t be negative ∴ x = 35