

Last updated at Dec. 16, 2024 by Teachoo






Transcript
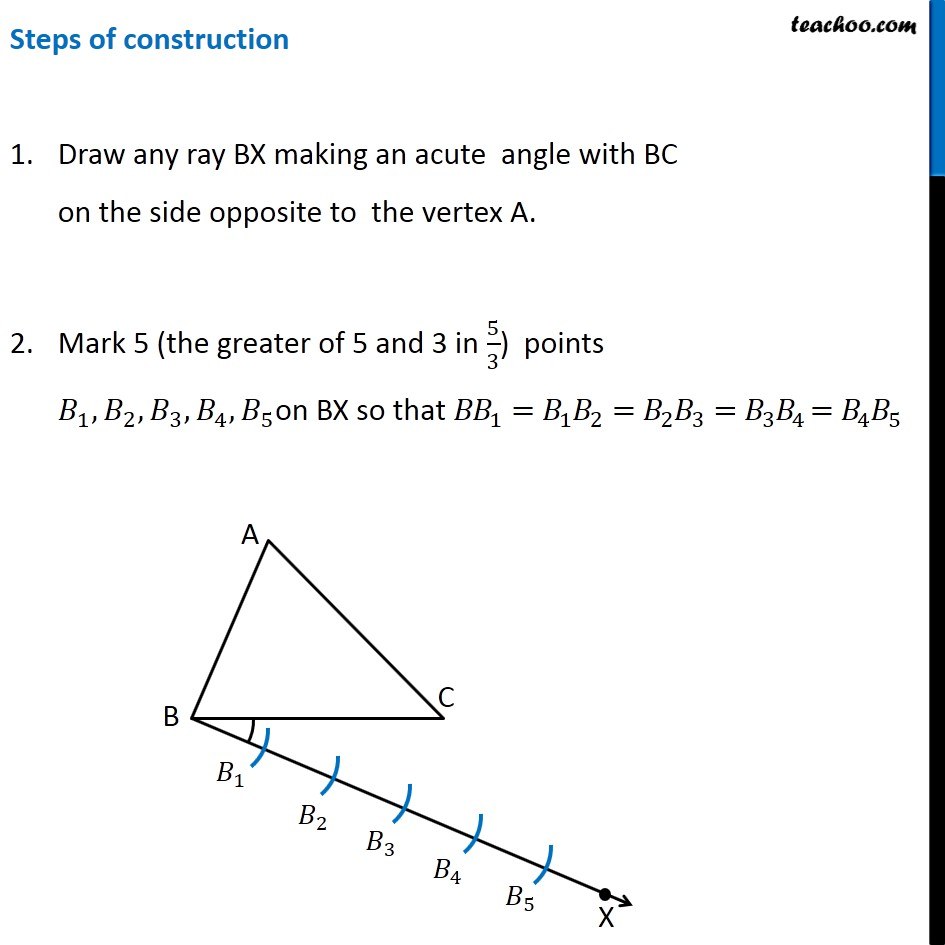
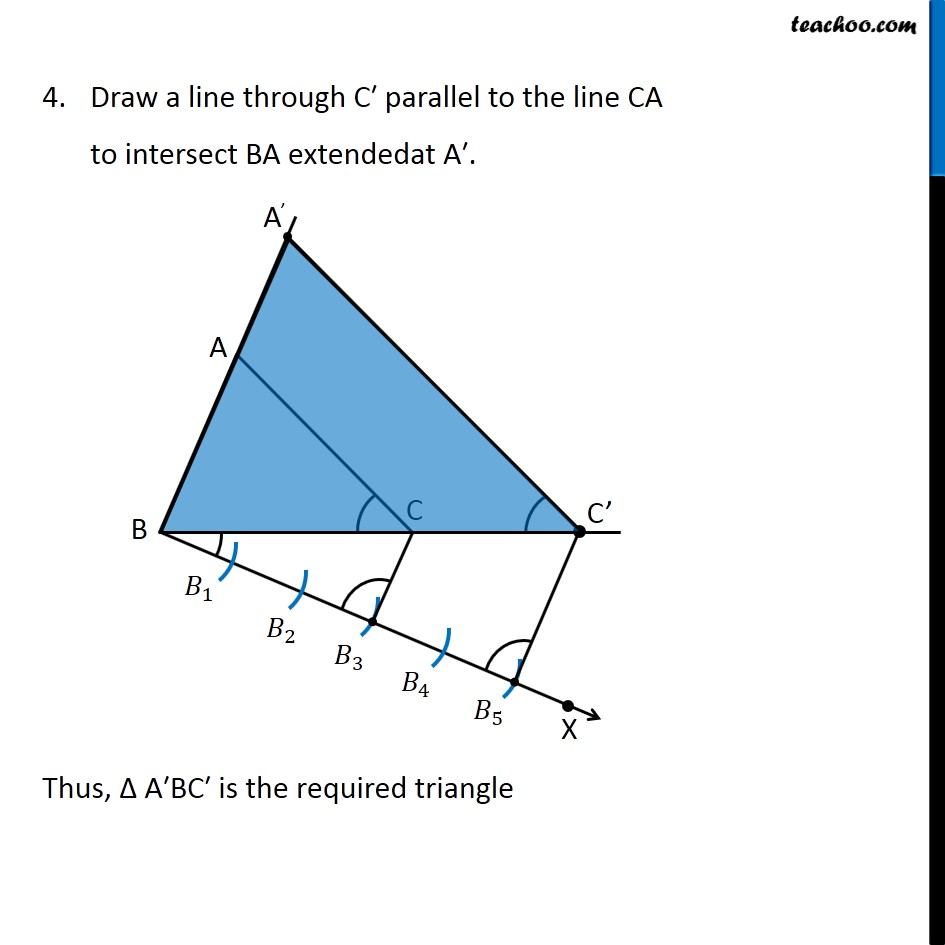
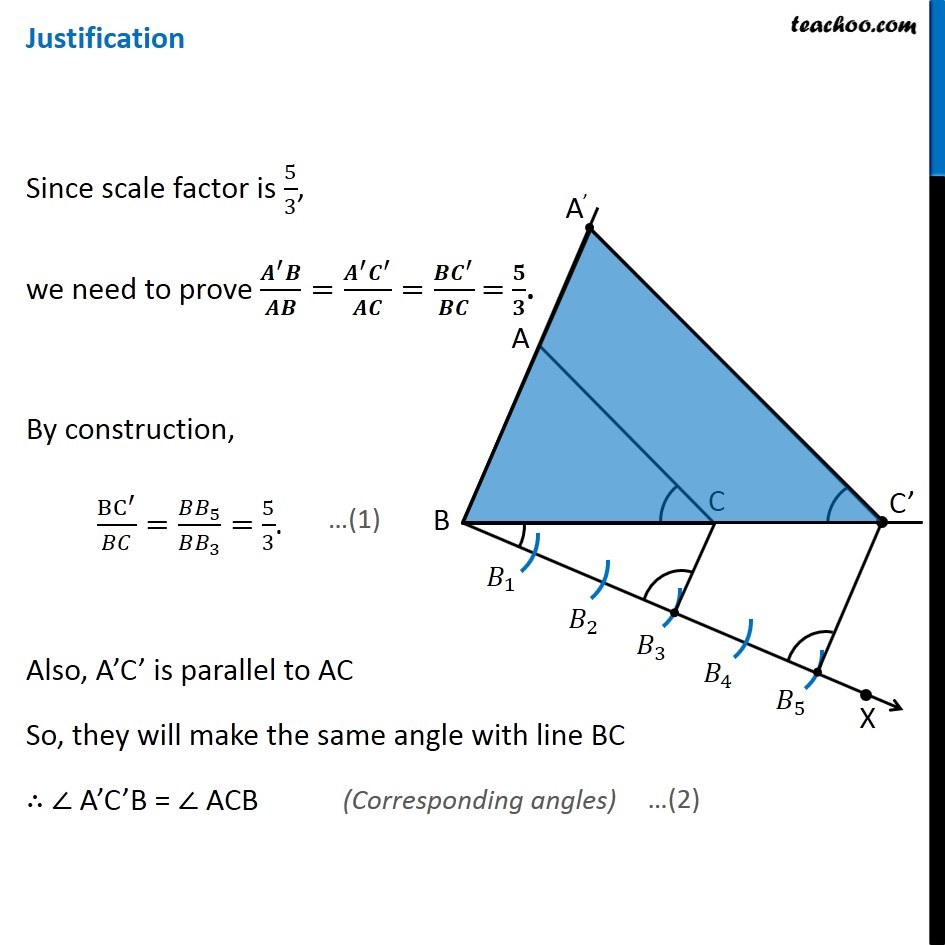
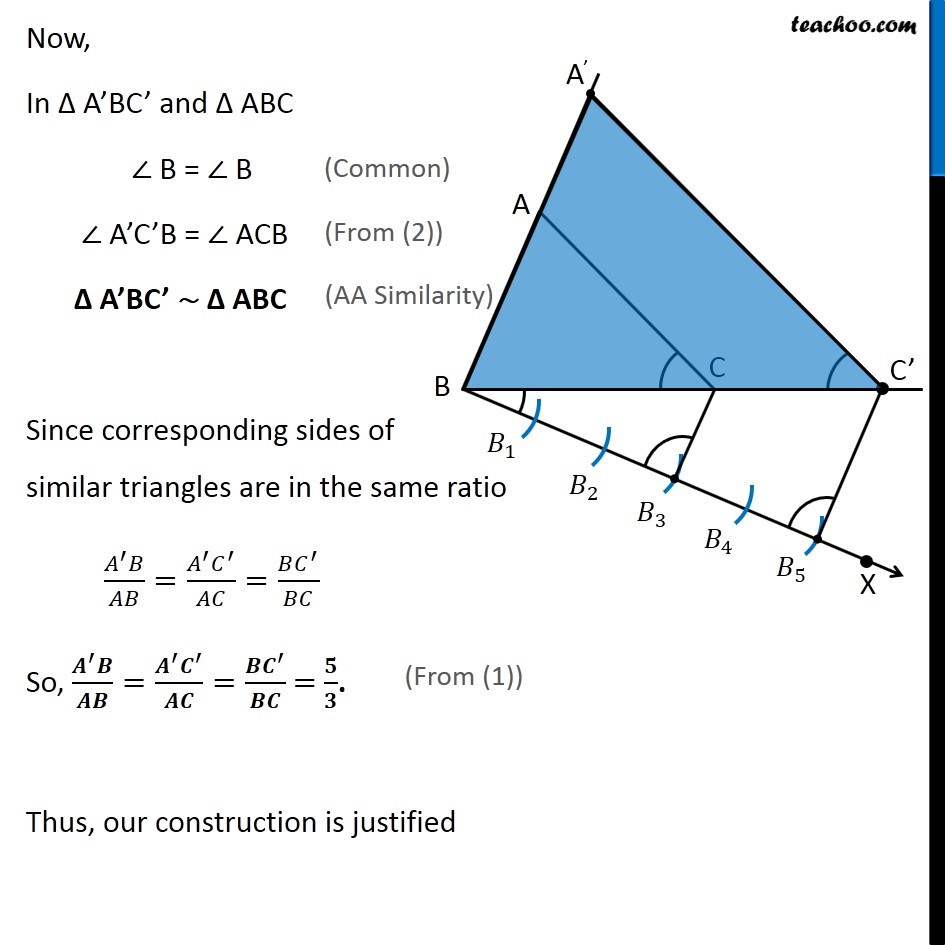
Example 2 Construct a triangle similar to a given triangle ABC with its sides equal its to 5/3 of the corresponding sides of the triangle ABC (scale factor 5/3). Here, we are given Δ ABC, and scale factor 5/3 ∴ Scale Factor > 1 We need to construct triangle similar to Δ ABC Let’s follow these steps Steps of construction Draw any ray BX making an acute angle with BC on the side opposite to the vertex A. Mark 5 (the greater of 5 and 3 in 5/3) points 𝐵_1,𝐵_2,𝐵_3,𝐵_4,𝐵_5on BX so that 〖𝐵𝐵〗_1=𝐵_1 𝐵_2=𝐵_2 𝐵_3=𝐵_3 𝐵_4 =𝐵_4 𝐵_5 Join 𝐵_3C (3rd point as 3 is smaller in 5/3) and draw a line through 𝐵_5 parallel to 𝐵_3 𝐶, to intersect BC extended at C′. Draw a line through C′ parallel to the line CA to intersect BA extendedat A′. Thus, Δ A′BC′ is the required triangle Justification Since scale factor is 5/3, we need to prove (𝑨^′ 𝑩)/𝑨𝑩=(𝑨^′ 𝑪^′)/𝑨𝑪=(𝑩𝑪^′)/𝑩𝑪 = 𝟓/𝟑. By construction, BC^′/𝐵𝐶=(𝐵𝐵_5)/(𝐵𝐵_3 )= 5/3. Also, A’C’ is parallel to AC So, they will make the same angle with line BC ∴ ∠ A’C’B = ∠ ACB Justification Since scale factor is 5/3, we need to prove (𝑨^′ 𝑩)/𝑨𝑩=(𝑨^′ 𝑪^′)/𝑨𝑪=(𝑩𝑪^′)/𝑩𝑪 = 𝟓/𝟑. By construction, BC^′/𝐵𝐶=(𝐵𝐵_5)/(𝐵𝐵_3 )= 5/3. Also, A’C’ is parallel to AC So, they will make the same angle with line BC ∴ ∠ A’C’B = ∠ ACB (Corresponding angles) Now, In Δ A’BC’ and Δ ABC ∠ B = ∠ B (Common) ∠ A’C’B = ∠ ACB (From (2)) Δ A’BC’ ∼ Δ ABC (AA Similarity) Since corresponding sides of similar triangles are in the same ratio (𝐴^′ 𝐵)/𝐴𝐵=(𝐴^′ 𝐶^′)/𝐴𝐶=(𝐵𝐶^′)/𝐵𝐶 So, (𝑨^′ 𝑩)/𝑨𝑩=(𝑨^′ 𝑪^′)/𝑨𝑪=(𝑩𝑪^′)/𝑩𝑪 = 𝟓/𝟑. (From (1)) Thus, our construction is justified