Question 1 - Constrcting Line Segment in a given ratio and Similar Triangles - Constructions

Transcript

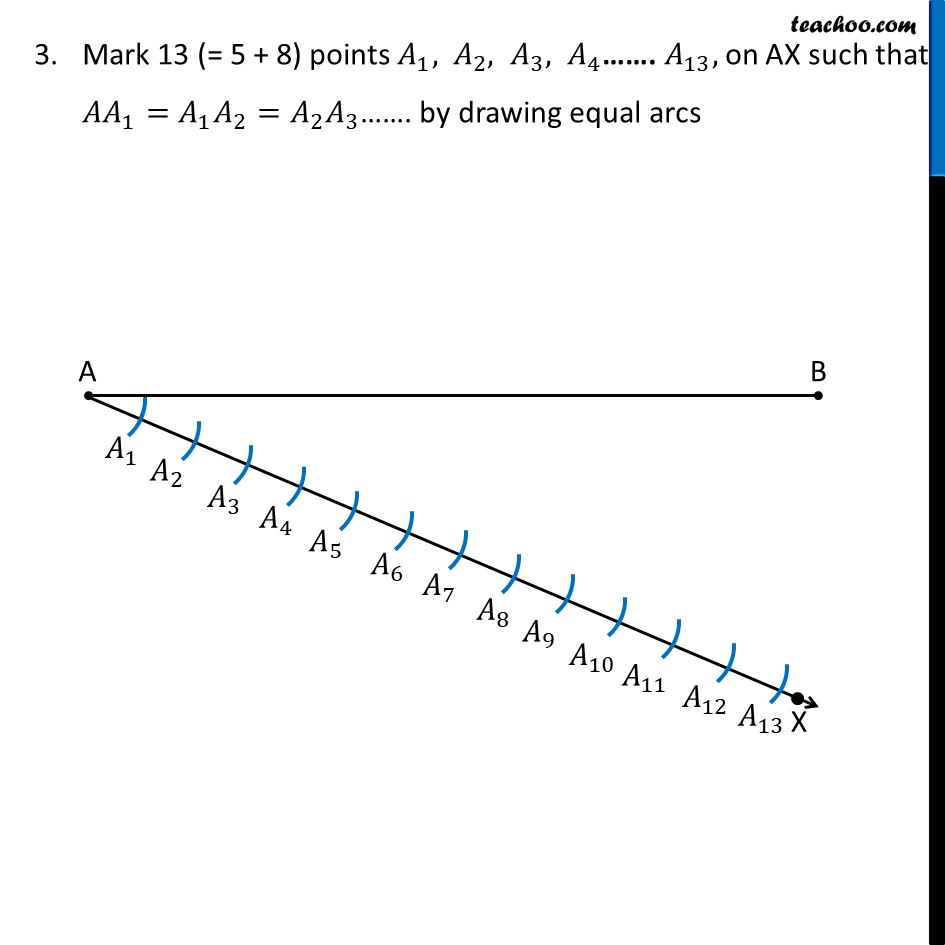
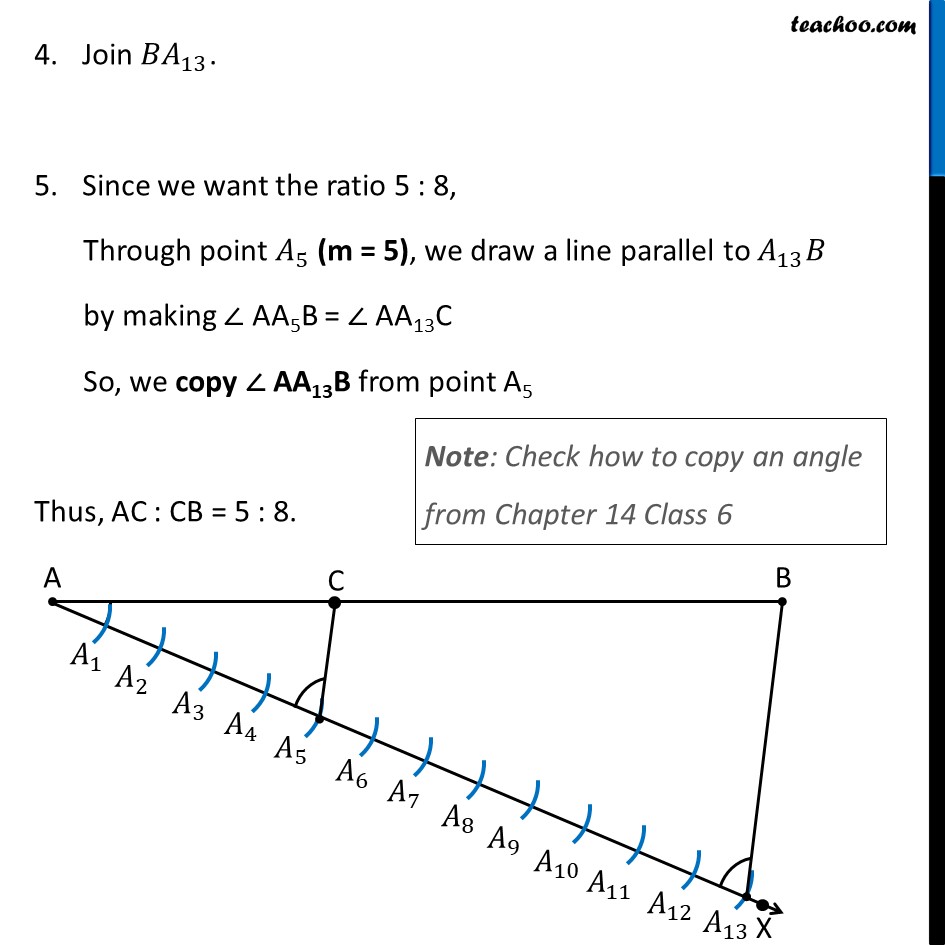
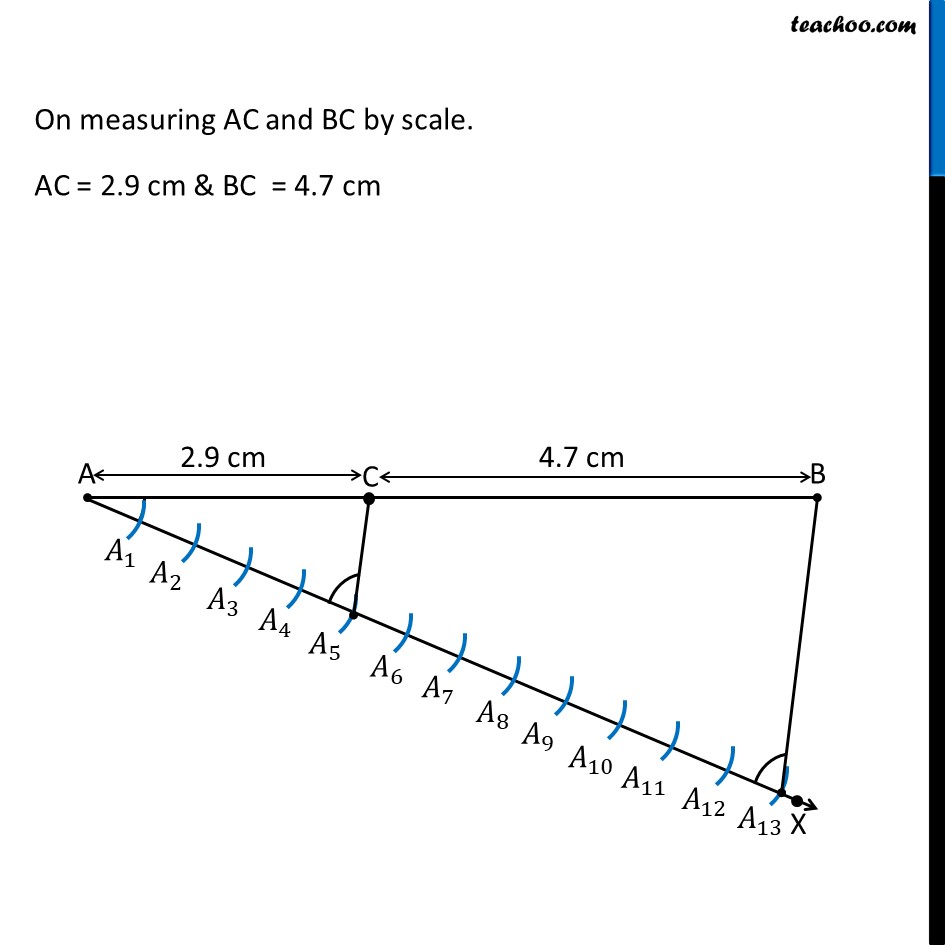
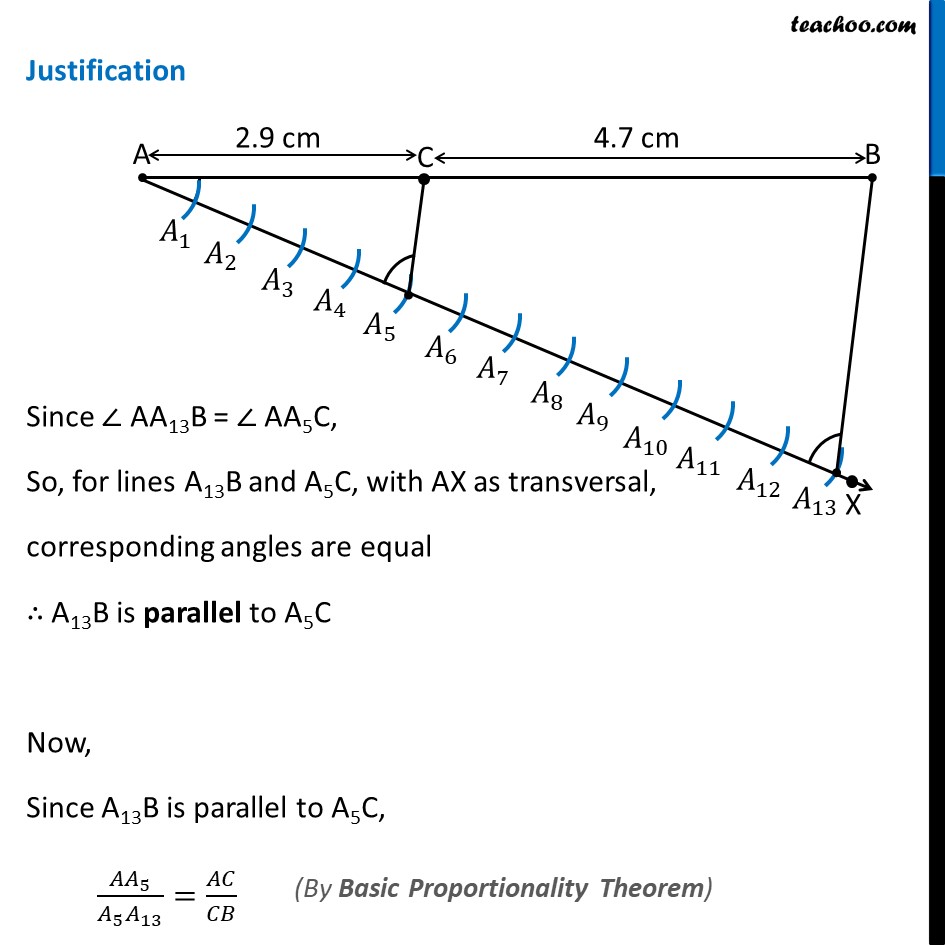
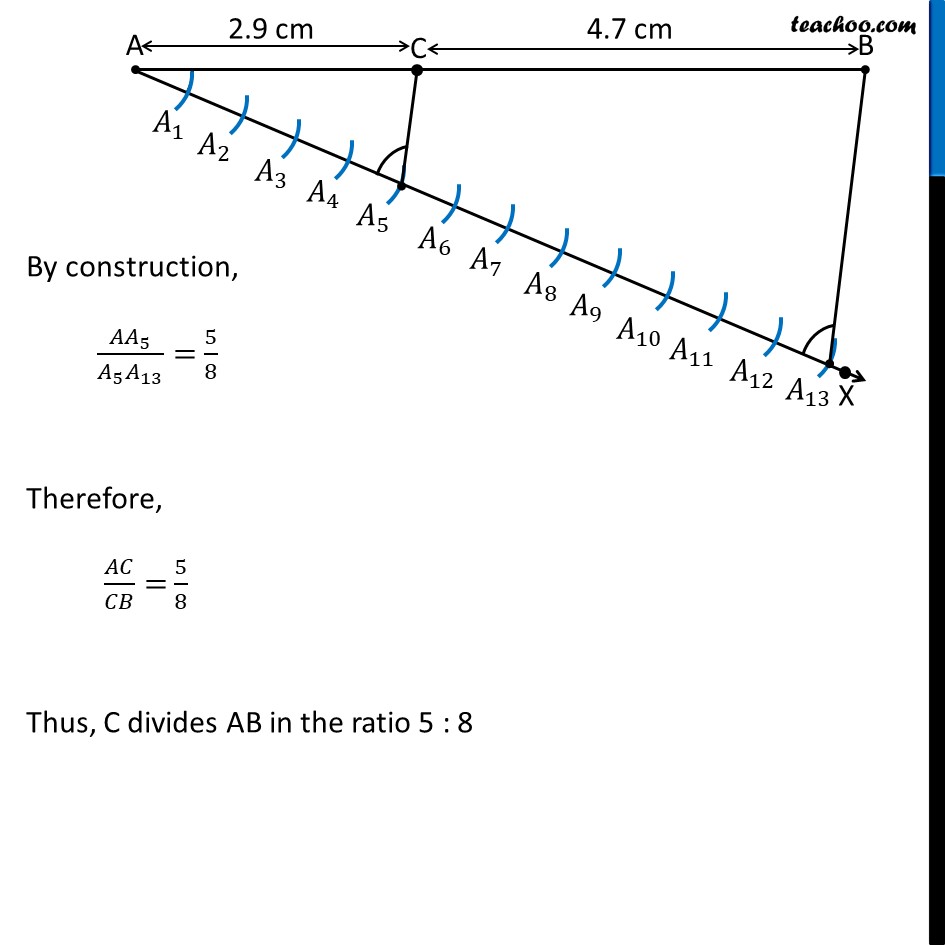
Question 1 Draw a line segment length 7.6 cm and divide it in the ratio 5 : 8. Measure the two parts. Give the justification of the construction. Steps of construction: Draw line segment AB of length 7.6 cm Draw any ray AX, making an acute angle with AB. Mark 13 (= 5 + 8) points 𝐴_1, 〖 𝐴〗_2, 𝐴_3, 𝐴_4……. 𝐴_13, on AX such that 〖𝐴𝐴〗_1=𝐴_1 𝐴_2=𝐴_2 𝐴_3……. by drawing equal arcs Join 〖𝐵𝐴〗_13. Since we want the ratio 5 : 8, Through point 𝐴_5 (m = 5), we draw a line parallel to 𝐴_13 𝐵 by making ∠ AA5B = ∠ AA13C So, we copy ∠ AA13B from point A5 Note: Check how to copy an angle from Chapter 14 Class 6 Thus, AC : CB = 5 : 8. On measuring AC and BC by scale. AC = 2.9 cm & BC = 4.7 cm Justification Since ∠ AA13B = ∠ AA5C, So, for lines A13B and A5C, with AX as transversal, corresponding angles are equal ∴ A13B is parallel to A5C Now, Since A13B is parallel to A5C, 〖𝐴𝐴〗_5/(𝐴_5 𝐴_13 )=𝐴𝐶/𝐶𝐵 (By Basic Proportionality Theorem) By construction, 〖𝐴𝐴〗_5/(𝐴_5 𝐴_13 )= 5/8 Therefore, 𝐴𝐶/𝐶𝐵= 5/8 Thus, C divides AB in the ratio 5 : 8