You are here
Misc 11 (MCQ) - Chapter 13 Class 12 Probability
Last updated at Dec. 16, 2024 by Teachoo
Chapter 13 Class 12 Probability
Concept wise
-
Conditional Probability - Values given
- Conditional Probability - Statement
- Multiplication rule of probability
- Independent events
- Basic Probability
- Theorem of total probability
- Bayes theorem
- Random Variable - Defination
- Probability distribution
- Mean or Expectation of random variable
- Variance and Standard Deviation of a Random Variable
- Bernoulli Trials
- Binomial Distribution
Transcript
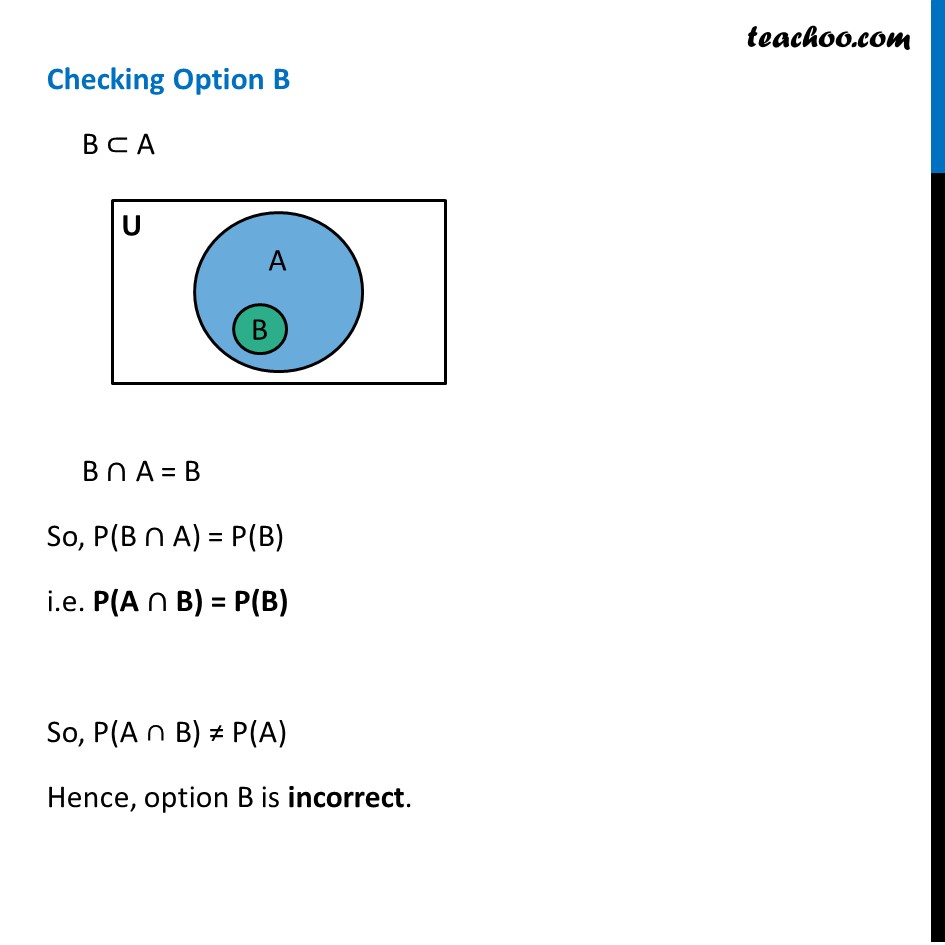
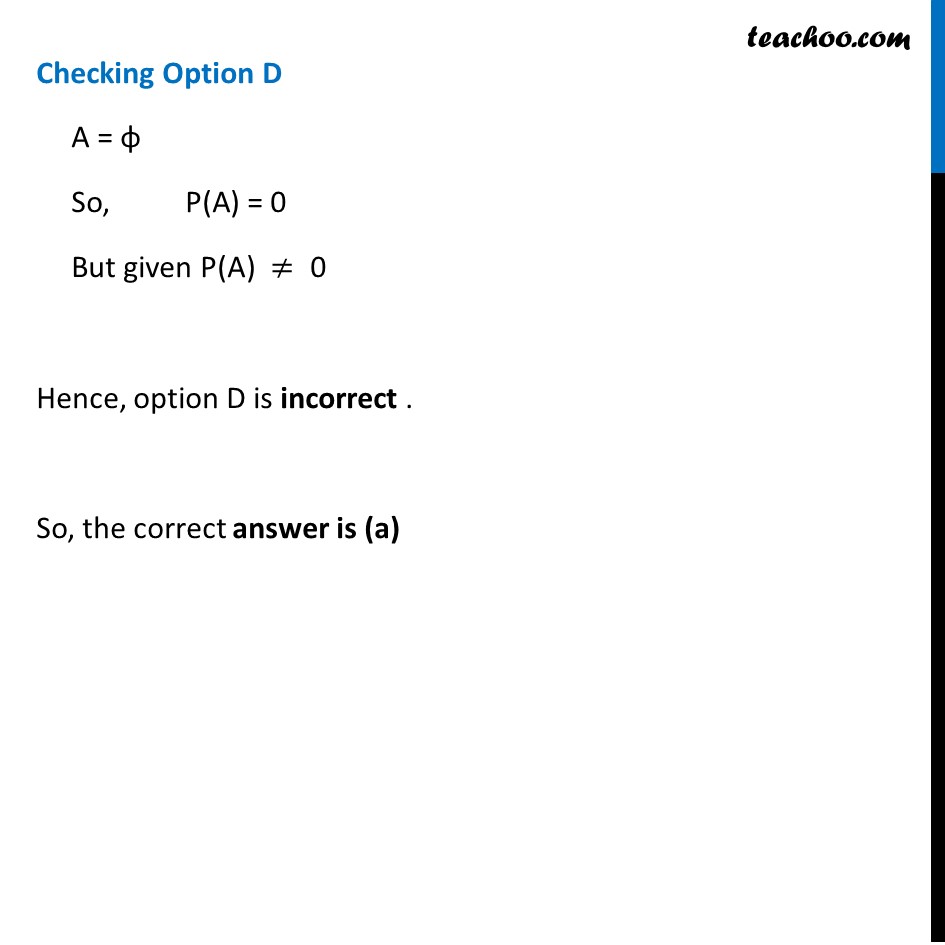
Misc 11 If A and B are two events such that P(A) ≠ 0 and P(B|A) = 1, then (A) A ⊂ B (B) B ⊂ A (C) B = φ (D) A = φ Given P(B|A) = 1 i.e. (𝑃(𝐴 ∩ 𝐵))/(𝑃(𝐴))=1 𝑷(𝑨∩𝑩)=𝑷(𝑨) Checking Option A A ⊂ B ∴ A∩B=A So, P(A∩B)=P(A) Hence, Option A is correct. Checking Option B B ⊂ A B ∩ A = B So, P(B ∩ A) = P(B) i.e. P(A ∩ B) = P(B) So, P(A ∩ B) ≠ P(A) Hence, option B is incorrect. Checking Option C B = φ P(B) = 0 So, P(A) = 1 Since, B = φ ∴ P(A ∩ B) = 0 So, P(A ∩ B) ≠ P(A) Hence, option C is Incorrect. Checking Option D A = φ So, "P(A) = 0" But given "P(A) "≠" 0" Hence, option D is incorrect . So, the correct answer is (a)
