Question 13 - Probability Distribution - Chapter 13 Class 12 Probability

Transcript

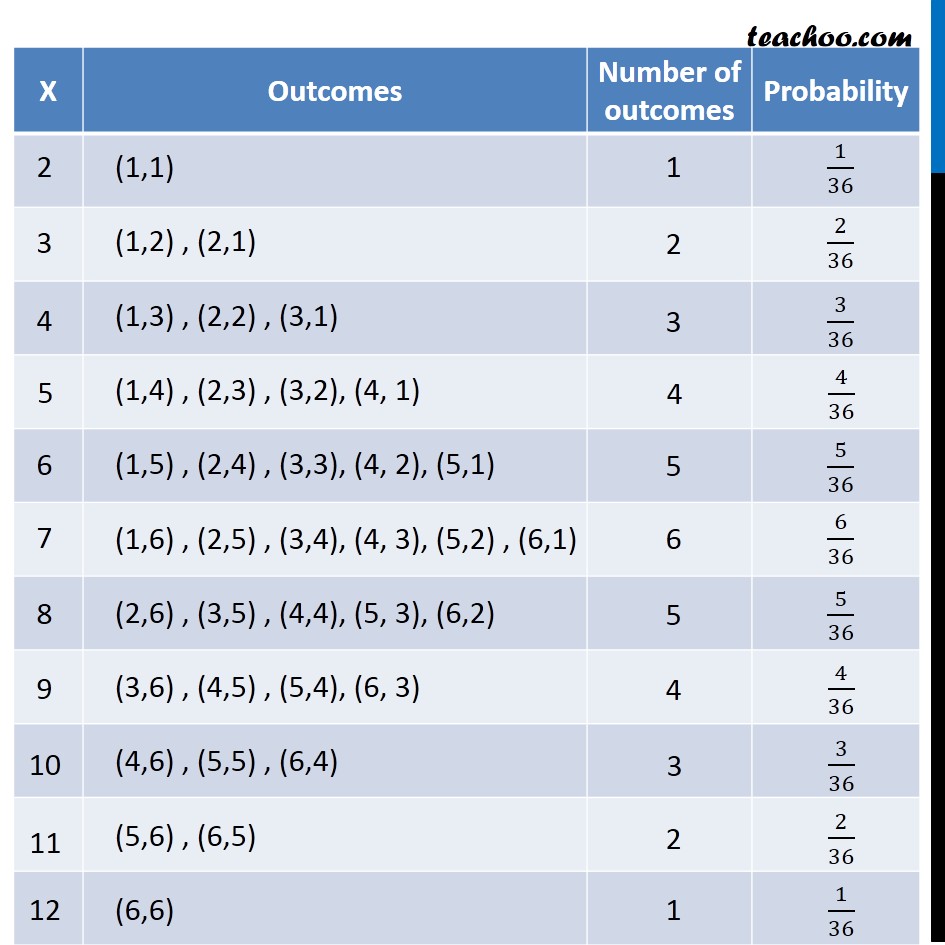
Question 13 Let X denote the sum of the numbers obtained when two fair dice are rolled. Find the variance and standard deviation of X.Question 13 Let X denote the sum of the numbers obtained when two fair dice are rolled. Find the variance and standard deviation of X.Thus, Probability distribution is Now, we need to find variance Var (𝑋) "= " 𝐸(𝑋^2 )−[𝐸(𝑋)]^2 Finding E(X) E(X) = ∑_(𝑖 = 1)^𝑛▒𝑥𝑖𝑝𝑖 = 2 ×1/36+3 × 2/36+4 × 3/36+5 ×4/36+6 × 5/36+7 × 6/36 +8 × 5/36+9 × 4/36+10 ×3/36+11 × 2/36+12 × 1/36 = (2 + 6 + 12 + 20 + 30 + 42 + 40 + 36 + 30 + 22 + 12)/36 = (252 )/36 = 7 Thus E(x) = 7 Finding E(𝑿^𝟐 ) E(𝑿^𝟐 )=∑_(𝑖=1)^𝑛▒〖𝑥^2 𝑖𝑃𝑖〗 = 2^2×1/36 +3^2×2/36 +4^2 ×3/36+5^2×4/36+6^2×5/36+7^2× 6/36 +8^2 ×5/36+9^2× 4/36+〖10〗^2×3/36+〖11〗^2 ×2/36+〖12〗^2×1/36 = (4 + 18 + 48 + 100 + 180 + 294 + 320 + 324 + 300 + 242 + 144)/36 = 1974/36 = 𝟑𝟐𝟗/𝟔 Now, Var (𝑿) "= " 𝑬(𝑿^𝟐 )−[𝑬(𝑿)]^𝟐 = 329/6−(7)^2 = (329 − 6 × 49)/6 = 35/6 = 5.833 Standard deviation is given by 𝝈_𝒙=√(𝒗𝒂𝒓 (𝑿) ) =√(35/6) =√5.833 = 2.415 43 × 3 = 129 44 × 4 = 176 45 × 5 = 225 4824 × 4 = 19296 4825 × 5 = 24125 4826 × 6 = 28956