Introducing your new favourite teacher - Teachoo Black, at only ₹83 per month
Ex 13.1, 11 - Chapter 13 Class 12 Probability (Term 2)
Last updated at July 16, 2021 by Teachoo
Conditional Probability - Statement
Chapter 13 Class 12 Probability
Concept wise
- Conditional Probability - Values given
-
Conditional Probability - Statement
- Multiplication rule of probability
- Independent events
- Basic Probability
- Theorem of total probability
- Bayes theorem
- Random Variable - Defination
- Probability distribution
- Mean or Expectation of random variable
- Variance and Standard Deviation of a Random Variable
- Bernoulli Trials
- Binomial Distribution
Transcript
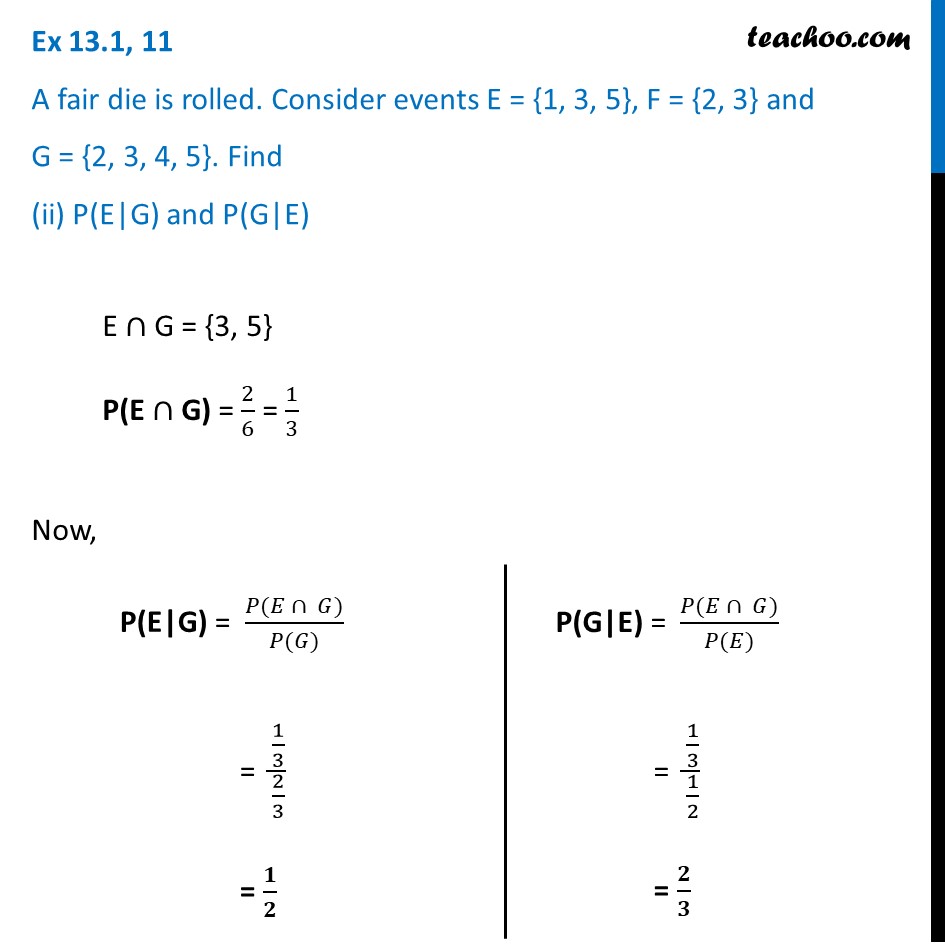
Ex 13.1, 11 A fair die is rolled. Consider events E = {1,3,5}, F = {2,3} and G = {2,3,4,5} Find (i) P(E|F) and P (F|E) A fair die is rolled S = {1, 2, 3, 4, 5, 6} Given, E = {1, 3, 5} P(E) = 36 = 12 F = {2, 3} P(F) = 26 = 13 & G = {2, 3, 4, 5} P(G) = 46 = 23 We need to find P(E|F) and P(F|E) Now, E∩F = {3} P(E∩F) = 16 Now, Ex 13.1, 11 A fair die is rolled. Consider events E = {1,3,5}, F = {2,3} and G = {2,3,4,5} Find (ii) P(E|G) and P(G|E) E∩G = {3, 5} P(E∩G) = 26 = 13 Now, Ex 13.1, 11 A fair die is rolled. Consider events E = {1,3,5}, F = {2,3} and G = {2,3,4,5} Find (iii) P((E ∪ F)|G) and P((E ∩ F)|G)
