Question 8 - Whether binary commutative/associative or not - Chapter 1 Class 12 Relation and Functions

Transcript

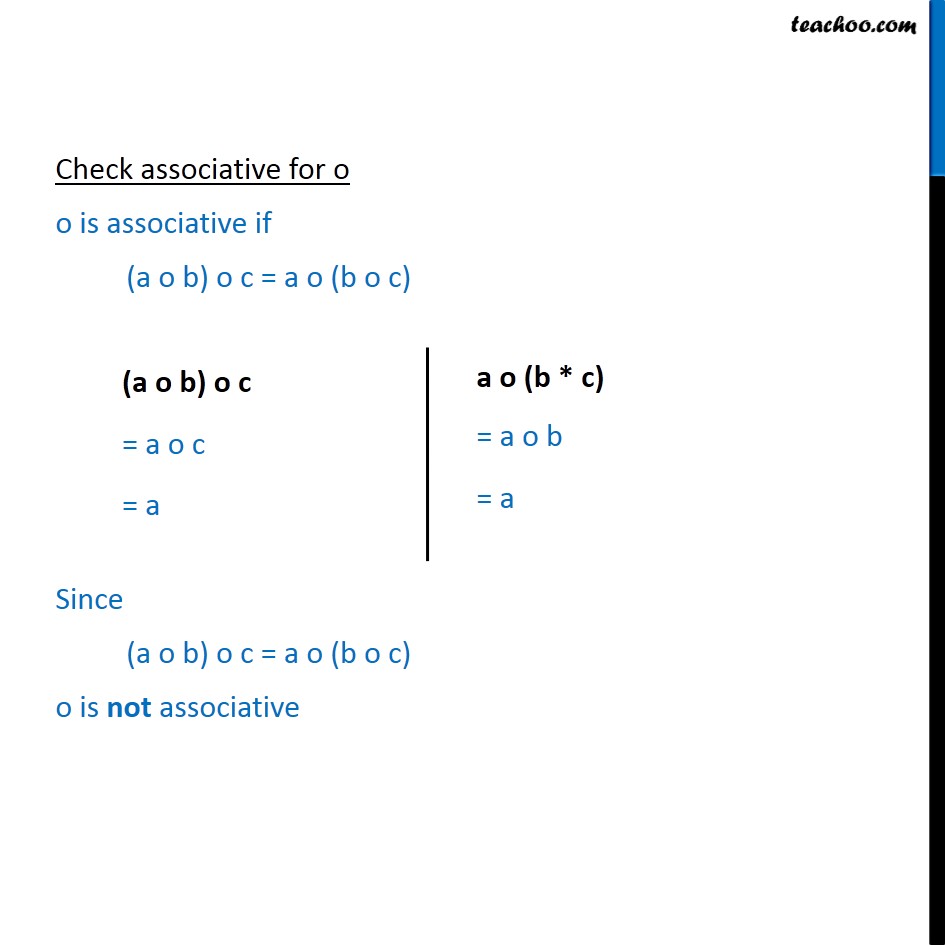
Question 8 Consider the binary operations * : R × R → and o : R × R → R defined as a * b = a – b﷯ and a o b= a, ∀ a, b ∈ R. Show that * is commutative but not associative, o is associative but not commutative. Further, show that ∀ a, b, c ∈ R, a * (b o c) = (a * b) o (a * c). (If it is so, we say that the operation * distributes over the operation o). Does o distribute over *? Justify your answer. Check commutative for * * is commutative if a * b = b * a Since a * b = b * a ∀ a, b ∈ R * is commutative Check associative for * * is associative if (a * b) * c = a * (b * c) Since (a * b) * c ≠ a * (b * c) * is not associative a o b = a Check commutative for o o is commutative if a o b = b o a Since a o b ≠ b o a * is not commutative Check associative for o o is associative if (a o b) o c = a o (b o c) Since (a o b) o c = a o (b o c) o is not associative a * b = a – b﷯ & a o b = a * distributes over o If a * (b o c) = (a * b) o (a * c), ∀ a, b, c ∈ R * distributes over o Since a * (b o c) = (a * b) o (a * c), ∀ a, b, c ∈ R * distributes over o a * b = a – b﷯ & a o b = a o distributes over * If a o (b * c) = (a o b) * (a o c), ∀ a, b, c ∈ R o distributes over * Since a o (b * c) ≠ (a o b) * (a o c) o does not distributes over *