Question 2 - Figure it out (Page 263) - Hollow Integer Grid - Chapter 10 Class 6 - The other side of Zero (Ganita Prakash)

Transcript

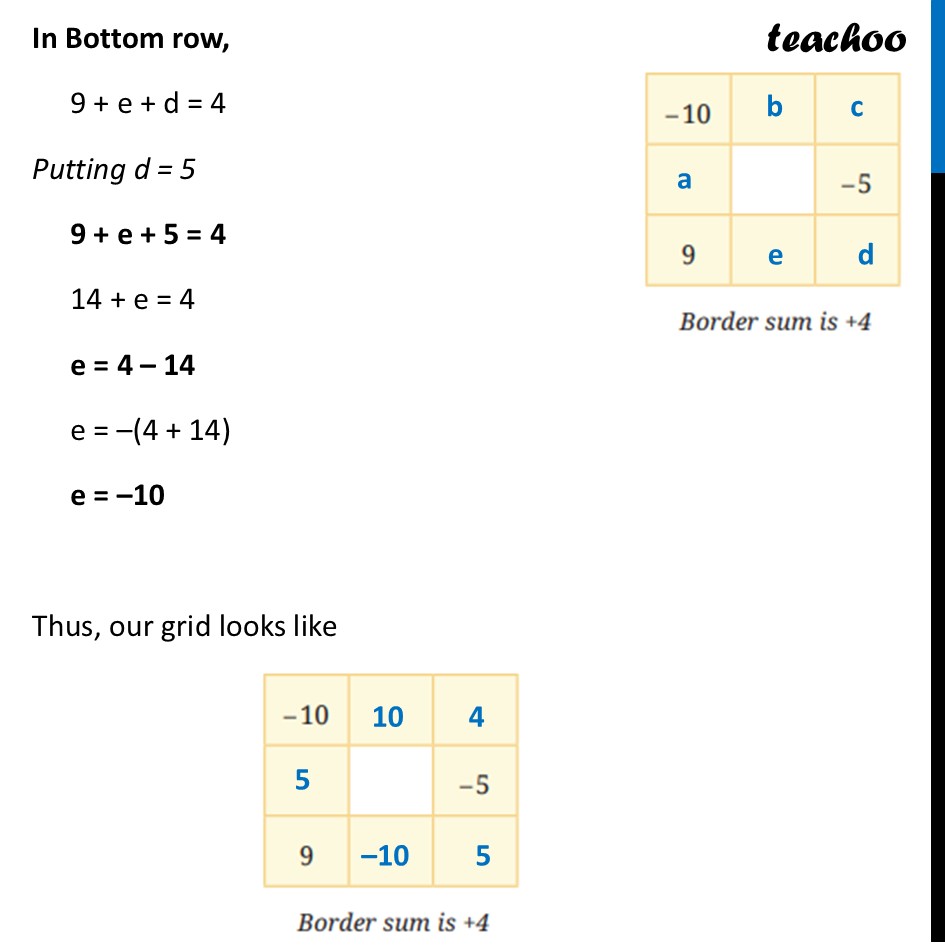
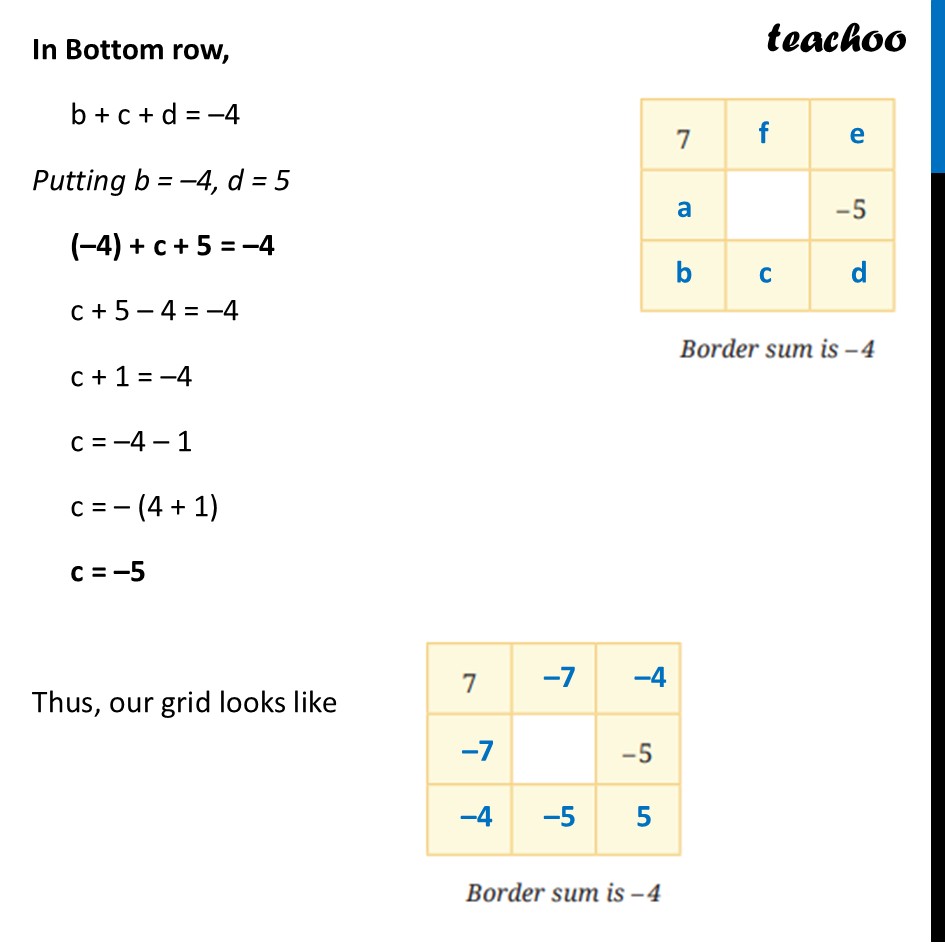
Question 2 - Figure it out (Page 264) Complete the grids to make the required border sum:Let’s solve this one by one Grid 1Let us name the remaining numbers Given Border sum is +4 Now, Sum of left column = (–10) + a + 9 = 4 Solving (–10) + a + 9 = 4 a – 10 + 9 = 4 a – (10 – 9) = 4 a – 1 = 4 a = 4 + 1 a = 5 For other rows or columns, we can put any value to get Border sum 4 In Top row, Let b = +10, so we can make –10 + 10 = 0 Then, c = +4 In Left column, Since c = 4, we can make d = +5, so we can make –5 + 5 = 0 In Bottom row, 9 + e + d = 4 Putting d = 5 9 + e + 5 = 4 14 + e = 4 e = 4 – 14 e = –(4 + 14) e = –10 Grid 2Let us name the remaining numbers Given Border sum is (–2) Now, Sum of top row = 6 + 8 + d = (–2) Solving 6 + 8 + d = (–2) 14 + d = –2 d = –2 – 14 Taking – common d = – (2 + 14) d = –16 For other rows or columns, we can put any value to get Border sum (–2) In Left column, Let a = –6, so we can make 6 – 6 = 0 Then, b = –2 In Right column, d + (–5) + c = –2 Putting d = –16 (–16) + (–5) + c = –2 –(16 + 5) + c = –2 –21 + c = –2 c = –2 + 21 c = 21 – 2 c = 19 Thus, our grid looks like Grid 3Let us name the remaining numbers Given Border sum is (–4) For all the rows or columns, we can put any value to get Border sum (–4) In Left column, Let a = –7, so we can make 7 – 7 = 0 Then, b = –4 In Top row, Let f = –7, so we can make 7 – 7 = 0 Then, e = –4 In Right column, e + (–5) + d = –4 Putting e = –4 (–4) + (–5) + d = –4 –(4 + 5) + d = –4 –9 + d = –4 d = –4 + 9 d = 9 – 4 d = 5 In Bottom row, b + c + d = –4 Putting b = –4, d = 5 (–4) + c + 5 = –4 c + 5 – 4 = –4 c + 1 = –4 c = –4 – 1 c = – (4 + 1) c = –5 Thus, our grid looks like Thus, our grid looks like