Example 3 - Chapter 13 Class 10 Statistics

Transcript

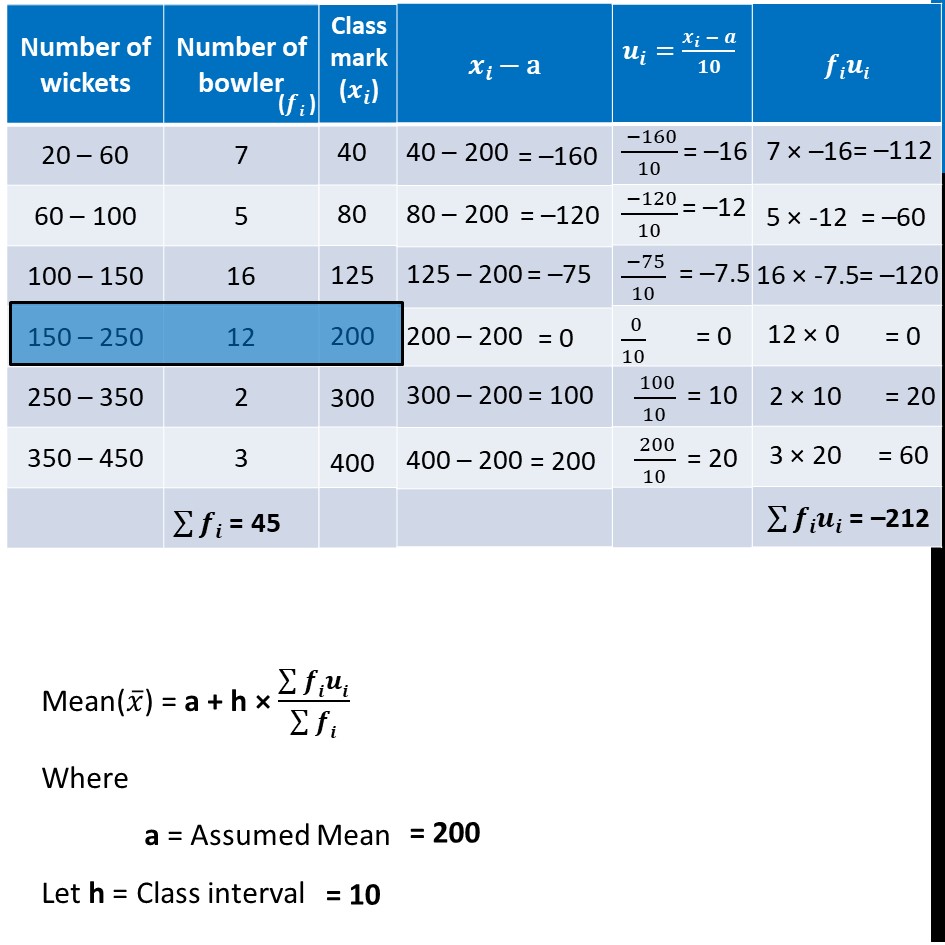
Example 3 (Method 1 – Direct Method) The distribution below shows the number of wickets taken by bowlers in one-day cricket matches. Find the mean number of wickets by choosing a suitable method. What does the mean signify? Here Class Size is not same, So, we solve by Direct Method Mean(𝑥 ̅) = (∑▒𝑓𝑖𝑥𝑖)/(∑▒𝑓𝑖) 𝑥 ̅ = 6880/45 𝑥 ̅ = 152.89 Thus, Mean signifies that on average, 45 bowlers take 152.89 wickets Example 3 (Method 2 – Step Deviation Method) The distribution below shows the number of wickets taken by bowlers in one-day cricket matches. Find the mean number of wickets by choosing a suitable method. What does the mean signify? Here Class Size is not same… So, in Step Deviation Method Mean(𝑥 ̅) = a + h × (∑▒𝒇𝒊𝒖𝒊)/(∑▒𝒇𝒊) We use a value of h which can divide 𝑑𝑖 = 𝑥𝑖 − a Mean(𝑥 ̅) = a + h × (∑▒𝒇𝒊𝒖𝒊)/(∑▒𝒇𝒊) Where a = Assumed Mean Let h = Class interval Also, ∑▒𝒇𝒊 = 45 ∑▒𝒇𝒊𝒖𝒊 = −212 Putting values in formula Mean(𝒙 ̅) = a + h × (∑▒𝒇𝒊𝒖𝒊)/(∑▒𝒇𝒊) 𝑥 ̅ = 200 + 10 × (−212)/45 𝑥 ̅ = 200 – 47.11 𝒙 ̅ = 152.89 Thus, Mean signifies that on average, 45 bowlers take 152.89 wickets