Question 5 - Frustum - Area and Volume - Chapter 12 Class 10 Surface Areas and Volumes

Transcript

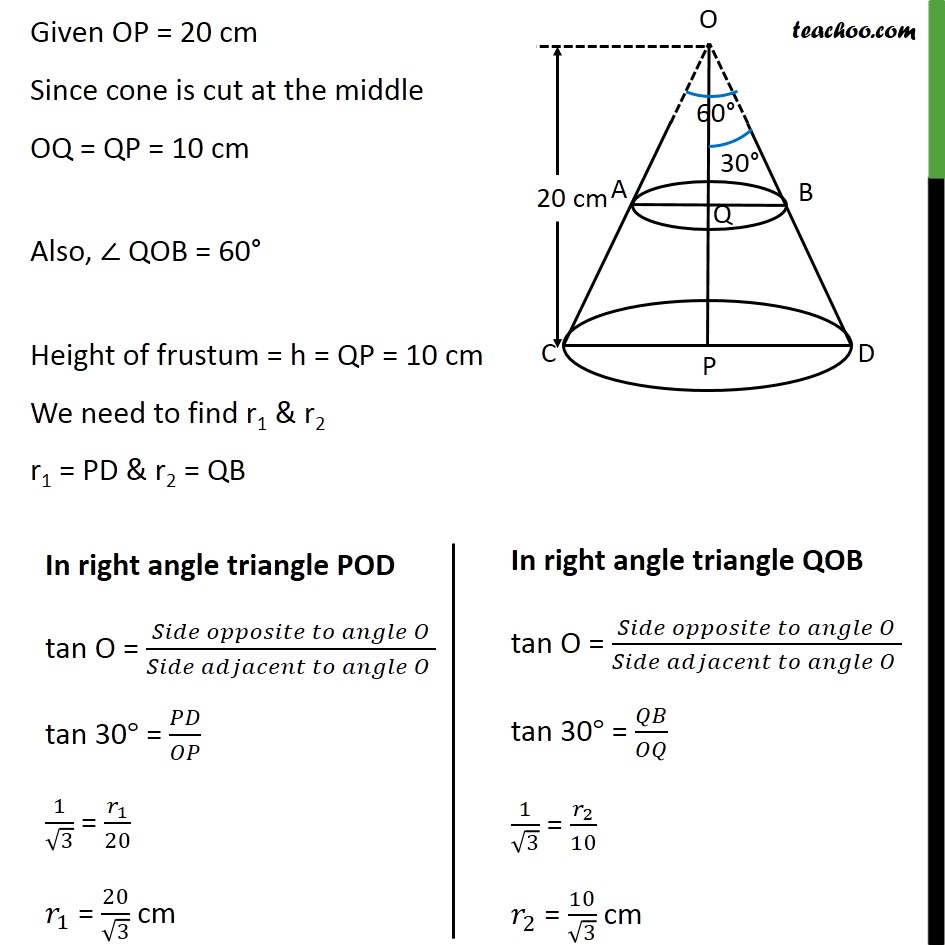
Question 5 A metallic right circular cone 20 cm high and whose vertical angle is 60 is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter 1/16 cm ,find the length of the wire. Let OCD be the metallic cone and ABDC be the required frustum Since frustum is drawn into wire Volume of frustum ABDC = Volume of cylindrical wire Volume of frustum ABDC Volume of frustum = /3( 12+ 22+ 1 2) Given OP = 20 cm Since cone is cut at the middle OQ = QP = 10 cm Also, QOB = 60 Height of frustum = h = QP = 10 cm We need to find r1 & r2 r1 = PD & r2 = QB Now , Volume of the frustum ADBC = /3( 12+ 22+ 1 2) = ( 10)/3 (( 20/ 3)^2 +( 10/ 3)^2+20/ 3 10/ 3) = 10 /3 (400/3+100/3+200/3) = 10 /3 (700/3) = 7000 /9 cm3 Volume of cylindrical wire Given diameter = 1/16 cm Radius = r = (1/16)/2 = 1/(16 2) = 1/32 cm Let length of wire = height of cylinder = h cm Volume of wire = 2 = (1/32)^2 = /(32 32) Now, Volume of the frustum = volume of wire 7000 /9 = /(32 32) (7000 32 32)/(9 ) = h h = (7000 32 32)/(9 ) h = 796444.44 cm h = 796444.44/100 m h = 7964.4 m Hence, length of wire = h = 7964.4 m