Question 15 - Chapter 12 Class 10 Areas related to Circles (Important Question)

Transcript

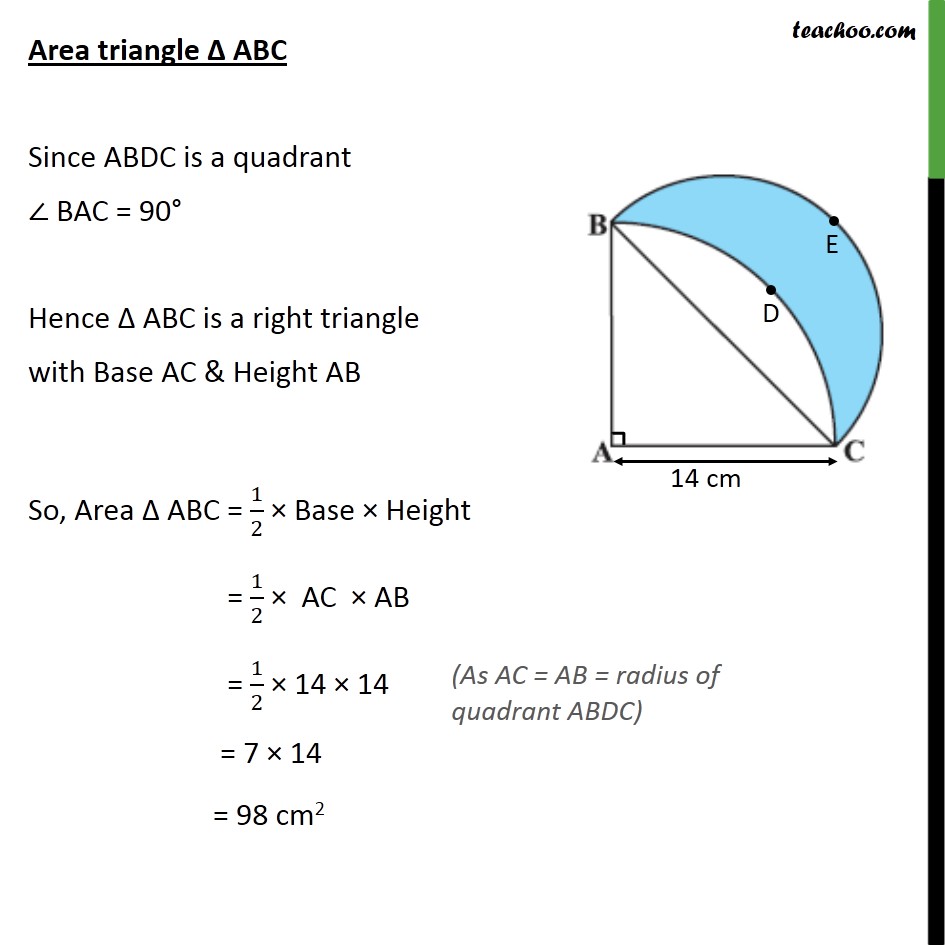
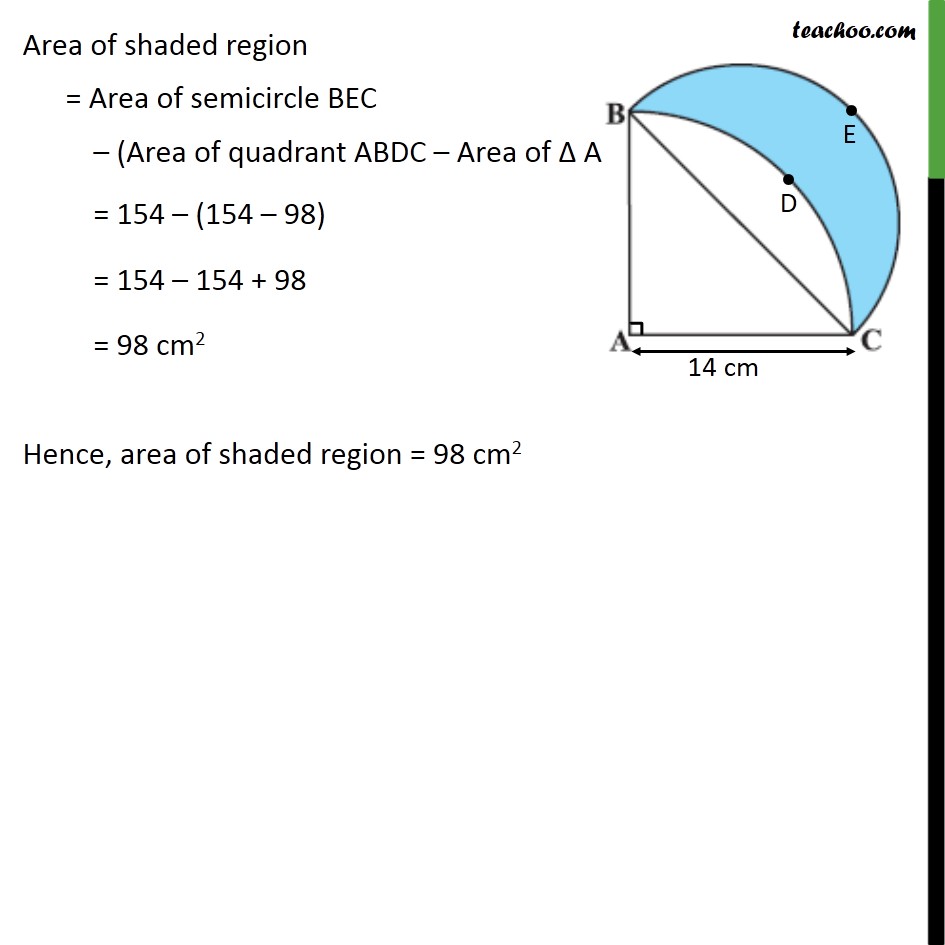
Question 15 In figure, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region. Area of shaded region = Area of semicircle BEC (Area of quadrant ABDC Area of ABC) Area quadrant ABDC Radius = 14 cm Area of quadrant ABDC = 1/4 (area of circle) = 1/4 ( r2) = 1/4 22/7 (14)^2 = 1/4 22/7 14 14 = 154 cm2 Area triangle ABC Since ABDC is a quadrant BAC = 90 Hence ABC is a right triangle with Base AC & Height AB So, Area ABC = 1/2 Base Height = 1/2 AC AB = 1/2 14 14 = 7 14 = 98 cm2 Area semicircle BEC Here, Diameter = BC Finding BC first Since ABC is a right triangle Applying Pythagoras theorem in right triangle ABC (Hypotenuse)2 = (Height)2 + (Base)2 (BC)2 = (AB)2 + (AC)2 (BC)2 = (14)2 + (14)2 (BC)2 = (14)2 2 BC = ("(14)2 2" ) BC = ("(14)2" ) ("2" ) BC = 14 ("2" ) BC = 14 2 cm So, Diameter = BC = 14 2 cm Radius = r = /2 = /2 = (14 2)/2 = 7 2 cm Area of semicircle BEC = 1/2 Area of circle = 1/2 ( 2) = 1/2 22/7 (7 2)^2 = 1/2 22/7 7 7 2 2 = 1/2 22 7 2 = 154 cm2 Area of semi circle BEC = 154 cm2 Area of shaded region = Area of semicircle BEC (Area of quadrant ABDC Area of ABC) = 154 (154 98) = 154 154 + 98 = 98 cm2 Hence, area of shaded region = 98 cm2